[Fundamental of Power Electronics]-PART I-6.变换器电路-6.3 变压器隔离

6.3 变压器隔离

在许多应用场合中，期望将变压器结合到开关变换器中，从而在变换器的输入输出之间形成直流隔离。例如，在离线(off-line)应用中（变换器输入连接到交流公用系统），根据监管部门要求，需要隔离。在这些情况下，只需要在变换器的交流输入端连接一个50Hz或者60Hz的变压器即可获得隔离。但由于变压器的尺寸和重量随频率成反比，因此通过将变压器并入变换器中恶意实现显著的改进， 使得变压器以数十或者百KHz频率工作。

当需要较大的升压或者降压变换比时，使用变压器可以优化变换器。通过合适的变压器匝比的选择，施加在晶体管和二极管的电压和电流应力可以被最小化，从而具有改进的效率和更低的成本。

通过添加多个次级侧绕组和变换器次级电路，还可以通过廉价的方式获得多个DC输出。改变次级侧匝数比可以获得所需的输出电压。通常只有一个输出电压可以通过控制变换器的占空比来调节，因此对于辅助输出电压需要具有更大的容差。在假定主输出电压得到理想调节控制后，交叉调节(cross regulation)是对辅助输出电压的一种度量。

具有匝数比为\(n_{1}:n_{2}:n_{3}:...\)的物理多绕组变压器如图6.16(a)所示。一个简单的等效电路如图6.16(b)所示，这足以理解大多数变压器隔离变换器电路的工作情况。这个模型假设了绕组之间具有完美的耦合，忽略了损耗。下一章将讨论更加准确的模型。理想变压器遵循下面规则：

\[\frac{v_{1}(t)}{n_{1}}= \frac{v_{2}(t)}{n_{2}}= \frac{v_{3}(t)}{n_{3}} \ ... \\ 0=n_{1}{i_{1}}^{'}(t)+n_{2}{i_{2}}(t)+n_{3}{i_{3}}(t)+... \tag{6.16} \]

与理想变压器并联的是一个被称为励磁电感的电感\(L_{M}\)，在图中被称为变压器初级(primary)。

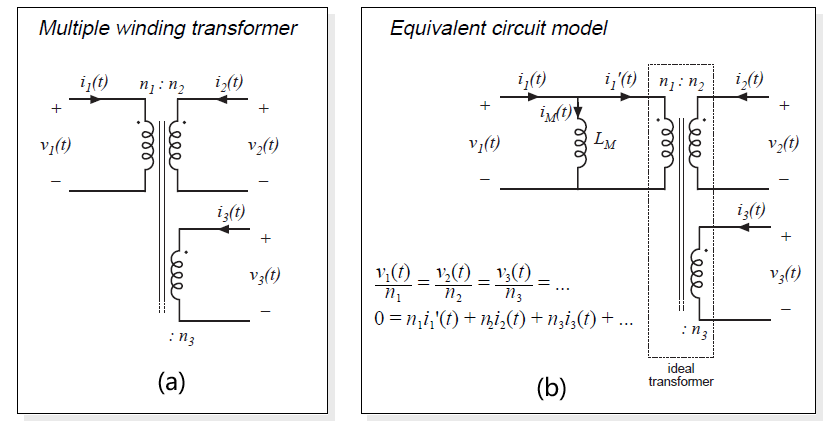
Fig 6.16 Simplified model of a multiple-winding transformer：(a) schematic symbol, (b) equivalent circuit containing a magnetizing inductance and ideal transformer.

物理实现的变压器必须有一个励磁电感。比如，假设我们断开除初级绕组以外的所有绕组，然后，磁芯上就只有一个绕组，就变为了一个电感。实际上，图6.16(b)的等效电路也预测了这种特性。

磁化电流\(i_{M}(t)\)与变压器铁芯内部的磁场\(H(t)\)成正比。变压器铁芯材料的\(B-H\)特性(图6.17)决定了励磁电流的特性。例如，当磁化电流\(i_{M}(t)\)太大时，磁场强度\(H(t)\)幅值使得铁芯饱和。然后，励磁电感的值变得非常小，有效地使变压器短路。

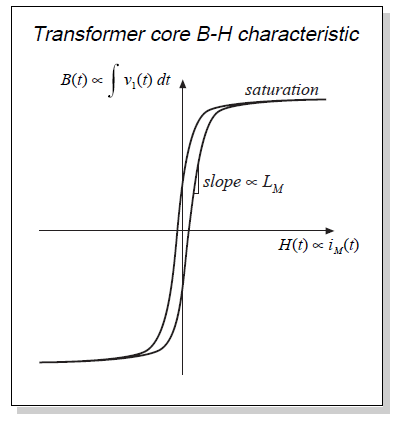
Fig 6.17 \(B-H\) characteristics of transformer core

励磁电感的存在解释了为什么变压器不能在直流电路中工作：在直流的情况下，励磁电感的阻抗为0，使得绕组短路。在一个设计良好的变压器中，在预期工作频率范围内，励磁电感的阻抗很大，此时励磁电流的幅值要小于\(i_{1}(t)\)，就会存在\({i_{1}}^{'}(t) \approx i_{1}(t)\)，变压器表现为近似的理想变压器特性。应该强调的是，励磁电流\(i_{M}(t)\)和初级绕组电流\(i_{1}(t)\)是相互独立的量。

励磁电感遵循电感的所有原理规则。在图6.16(b)的模型中，初级绕组电压\(v_{1}(t)\)直接施加在励磁电感\(L_{M}\)上，因此：

\[v_{1}(t)=L_{M} \frac{d i_{M}(t)}{dt} \tag{6.17} \]

整理得到：

\[i_{M}(t)-i_{M}(0)= \frac{1}{L_{M}} \int _{0} ^{t} v_{1}(\tau)d \tau \tag{6.18} \]

因此，励磁电流取决于施加于绕组电压的积分。电感伏秒平衡这里也适用：当变换器工作于稳态时，施加于励磁电感上电压的直流分量必须为0：

\[0=\frac{1}{T_{s}} \int _{0} ^{T_{s}} v_{1}(t)dt \tag{6.19} \]

由于励磁电流正比于施加于绕组电压的积分，因此重要的是改电压的直流分量为0。否则，在每个开关周期内，励磁电流都有净增加，最终就会导致过大的电流使变压器饱和。

可以通过在含变压器电路中插入图6.16(b)所示模型替代变压器来理解变换器工作原理。然后，如前几章所述进行分析，将磁化电感视作其他变换器中的电感进行分析。

实际的变压器一定会包括漏感。连接绕组的磁通中一小部分可能没有连接其他绕组。在双绕组变压器中，漏感可以用于绕组串联的小电感来模拟。在大多数隔离型变换器中，漏感是一种不理想情况，会导致开关损耗，晶体管峰值电压升高，降低交叉调整等，但对基本变换器的原理没有影响。

有多种将变压器隔离集成到DC-DC变换器中的方法。全桥，半桥，正激和推挽是buck变换器常见的隔离型版本。类似的boost变换器的隔离也是已知的。反激变换器是buck-boost的隔离版本。这些隔离变换器以及隔离的Cuk和SEPIC变换器将在本节中讨论。

6.3.1 全桥和半桥隔离Buck变换器

全桥变压器隔离的buck变换器如图6.18(a)所示。其展示了一个包含中心抽头次级绕组的版本，该电路通常用于产生低输出电压的变换器中。中间抽头的次级绕组的两半可以看做独立的绕组，因此我们可以将其视为匝比为\(1:n:n\)的三绕组变压器。将变压器替换为图6.16(b)所示的等效电路模型后，即可获得图6.18(b)的电路。典型波形如图6.19所示。将图6.19的\(v_{s}(t)\)和\(i(t)\)与图2.1(b)和2.10相比，变换器输出部分与非隔离buck变换器相似。

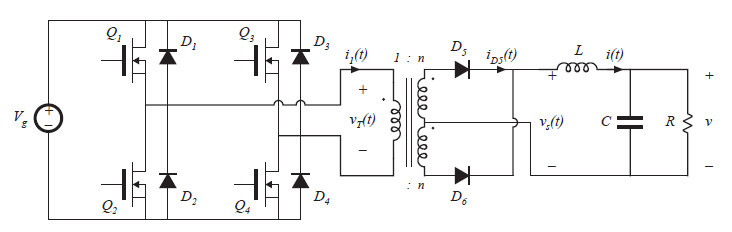
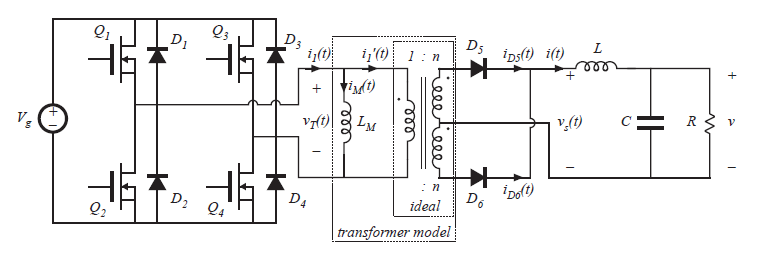
Fig 6.18 Full-bridge transformer-isolated buck converter:(a) schematic diagram, (b) replacement of transformer with equivalent circuit model.

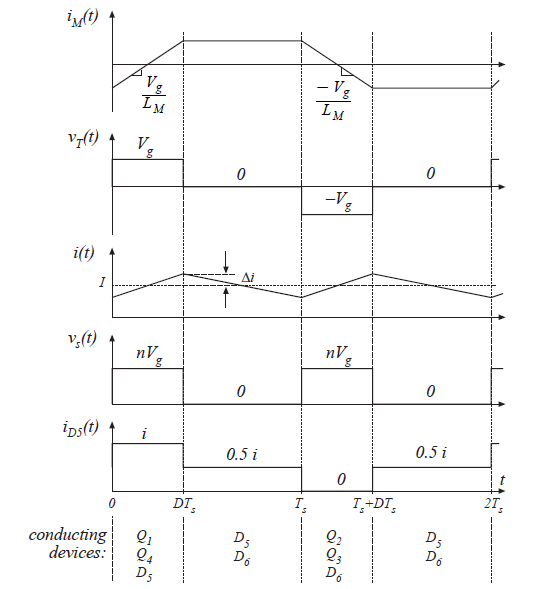
Fig 6.19 Waveforms of the full-bridge transformer-isolated buck converter.

在第一个子区间\(0<t<DT_{s}\)内，晶体管\(Q_{1}\)和\(Q_{4}\)导通，变压器初级侧电压为\(v_{T}=V_{g}\)。这个正电压使得励磁电流\(i_{M}(t)\)以斜率\(V_{g}/L_{M}\)增大。中间抽头次级绕组两端出现的电压为\(nV_{g}\)，极性标记为正。二极管\(D_{5}\)正向偏置，二极管\(D_{6}\)反向偏置。电压\(v_{s}(t)\)等于\(nV_{g}\)，并且输出滤波电感的电流\(i(t)\)流过二极管\(D_{5}\)。

第二个子区间\(DT_{s}<t<T_{s}\)内，可以有几种晶体管的控制方式。在最常见的方案中，所有的四个晶体管都关闭，因此变压器的电压为\(v_{T}=0\)。可替代的，\(Q_{2}\)和\(Q_{4}\)可以导通，或者\(Q_{1}\)和\(Q_{3}\)可以导通。在任何情况下，在这个子区间内，二极管\(D_{5}\)和\(D_{6}\)都是正偏的。每个二极管导通的电流都近似为输出滤波电感电流的一半。

实际上，二极管电流\(i_{D5}\)和\(i_{D6}\)在第二个子区间内都是输出电感电流和变压器励磁电流的函数。在理想情况下（无励磁电流）这个变压器会使得\(i_{D5}(t)\)和\(i_{D6}(t)\)在幅值上相等，这是由于，如果\({i_{1}}^{'}(t)=0\)，那么\(ni_{D5}(t)=ni_{D6}(t)\)。但两个二极管的电流之和又等于输出电感的电流：

\[i_{D5}(t)+i_{D6}(t)=i(t) \tag{6.20} \]

因此，在第二个子区间内，必有\(i_{D5}=i_{D6}=0.5i\)。而实际中，二极管电流会与这个结果略有不同，就是由于励磁电流不为0。

图6.18(b)的理想变压器电流遵循：

\[{i_{1}}^{'}(t)-ni_{D5}(t)+ni_{D6}(t)=0 \tag{6.21} \]

理想变压器初级侧节点方程为：

\[i_{1}(t)=i_{M}(t)+{i_{1}}^{'}(t) \tag{6.22} \]

结合上述两式消除\({i_{1}}^{'}(t)\)，得到：

\[i_{1}(t)-ni_{D5}(t)+ni_{D6}(t)=i_{M}(t) \tag{6.23} \]

一般情况下，公式6.23和6.20描述了变压器绕组在第二个子区间内的电流。根据式6.23，磁化电流\(i_{M}(t)\)将会流过初级绕组，次级绕组中的一个，或者在三个绕组中进行分配。如何分配就取决于导通晶体管和二极管的\(i-v\)特性曲线以及变压器的漏感。当\(i_{1}=0\)时，式6.20和 6.23的解为：

\[i_{D5}(t)=\frac{1}{2}i(t)-\frac{1}{2n}i_{M}(t) \\ i_{D6}(t)=\frac{1}{2}i(t)+\frac{1}{2n}i_{M}(t) \tag{6.24} \]

如果当\(i_{M}<<ni\)，则\(i_{D5}\)和\(i_{D6}\)分别近似等于\(0.5i\)。

下一个开关周期\(T_{s}<t<2T_{s}\)以类似的方式进行工作，只是激励变压器的电压变为了反方向。在\(T_{s}<t<(T_{s}+DT_{s})\)期间，晶体管\(Q_{2}\)和\(Q_{3}\)二极管\(D_{6}\)导通。施加在变压器初级侧绕组的电压为\(v_{T}=-V_{g}\)，其使得励磁电流以斜率\(-V_{g}/L_{M}\)下降。电压\(v_{s}(t)\)等于\(nV_{g}\)，输出电感电流\(i(t)\)流过二极管\(D_{6}\)。类似于前述分析过的第二个子区间，在\((T_{s}+DT_{s})<t<2T_{s}\)期间，二极管\(D_{5}\)和\(D_{6}\)都导通。可以看到输出滤波元件的纹波频率为\(f_{s}=1/T_{s}\)。然而，变压器波形频率为\(0.5f_{s}\)。

对励磁电感应用电感的伏秒平衡原理，当变换器在稳态下运行时，变压器的电压\(v_{T}(t)\)d的平均值必须为0。在第一个开关周期内，正的伏秒被施加于变压器，大约等于：

\[|V_{g}-(Q_{1}\ and\ Q_{4}\ foward\ voltage\ drops)|(Q_{1}\ and\ Q_{4}\ conduction\ time) \tag{6.25} \]

在第二个开关周期，负的伏秒施加于变压器，给出：

\[-|V_{g}-(Q_{2}\ and\ Q_{3}\ foward\ voltage\ drops)|(Q_{2}\ and\ Q_{3}\ conduction\ time) \tag{6.26} \]

净伏秒，也就是式6.25和6.26的和，应该等于0。尽管全桥的方案使得这种情况近似是成立的，但实际上是存在不平衡现象的，比如晶体管正向压降和开关时间的微小不同，因此\(<v_{T}>\)很小，但不等于0。所以，在每两个开关周期，励磁电流的大小会净增加，这种增加可能会导致晶体管的正向压降减小从而补偿不平衡。但是如果不平衡情况过大，那么励磁电流会变得足够大以至于使得变压器饱和。

通过在变压器初级串联电容可以避免稳态情况下的变压器饱和。然后，不平衡会在电容两端感应出一个直流电压分量而不是变压器的初级绕组，从而避免饱和。另一种解决方法是使用电流控制编程(current-programmed control)，这将在下一章中进行讨论。使用电流控制编程时，可以省略串联的电容。

通过对输出滤波电感应用伏秒平衡，直流负载电压一定等于\(v_{s}(t)\)的直流分量:

\[V=<v_{s}> \tag{6.27} \]

通过观察图6.19中的\(v_{s}(t)\)波形，有\(<v_{s}>=nDV_{g}\)。因此：

\[V=nDV_{g} \tag{6.28} \]

因此，就像在buck变换器中一样，我们可以通过晶体管的占空比\(D\)的变化来改变输出电压。同时还可以通过变压器的匝数比的调整来获得额外的增加或减小。公式6.28对于连续导通模式运行的变换器有效；与非隔离buck变换器相同，全桥和半桥变换器可以在轻载下以不连续导通模式运行。变换器可以在整个连续的占空比\(0\leq D<1\)范围内运行。

晶体管\(Q_{1}\)和\(Q_{2}\)一定不能同时导通，否则将会使直流源\(V_{g}\)短路，引起直通短路尖峰。这种晶体管的交叉导通条件可能导致效率低下和晶体管故障。可以通过在晶体管关断和导通之间引入死区延迟来防止这种交叉导通。二极管\(D_{1}\)到\(D_{4}\)保证晶体管的峰值电压被限制为直流输入电压，并且为轻载条件下的变压器励磁电流提供通路。全桥电路的开关变换细节将在后面的章节中结合零电压开关现象进一步讨论。

全桥变换器通常用于功率大于750W的开关电源。由于其元件数较多-需要四个晶体管及其驱动电路，因此通常不以较低的功率运行。变压器利用率较高，因此其体积较小。特别的，由于变压器励磁电流可以为正也可以为负，变压器磁芯利用率也较好。磁芯的整个\(B-H\)曲线都能用得到。然后实际中磁通摆幅通常受限于铁损。变压器初级绕组得到了充分利用，但带有中间抽头的二次绕组并没有：次级绕组仅在交替的开关周期内传输功率。同样，在子区间2内，次级绕组电流会产生损耗，但并不传输功率至负载。全桥变换器的详细介绍将在下一章中讨论。

图6.20为buck型变压器隔离半桥变换器，其典型波形如图6.21。这个电路与图6.18(a)所示的全桥变换器相似，只是将其中的晶体管\(Q_{3}\)和\(Q_{4}\)及其反并联二极管换成了大电容\(C_{a}\)和\(C_{b}\)。通过对变压器励磁电感应用伏秒平衡，电容\(C_{b}\)上的直流电压等于晶体管\(Q_{2}\)上的直流电压分量，或者说就是\(0.5V_{g}\)。变压器初级侧电压在\(Q_{1}\)导通时是\(0.5V_{g}\)，当\(Q_{2}\)导通时是\(-0.5V_{g}\)。\(v_{T}(t)\)的幅值是全桥的一半，并且输出电压也就是相当于结果乘一个0.5：

\[V=0.5nDV_{g} \tag{6.29} \]

可以通过将变压器匝比\(n\)加倍来补偿这个系数0.5，但是，这样又会导致晶体管的电流加倍。

所以，半桥电路仅需要两个晶体管而不是四个，但是这两个晶体管必须处理的电流是全桥的二倍。所以，半桥电路通常应用于较低的功率水平，而这种大电流晶体管比较容易获得，并且其中的低开关元件数很重要。变压器铁芯和绕组和全桥电路中的应用相同，晶体管的峰值电压被二极管\(D_{1}\)和\(D_{2}\)钳位到\(V_{g}\)。并且可以根据需要省略电容\(C_{a}\)。电流编程模式（current-programmed mode）通常不适用于半桥变换器。

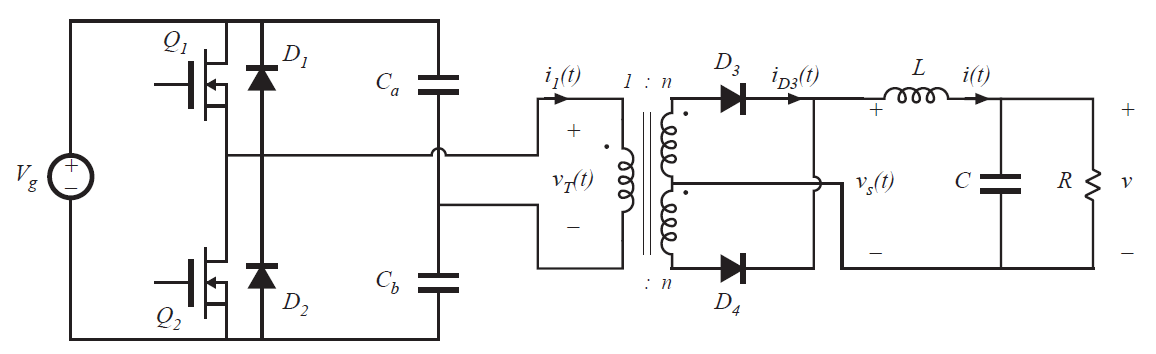
Fig 6.20 Half-bridge transformer-isolated buck converter

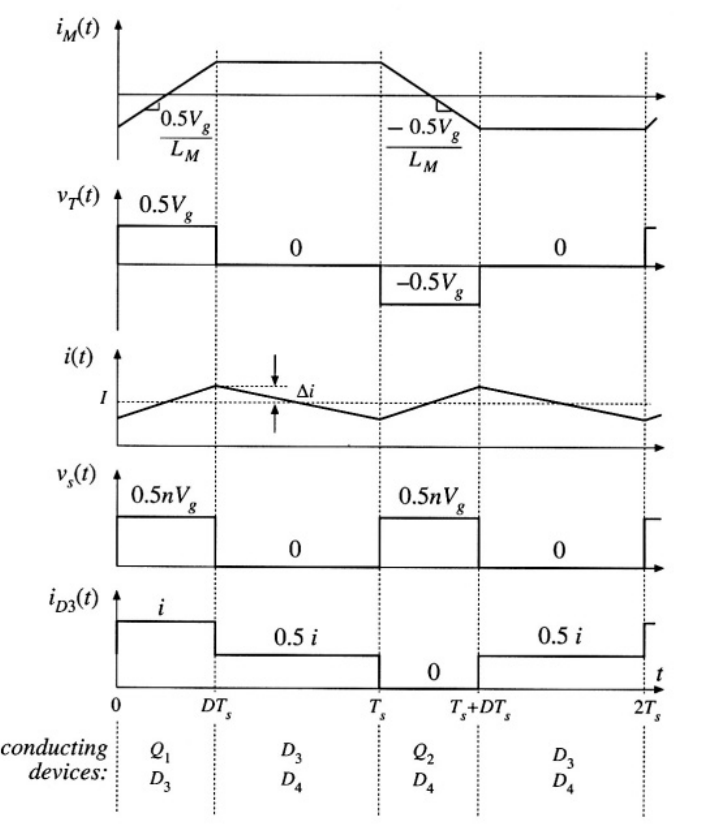
Fig 6.21 Waveforms of the half-bridge transformer-isolated buck converter.

6.3.2 正激变换器

正激变换器如图6.22所示，该变压器隔离的变换器基于buck变换器演化而来。它只需要一个晶体管，因此可以在低于半桥和全桥应用的功率场景下使用。与其他buck型变换器相同的其具有无脉动输出电流使其适合于高输出电流的应用场合。最大占空比受到数值限制；对于常规选择\(n_{1}=n_{2}\)时，占空比应限制在\(0 \leq D<0.5\)。

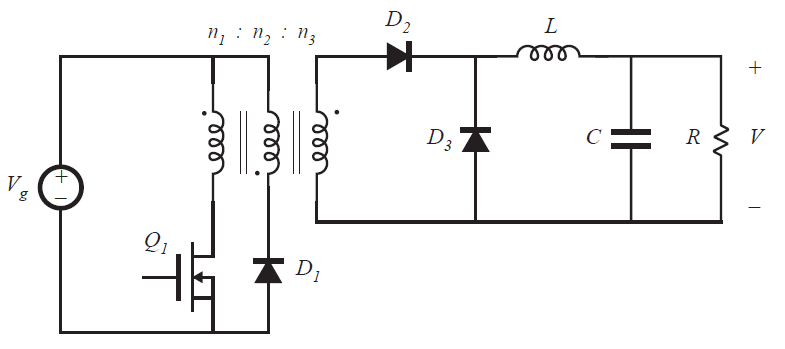
Fig 6.22 Single-transistor forward converter

当晶体管关断时，变压器励磁电流复位到0。通过用图6.16(b)的变压器等效电路代替图6.22中的三绕组变压器就可以理解这个原理。替代后电路如图6.23所示，典型波形如图6.24所示。励磁电感\(L_{M}\)与二极管\(D_{1}\)一起必须在不连续导通模式下运行。输出电感\(L\)与二极管\(D_{3}\)一起可在连续或者不连续导通模式下运行。图6.24的波形是电感\(L\)连续工作模式的示意图。在每个开关周期内，会出现三个子区间，如图6.25所示。

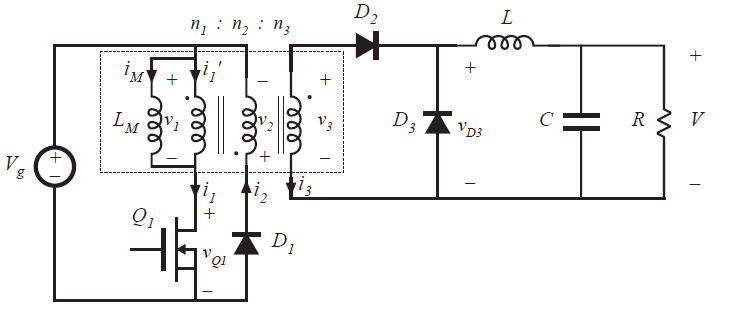
Fig 6.23 Forward converter, with transformer equivalent circuit model

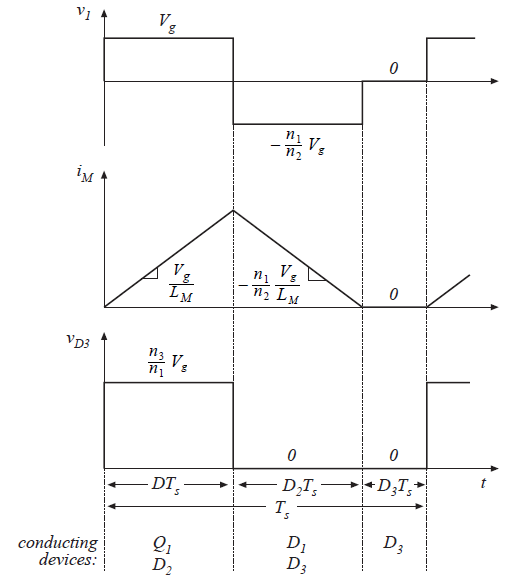
Fig 6.24 Waveforms of the forward converter.

在第一个子区间内，晶体管\(Q_{1}\)导通，获得如图6.25(a)所示的电路。二极管\(D_{2}\)开始正向偏置，二极管\(D_{1}\)和\(D_{3}\)反向偏置。电压\(V_{g}\)施加于变压器的初级绕组，并且因此变压器励磁电流\(i_{M}(t)\)如图6.24所示以斜率\(V_{g}/L_{M}\)上升。二极管\(D_{3}\)的电压等于\(V_{g}\)乘以匝比\(n_{3}/n_{1}\)。

当晶体管\(Q_{1}\)关断时，第二个子区间开始。即获得了图6.25(b)所示的电路。变压器励磁电流\(i_{M}(t)\)在此时是正的，并且电流必须持续流动。由于晶体管\(Q_{1}\)关断，根据等效电路模型，励磁电流必须流过理想变压器的初级侧。可以看到安匝数\(n_{1}i_{M}\)从初级绕组的同名端流出。因此根据式6.16，相同的总安匝数一定会从其他绕组的同名端流入。二极管\(D_{2}\)阻止了电流流入绕组3的同名端。因此，这时电流\(i_{M}n_{1}/n_{2}\)必须流入绕组2的同名端。所以，二极管\(D_{1}\)正偏，二极管\(D_{2}\)反偏。电压\(v_{g}\)直接施加于绕组2，因此，相比于绕组1，励磁电感的电压为\(-V_{g}n_{1}/n_{2}\)。这个负电压使得励磁电感以斜率\(-V_{g}n_{1}/(n_{2}L_{M})\)下降。由于二极管\(D_{2}\)反偏，二极管\(D_{3}\)必须开通来导通输出电感电流\(i(t)\)。

当励磁电流降为0时，二极管\(D_{1}\)开始反偏。此时进入第三个子区间，并且获得了图6.25(c)所示的电路。\(Q_{1}\)，\(D_{1}\)和\(D_{2}\)都工作在关断状态，并且由于开关周期的平衡，励磁电流保持为0。

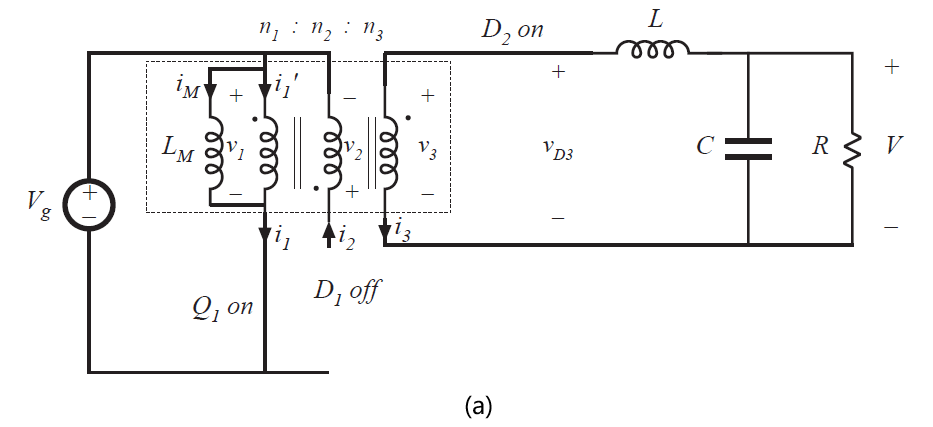
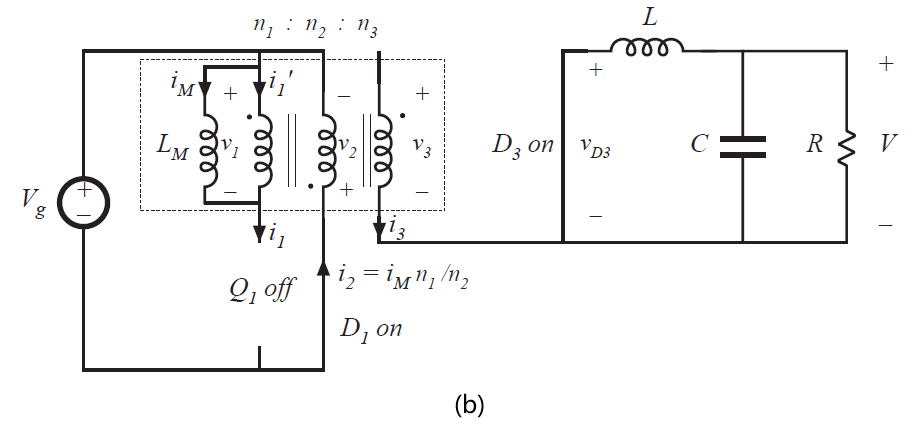
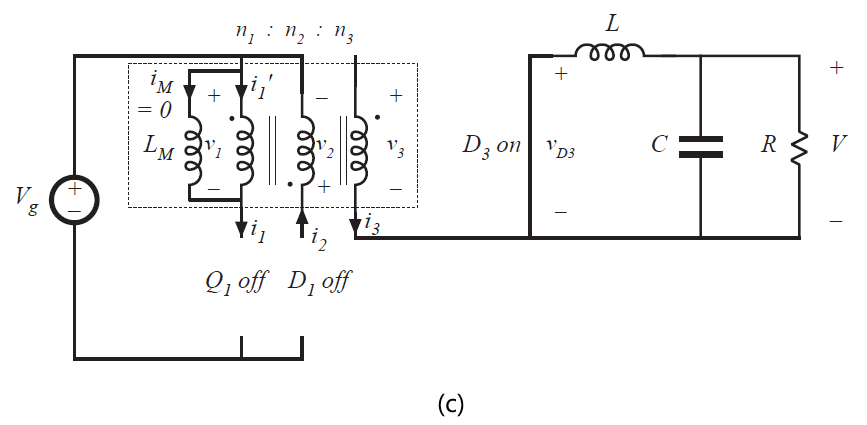
Fig 6.25 Forward converter circuit: (a) during subinterval 1, (b) during subinterval 2, (c)during subinterval 3.

通过对变压器励磁电感应用伏秒平衡，初级绕组的电压\(v_{1}(t)\)平均值必须为0。参考图6.24，电压\(v_{1}(t)\)的平均值为：

\[<v_{1}>=D(V_{g})+D_{2}(-V_{g}n_{1}/n_{2})+D_{3}(0)=0 \tag{6.30} \]

占空比\(D_{2}\)为:

\[D_{2}=\frac{n_{2}}{n_{1}}D \tag{6.31} \]

注意到\(D_{3}\)不可能为负，且有\(D+D_{2}+D_{3}=1\)，则：

\[D_{3}=1-D-D_{2} \geq 0 \tag{6.32} \]

将式6.31代入6.32得到：

\[D_{3}=1-D(1+\frac{n_{2}}{n_{1}}) \geq 0 \tag{6.33} \]

那么求出\(D\)为：

\[D \leq \frac{1}{1+\cfrac{n_{2}}{n_{1}}} \tag{6.34} \]

那么最大占空比就受限了。对于通常选择\(n_{1}=n_{2}\)，这个限制变为：

\[D \leq \frac{1}{2} \tag{6.35} \]

如果违背了这个限制条件，那么晶体管的截止时间不足以在开关周期结束之前将变压器的励磁电流复位至0，变压器就可能会发生饱和。

当\(n_{1}=n_{2}\)时，变压器励磁电流\(i_{M}(t)\)波形如图6.26所示。图6.26(a)描绘了当\(D<0.5\)的工作情况。励磁电感与二极管一起工作在不连续导通模式，并且\(i_{M}(t)\)在每个开关周期结束之前会复位到0。图6.26(b)描绘了晶体管占空比\(D>0.5\)的情况，其中没有第三个子区间，并且励磁电感工作在连续导通模式。此外，子区间2不足以磁化电流复位到0。因此，在每个开关周期中磁化电流\(i_{M}(t)\)会有净增量。最终磁化电流增大到一定程度似的变压器饱和。

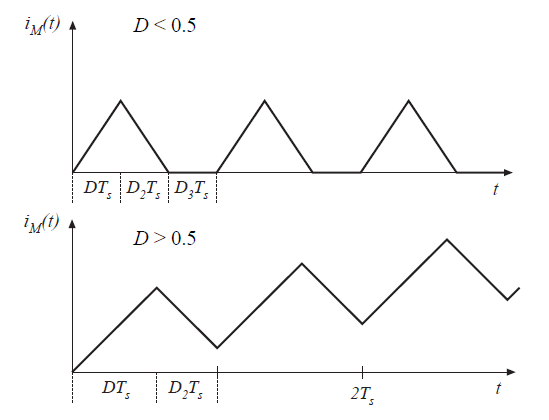
Fig 6.26 Magnetizing current waveforms，forward converter: (a) DCM, D<0.5; (b) CCM, D>0.5

对电感\(L\)应用电感伏秒平衡即可得到变换器的输出电压。电感\(L\)的电压直流分量必须为0，因此输出电压的直流分量就应该等于二极管\(D_{3}\)电压\(v_{D3}(t)\)的直流分量。\(v_{D3}(t)\)的波形如图6.24所示，其平均值为：

\[<v_{D3}>=V=\frac{n_{3}}{n_{1}}DV_{g} \tag{6.36} \]

这就是连续导通模式下（输出电感）正激变换器的输出电压解。其同时还要受到式6.34的约束。

从式6.34我们可以看到，可以通过减小匝比\(n_{2}/n_{1}\)来增大最大占空比\(D\)。这将会使励磁电流\(i_{M}(t)\)在第二个子区间内减小的更快，变压器复位的最快。不幸的是，这同时会增加晶体管\(Q_{1}\)的电压应力。晶体管\(Q_{1}\)承受的最大电压是在子区间2内，对图6.25(b)求解这个电压为:

\[max(v_{Q1})=V_{g}(1+\frac{n_{1}}{n_{2}}) \tag{6.37} \]

对于通常情况\(n_{1}=n_{2}\)，晶体管在子区间2内的电压为\(2V_{g}\)。在实际中，由于还有与变压器漏感相关的振铃，还能观察到更高的电压。因此，降低匝比可以增加最大晶体管占空比，但这是以增加晶体管阻断电压为代价的。双管正激变换器如图6.27所示。晶体管\(Q_{1}\)和\(Q_{2}\)以相同的门极信号驱动，所以他们在子区间1内都可以导通，并且在子区间2和3内都关断。变换器次级侧与单管正激变换器相同；二极管\(D_{3}\)在子区间1内导通，二极管\(D_{4}\)在子区间2和3内导通。在子区间2内，励磁电流\(i_{M}(t)\)使得二极管\(D_{1}\)和\(D_{2}\)正向偏置。变压器初级绕组反向连接到\(V_{g}\)，极性与子区间1相反。励磁电流然后以斜率\(-V_{g}/L_{M}\)减小。当励磁电流减小到0，二极管\(D_{1}\)和\(D_{2}\)变为反向偏置。然后为了整个开关周期的平衡，励磁电流保持为0。所以，当\(n_{1}=n_{2}\)时，双管正激电路与单管相似。占空比也是限制为\(D<0.5\)。这个变换器的优点就是，晶体管的最大阻断电压被限制到\(V_{g}\)，并且被二极管\(D_{2}\)和\(D_{3}\)钳位。双管正激电路典型应用功率等级与半桥电路的应用场合相似。

正激变换器的变压器利用率非常好。由于变压器的励磁电流不能为负的，因此只能使用铁芯\(B-H\)曲线的一半。这似乎让我们觉得，正激变换器的变压器会是全桥或者半桥变换器的二倍大。然而，在现代高频变换器中，磁通摆幅的限制主要是磁芯损耗而不是磁芯材料的饱和磁通。因此，正激变换器的变压器磁芯利用可以和全桥或者半桥一样好。由于正激变换器不需要中心抽头绕组，变压器的初级和次级绕组的使用比全桥，半桥或者推挽式电路的利用更好。在子区间1内，所有的可用绕组铜都用于向负载传输功率。在子区间2和3内，基本没有不必要的电流流动。通常，励磁电流与反射负载电流相比较小，并且对变压器的利用率影响可忽略不计。所以，变压器铁芯和绕组在现代的正激变换器中得到了有效利用。

6.3.3 推挽隔离Buck变换器

如图6.28所示为推挽(push-pull)隔离buck变换器。其次级侧与全桥和半桥电路相同，并且具有相同的波形。初级侧包含一个中心抽头变压器。晶体管\(Q_{1}\)在第一个开关周期内导通时间为\(DT_{s}\)。晶体管\(Q_{2}\)在下一个开关周期内导通相同的时间以保证维持初级侧绕组的伏秒平衡。变换器波形如图6.29所示。这个变换器可以在整个占空比\(0 \leq D<1\)范围内工作，其电压变换比为：

\[V=nDV_{g} \tag{6.38} \]

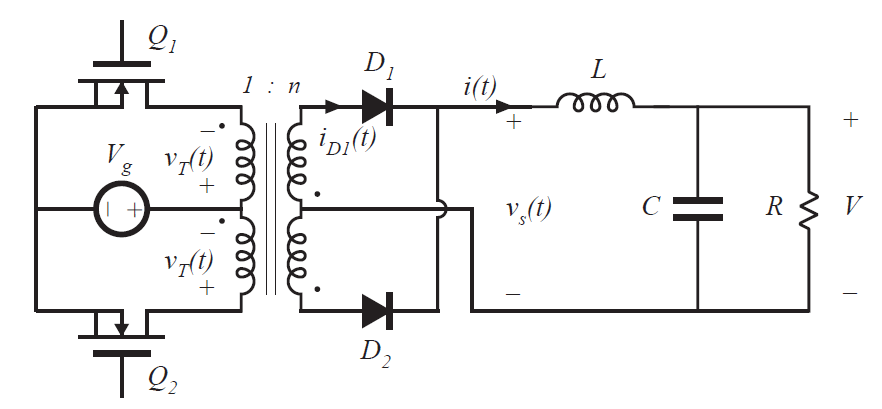
Fig 6.28 Push-pull isolated buck converter

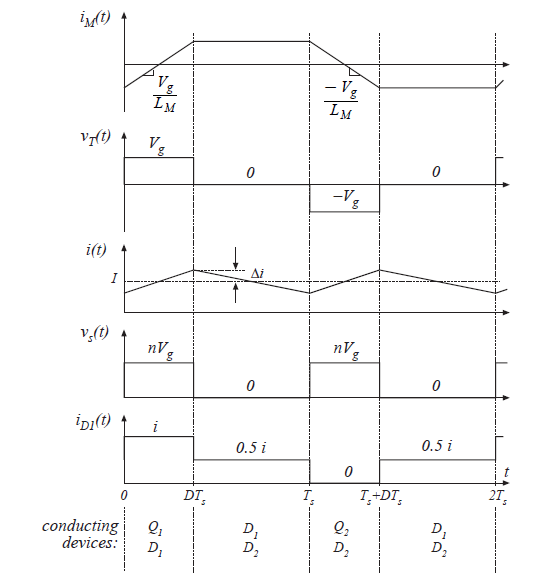
Fig 6.29 Waveforms of the push-pull isolated buck converter.

该变换器常在低输入电压下使用。其通常表现出较低的初级侧传导损耗，这是因为在任何时刻，只有一个晶体管与电源\(V_{g}\)串联连接。在晶体管占空比接近于1的情况下工作的能力还可以使得匝比\(n\)最小，从而减小晶体管的电流。推挽式电路容易出现变压器饱和问题。由于不能保证晶体管\(Q_{1}\)和\(Q_{2}\)的正向压降和导通时间完全一致，因此非常小的不平衡都是导致变压器初级侧的电压直流分量不为0。那么，在每两个开关周期内，励磁电流的净值会增加，如果这种不平衡持续存在，那么励磁电流最终会变得足够大导致变压器饱和。可以采用电流程控来减轻变压器饱和问题。不建议使用占空比控制来控制推挽变换器。

变压器的铁芯材料和次级绕组的利用率类似全桥变换器。磁通和励磁电流可以为正也可以为负，所以，如果需要的话，可以使用整个\(B-H\)环路。由于初级绕组和次级绕组都是中心抽头的，因此其利用率不是最佳的。

6.3.4 反激变换器

Fig 6.30 Derivation of the flyback converter: (a) a buck-boost converter; (b) inductor L is wound with two parallel wires; (c) inductor windings are isolated, leading to the flyback converter; (d) with a \(1:n\) turns ratio and positive output.

反激变换器是基于buck-boost的变换器。如图6.30是其电路拓扑推演过程。图6.30(a)是一个基本buck-boost变换器，其开关由MOSFET和二极管实现。图6.30(b)中，电感绕组被分为匝比为\(1:1\)的两个绕组。电感的基本功能没变，并联的绕组等效由较大导线构成的单个绕组。在图6.30(c)中，两个绕组之间的连接被打破，其中一个绕组在晶体管\(Q_{1}\)导通时工作，另一个绕组在\(D_{1}\)导通时工作。由图6.30(b)来看，两个绕组中的总电流并没有发生变化；然而电流在两个绕组中的分配发生了变化。在两种情况下，电感内部的磁场是相同的。尽管使用与变压器相同的符号来表示双绕组磁性器件，但更具细节描述性的名称是“双绕组电感”。有时也被称为反激变压器。与理想变压器不同，电流不会同时在反激变压器的两个绕组中流动。图6.30(d)给出了反激变换器的常规电路。MOSFET的源极接到初级侧的地（ground），简化了栅极驱动电路的设计。变压器同名端反向连接，可以获得正的输出电压。引入\(1:n\)的匝数比可以更好的实现变换器的优化。

可以通过插入图6.16(b)的等效模型来替代反激变压器分析反激变换器的工作。然后就获得了图6.31(a)。励磁电感\(L_{M}\)的功能与图6.30(a)的原始buck-boost变换器的电感\(L\)相同。当晶体管\(Q_{1}\)导通时，能量由直流源\(V_{g}\)存储至电感\(L_{M}\)。当二极管\(D_{1}\)导通时，存储的能量转移至负载，并且电感电压与电流根据匝数比\(1:n\)进行缩放。

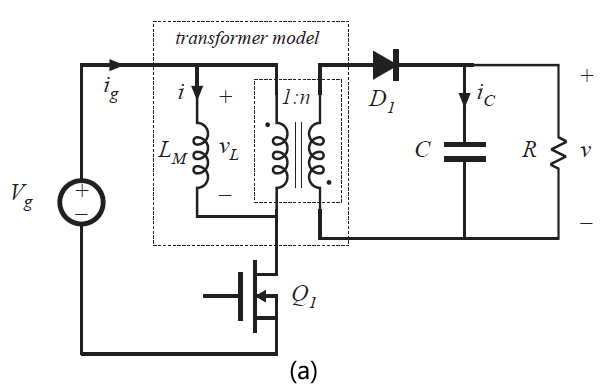
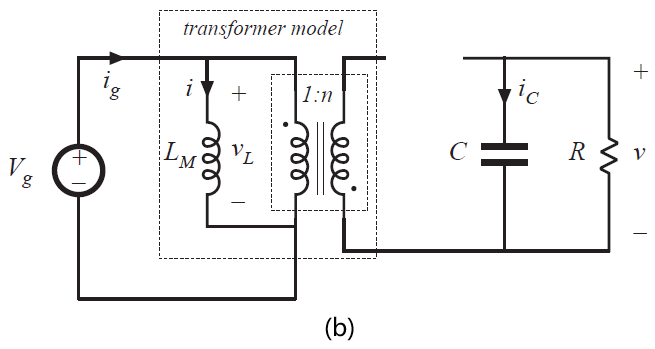
Fig 6.31 Flyback converter circuit：(a) with transformer equivalent circuit model, (b) during subinterval 1, (c) during subinterval 2

在第一个子区间内，晶体管\(Q_{1}\)导通，变换器电路模型退化为6.31(b)所示。电感电压\(v_{L}\)，电容电流\(i_{C}\)以及直流源电流\(i_{g}\)为：

\[v_{L}=V_{g} \\ i_{C}=- \frac{v}{R} \\ i_{g}=i \tag{6.39} \]

假设变换器工作于连续导通模式，具有较小的电感电流纹波和电容电压纹波，励磁电流\(i\)和电容电压\(v\)分别近似为他们的直流分量\(I\)和\(V\)。式6.39变为：

\[v_{L}=V_{g} \\ i_{C}=-\frac{V}{R} \\ i_{g}=I \tag{6.40} \]

在第二个子区间内，晶体管处于关断状态，二极管导通。如图6.31(c)所示的等效电路可以获得。在这个子区间内，初级侧励磁电感的电压\(v_{L}\)，电容电流\(i_{C}\)和直流电源电流\(i_{g}\)为：

\[v_{L}=-\frac{v}{n} \\ i_{C}=\frac{i}{n}- \frac{v}{R} \\ i_{g}=0 \tag{6.41} \]

对于所有的子区间，在变压器的同一侧上一致地定义\(v_{L}(t)\)是非常重要的。在进行小纹波近似时，可以获得：

\[v_{L}=\frac{V}{n} \\ i_{C}=\frac{I}{n}- \frac{V}{R} \\ i_{g}=0 \tag{6.42} \]

\(v_{L}(t)\)，\(i_{C}(t)\)和\(i_{g}(t)\)在连续导通模式下的波形如图6.32所示。

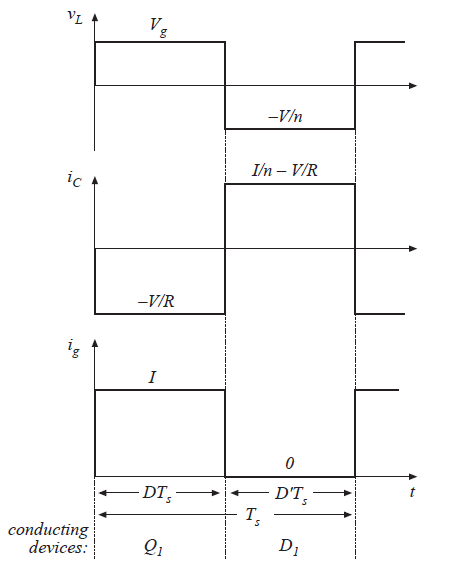
Fig 6.32 Flyback converter waveforms, continuous conduction mode.

对初级侧励磁电感应用伏秒平衡可以得到：

\[<v_{L}>=D(V_{g})+D^{'}(-\frac{V}{n})=0 \tag{6.43} \]

求解变换比为：

\[M(D)=\frac{V}{V_{g}}=n \frac{D}{D^{'}} \tag{6.44} \]

因此反激变换器与buck-boost变换器的变换比是相似的，无非是增加了一个系数\(n\)。

对输出电容利用电荷平衡可以得到：

\[<i_{C}>=D(-\frac{V}{R})+D^{'}(\frac{I}{n}- \frac{V}{R}) \tag{6.45} \]

求解电流\(I\)得到：

\[I=\frac{nV}{D^{'}R} \tag{6.46} \]

这就是初级侧励磁电流的直流分量。电源电流\(i_{g}\)的直流分量为：

\[I_{g}=<i_{g}>=D(I)+D^{'}(0) \tag{6.47} \]

现在就可以构建一个模拟反激变换器直流分量的等效电路。图6.33(a)给出了与电感环路方程6.43和节点方程6.45以及6.47相对应的电路。通过使用理想直流变压器替代受控源，可以获得图6.33(b)所示的电路。这就是反激变换器的直流等效电路。它包含一个\(1:D\)的降压型变换比，然后后面是一个\(D^{'}:1\)的升压型的变换比，并且有一个由于反激变压器带来的附加因数\(1:n\)。通过使用第三章得到的方法，可以对模型进行精炼(refine)来计算损耗并且预测变换器效率。反激变换器同样可以工作于不连续导通模式，这个分析留在家庭作业中。其结果与第5章得到的buck-boost在DCM下的结果相似，但结果中包含一个\(1:n\)系数的影响。

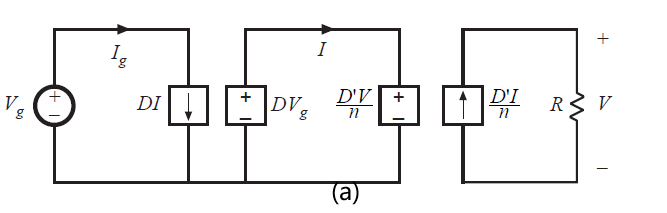
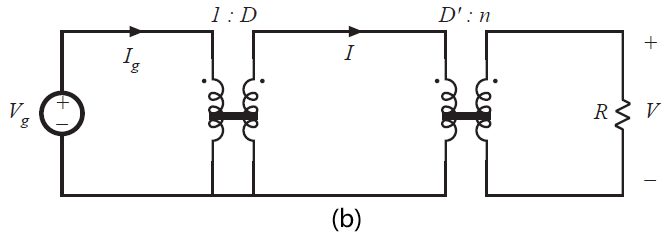
Fig 6.33 Flyback converter equivalent circuit model, CCM: (a) circuits corresponding to Eqs. 6.43 6.45 and 6.47, (b) equivalent circuit containing ideal dc transformers.

反激变换器通常用于50至100W功率范围，以及电视和计算机显示器的高压电源。它具有零件数非常少的优势。使用最少的零件数就可以获得多个输出：每个额外的输出仅需要一个额外的绕组，二极管和电容，但是与全桥，半桥或者双管正激变换器相比，反激变换器具有晶体管电压应力搞和交叉调节(cross regulation)差的缺点。晶体管的峰值电压等于直流输入电压\(V_{g}\)加上负载反射电压\(V/n\)；而实际上，由于存在与变压器漏感相关的振铃现象，会有额外的附加电压应力。由于元件执行的功能不同，很难对反激变压器和基于buck的一些电路的变压器进行充分的比较。反激变压器的励磁电流是单极性的，因此不能使用超过\(B-H\)曲线的一般。励磁电流也必定包含很大的直流分量。然而，在旨在以不连续导通模式工作的设计中，反激变压器的尺寸可以很小。但是，DCM会导致晶体管，二极管和滤波电容中的峰值电流增加。CCM模式设计需要较大的反激变压器的励磁电感\(L_{M}\)，因此需要较大的反激变压器，但功率级元件的峰值电流较低。

6.3.5 升压型隔离变换器

可以通过将降压型隔离变换器的源与负载取反来得到升压型隔离变换器。已知有很多电路拓扑，这里简要讨论其中的两个。这些变换器在高压电源以及低谐波整流器应用中都有一定的用途。

基于全桥的电路如图6.34所示，其在CCM下的波形如图6.35。第一个和第二个子区间中的电路拓扑与基本非隔离Boost变换器相同，并且当匝比为\(1:1\)时，电感电流\(i(t)\)以及输出电流\(i_{o}(t)\)与非隔离Boost变换器的波形相同。

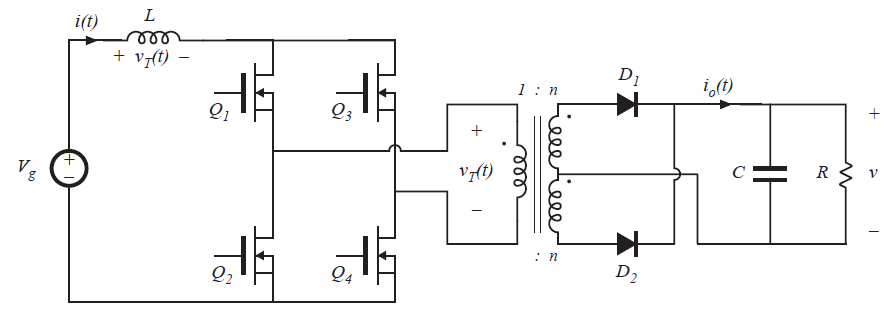
Fig 6.34 Full-bridge transformer-isolated boost converter

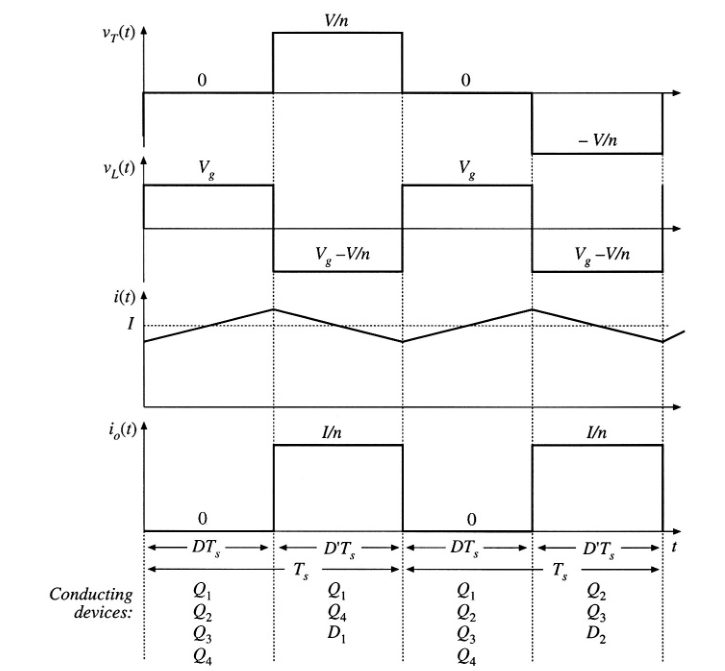
Fig 6.35 Waveforms of the transformer-isolated full-bridge boost converter, CCM.

在第一个子区间内，四个晶体管全部处于导通状态。这使得电感\(L\)直接连接到直流输入电源\(V_{g}\)上，并且导致二极管\(D_{1}\)和\(D_{2}\)均反向偏置。电感电流\(i(t)\)以斜率\(V_{g}/L\)增加，能量从直流源\(V_{g}\)传递到电感\(L\)中。在第二个子区间内，晶体管\(Q_{2}\)和\(Q_{3}\)工作在关断状态，因此电感\(L\)通过晶体管\(Q_{1}\)和\(Q_{4}\)连接，并通过变压器和二极管\(D_{1}\)连接到直流输出。下一个开关周期也是类似的，只是其中第二个子区间内，晶体管\(Q_{1}\)和\(Q_{4}\)处于关断状态，电感\(L\)通过晶体管\(Q_{2}\)和\(Q_{3}\)以及变压器和二极管\(D_{2}\)连接到直流输出。如果晶体管的关断时间和二极管的正向压降相同，则变压器的平均电压为0，并且在两个开关周期内施加到变压器励磁电感的净伏秒数为0。

对电感电压波形\(v_{L}(t)\)应用伏秒平衡可以得到：

\[<v_{L}>=D(V_{g})+D^{'}(V_{g}- \frac{V}{n})=0 \tag{6.48} \]

求解变换比得到：

\[M(D)=\frac{V}{V_{g}}=\frac{n}{D^{'}} \tag{6.49} \]

这个结果类似于Boost变换器的变换比，只是由于变压器的引入增加了系数\(n\)。

晶体管需要阻断负载反射电压为\(V/n=V_{g}/D^{'}\)。实际中，由于变压器漏感引起的振铃现象会导致额外的电压。由于晶体管的瞬时电流受电感的限制，因此由于半导体正向压降或者导通时间这种较小的不平衡引起的变压器饱和不会造成灾难性的影响。实际上一些已知方案在子区间1内有目的性的使变压器处于饱和状态。[13,15]

图6.36(a)所示为推挽变换器。这种电路只需要两个晶体管，每个晶体管需要阻断的电压为\(2V/n\)。其他方面与全桥相似。在子区间1内，两个晶体管均导通；在子区间2内，晶体管之一处于关断状态，能量从电感通过变压器和二极管之一传递到输出。在子区间2的交替切换周期中，晶体管导通，从而保持变压器的伏秒平衡。图6.14的变换器6的Watkins-Johnson变换器就是一种推挽变换器，如图6.36(b)所示。

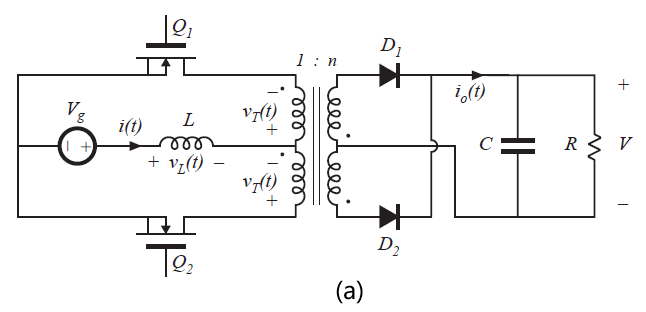
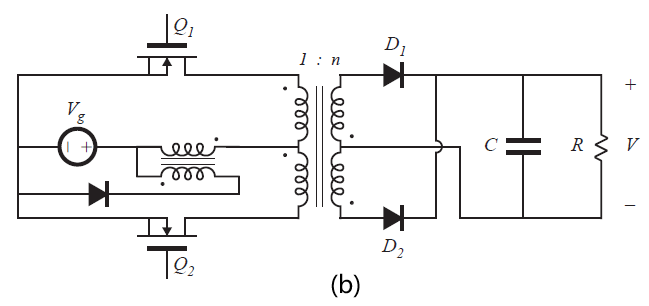
Fig 6.36 Push-pull isolated converters: (a) based on the boost converter, (b) based on the Watkins-Johnson converter.

6.3.6 隔离型SEPIC和Cuk变换器

用于反激式变换器中获得隔离的方法也可以用于SEPIC和SEPIC的反转变换器。根据图6.37(a)，其中的电感\(L_{2}\)可以使用两个绕组来实现，就得到了如图6.37(b)所示的隔离型SEPIC。等效电路如图6.37(c)所示。可以看出，励磁电感完成了原本电感\(L_{2}\)的储能功能。此外，理想变压器还可以提供隔离和匝比。

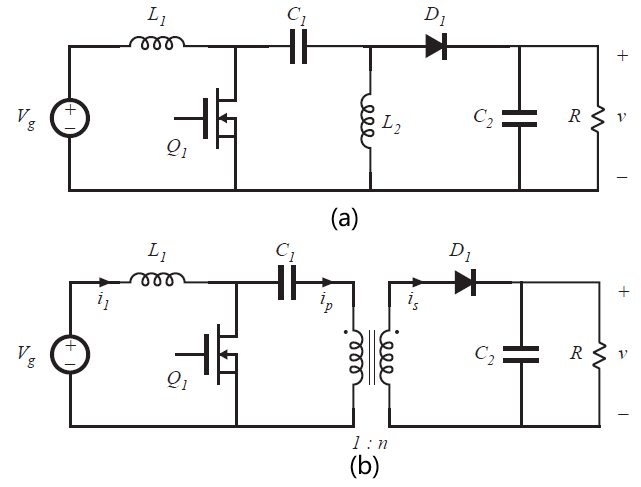
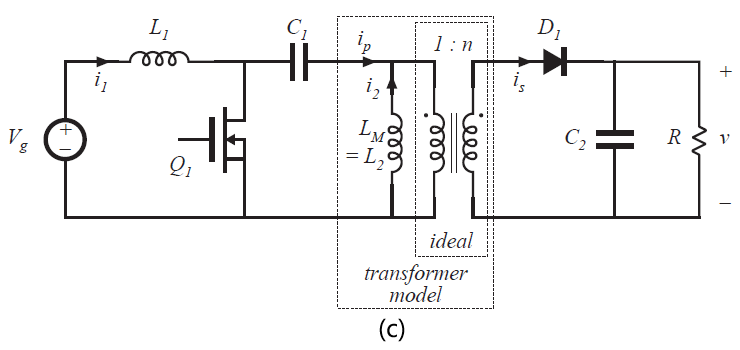
Fig 6.37 Obtaining isolation in the SEPIC: (a) basic nonisolated converter, (b) isolated SEPIC, (c) with transformer equivalent circuit model.

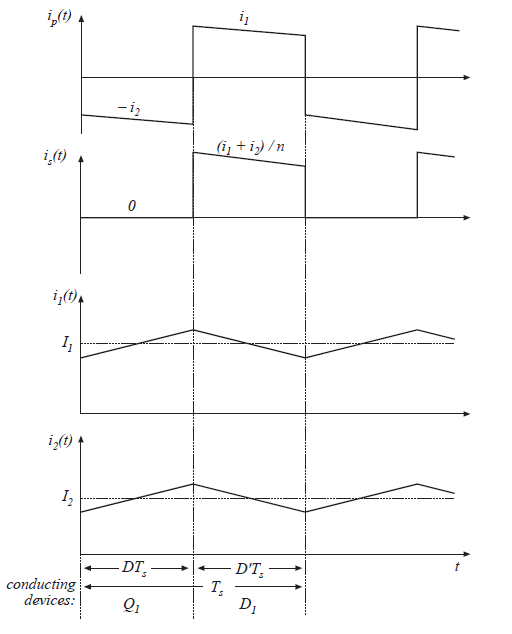
Fig 6.38 Waveforms of the isolated SEPIC, continuous conduction mode.

连续导通模式下，典型的初级以及次级绕组电流波形\(i_{p}(t)\)和\(i_{s}(t)\)如图6.38所示。磁性元件必须既充当反激变压器，又必须充当常规的双绕组变压器。在子区间1内，晶体管\(Q_{1}\)导通，励磁电流流过初级绕组，次级电流为0。在子区间2内，二极管\(D_{1}\)导通，励磁电流流过次级绕组至负载。此外，输入电感电流\(i_{1}\)流过初级绕组。这就引起了次级电流\(i_{1}/n\)的附加分量，其同样流过负载。因此，SEPIC变压器的设计并不寻常，并且绕组电流的均方根（有效值）大于反激变压器的均方根（有效值）电流。

通过对电感\(L_{1}\)和\(L_{M}\)应用伏秒平衡，可以得到变换比：

\[M(D)=\frac{V}{V_{g}}=\frac{nD}{D^{'}} \tag{6.50} \]

理想情况下，晶体管必须阻断电压\(V_{g}/D^{'}\)。实际上，变压器漏感带来的振铃会导致额外的电压尖峰。反向隔离型SEPIC电路如图6.39所示。变压器的工作和设计与SEPIC相似。

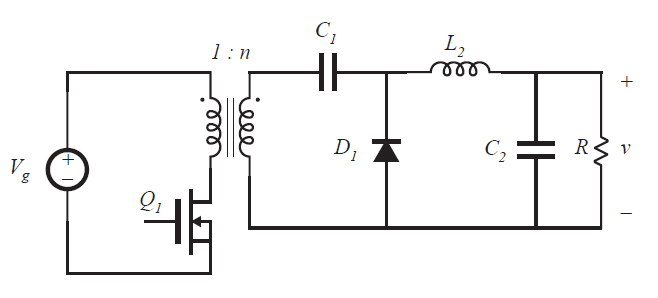
Fig 6.39 Isolated inverse-SEPIC

隔离Cuk变换器以不同的方式得到。基本非隔离Cuk变换器如图6.40(a)所示。在图6.40(b)中，电容\(C_{1}\)分裂为电容\(C_{1a}\)和\(C_{1b}\)的串联。在电容之间可以插入一个变压器，如图6.40(c)所示。为获得正的输出电压，将同名端反向连接。将电容与变压器的初级和次级绕组的连接可以使得没有直流电压施加到变压器。变压器以常规形式工作，磁化电流较小，在磁化电感中存储的能量可以忽略不计。

Cuk变换器中变压器的利用率非常好。励磁电流可以为正也可以为负，因此，如果合理设计，整个\(B-H\)环都可以使用。没有中心抽头，所有绕组都得到了充分的利用。晶体管必须阻断的电压为\(V_{g}/D^{'}\)，再加上一些由于变压器漏感引起的电压尖峰。变换器的变换比与式6.50表示的隔离型SEPIC变换器相同。

隔离型SEPIC和Cuk变换器可以用作开关电源，通常功率为几百瓦。现在也被用作AC-DC低谐波整流器。

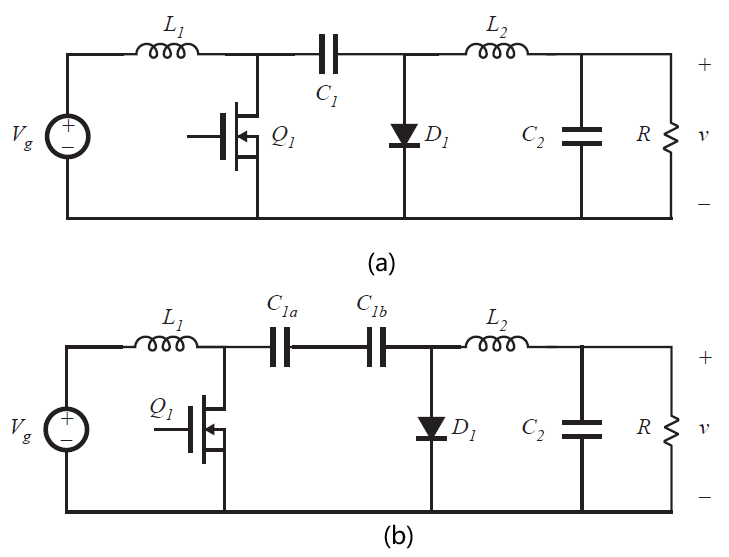
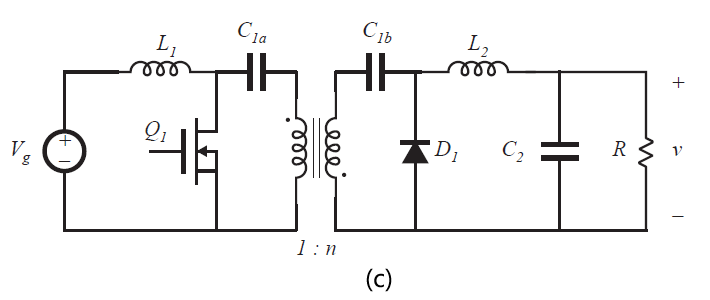
Fig 6.40 Obtaining isolation in the Cuk converter: (a) basic nonisolated Cuk converter, (b) splitting capacitor \(C_{1}\) into two series capacitors, (c) insertion of transformer between capacitors,