[Fundamental of Power Electronics]-PART I-6.变换器电路-6.1 电路演化

6.1 电路演化

第一章使用基本原理构建了buck变换器（图6.1）。开关可以降低电压直流分量，低通滤波器可消除开关纹波。在CCM下，buck变换器的变换比为\(M=D\)。buck变换器是最简单的，最基础的电路，我们将从这个电路得出其他电路。

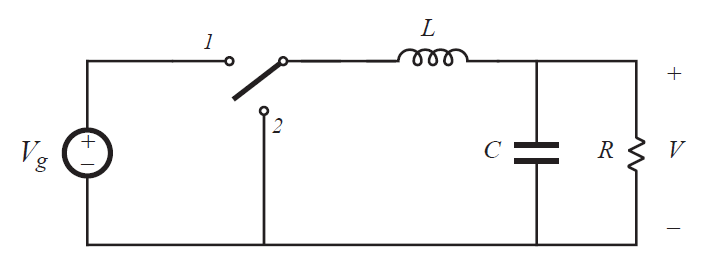
Fig 6.1 The basic buck converter

6.1.1 源荷反转

让我们首先考虑一下，如果将变换器的电源输入端口和电源输出端口互换会出现什么情况。在图6.2(a)的buck变换器中，电压\(V_{1}\)施加在端口1，电压\(V_{2}\)出现在端口2。我们知道：

\[V_{2}=DV_{1} \tag{6.1} \]

这个方程可以假设变换器工作在CCM下，通过电感伏秒平衡推导。假设开关实现能够使其成立，那么式6.1就是正确的，并且与电流流动方向无关。

所以，如图6.2(b)所示，我们互换电源与负载。通过电容旁路的负载连接到变换器的端口1，而电源连接到变换器端口2。现在功率以相反的方向流过变换器。式6.1必然是成立的，从而求取负载电压\(V_{1}\)可以得到：

\[V_{1}=\frac{1}{D}V_{2} \tag{6.2} \]

因此，负载电压大于电源电压。图6.2(b)反向看过来就是一个升压变换器。式6.2与我们熟悉的boost变换器结果几乎一致\(M(D)=1/D^{'}\)，只不过就是用\(D\)代替了\(D^{'}\)。

由于功率沿反方向流动，因此标准buck变换器的单向开关实现方式不能在图6.2(b)中使用。通过对第四章的讨论，我们发现可以通过在电感与地之间连接一个晶体管，在电感与负载之间连接一个二极管来实现这个开关的功能，如图6.2(c)所示。因此，晶体管的占空比\(D\)变为了图6.2(b)的单刀双掷(SPDT)开关在位置2上导通的时间而不是位置1上导通的时间。所以我们应该在式6.2中将\(D\)换为其互补值\(D^{'}\)。（译者：这里意思是，按直接反转源荷来看，boost变换器的电压变换率应该为1/D，但这里的D实际上在图6.2(b)中对应的是二极管的导通时间，真实的boost变换器中，这个位置是二极管，因此，实际的电压变换比为1/(1-D)。）

\[V_{1}=\frac{1}{D^{'}}V_{2} \tag{6.3} \]

因此，boost变换器可以看做是buck变换器的源荷反转得到，并且其中以允许功率流反向反转的方式来实现开关。

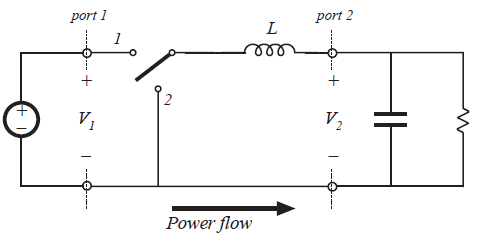
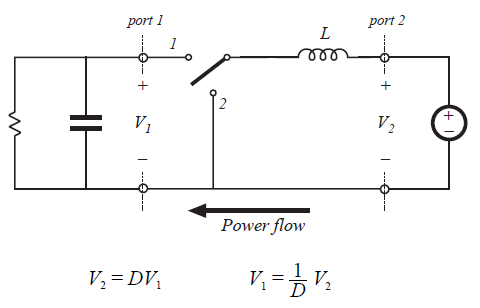
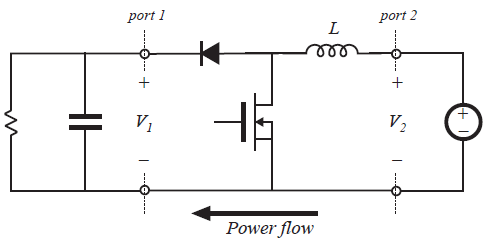
Fig 6.2 Inversion of source and load transforms a buck converter into a boost converter

6.1.2 变换器级联

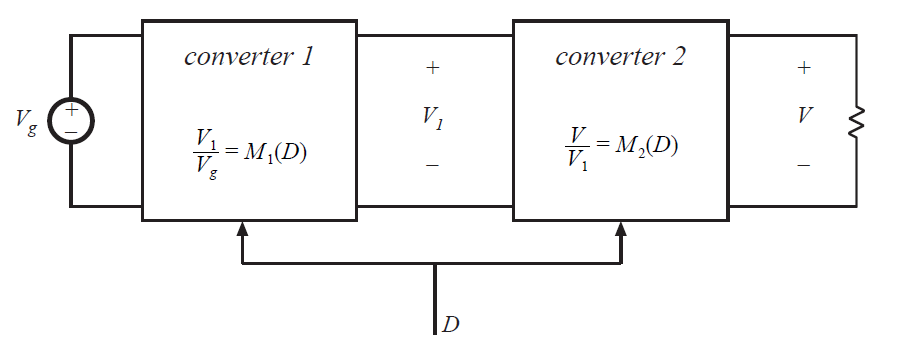
Fig 6.3 Cascaded connection of converters.

如图6.3所示，变换器也可以级联连接。变换器1的变比为\(M_{1}(D)\)，因此其输出电压\(V_{1}\)为：

\[V_{1}=M_{1}(D)V_{g} \tag{6.4} \]

这个电压施加在第二个变换器的输入端口。让我们假设第二个变换器与变换器1有相同的占空比\(D\)。如果变换器2的变换比为\(M_{2}(D)\)，那么输出电压\(V\)是：

\[V=M_{2}(D)V_{1} \tag{6.5} \]

将式6.4代入6.5可以得到：

\[\frac{V}{V_{g}}=M(D)=M_{1}(D) M_{2}(D) \tag{6.6} \]

因此，这个复合变换器的电压变换比\(M(D)\)为独立变比\(M_{1}(D)\)和\(M_{2}(D)\)的乘积。

让我们考虑这个情况，变换器1为buck，变换器2为boost变换器。复合变换器电路如图6.4所示。buck变换器电压变换比为：

\[\frac{V_{1}}{V_{g}}=D \tag{6.7} \]

boost变换器的电压变换比为：

\[\frac{V}{V_{1}}=\frac{1}{1-D} \tag{6.8} \]

所以复合变比应该为：

\[\frac{V}{V_{g}}=\frac{D}{1-D} \tag{6.9} \]

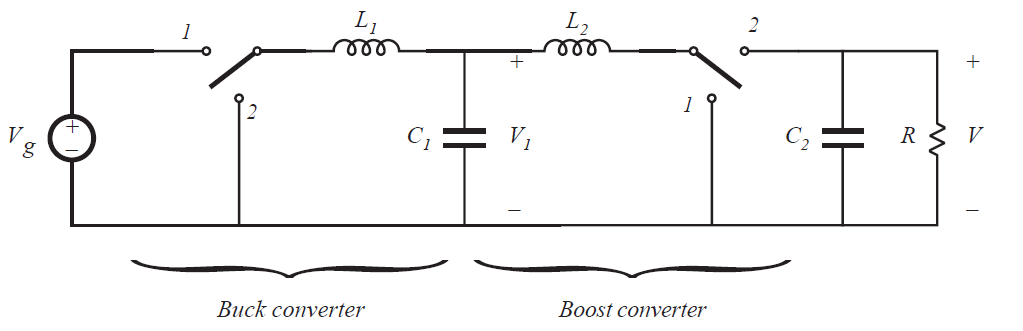
Fig 6.4 Cascade connection of buck converter and boost converter

该复合变换器具有同相降压-升压变换比。当\(D<0.5\)时电压下降，\(时D>0.5时\)电压上升。

图6.4所示的电路可以进行大大的简化。请注意，电感\(L_{1}\)，\(L_{2}\)和电容\(C_{1}\)构成了一个三极点低通滤波器。变换比并不取决于低通滤波器中极点的个数，因此当我们使用简单的低通滤波器时，应该会获得相同的稳态输出电压。在图6.5(a)中，电容\(C_{1}\)被移除了。电感\(L_{1}\)和\(L_{2}\)直接串联，因此可以合并为图6.5(b)所示的单电感。这个同相的降压-升压变换器仍然具有式6.9给出的电压变换比。

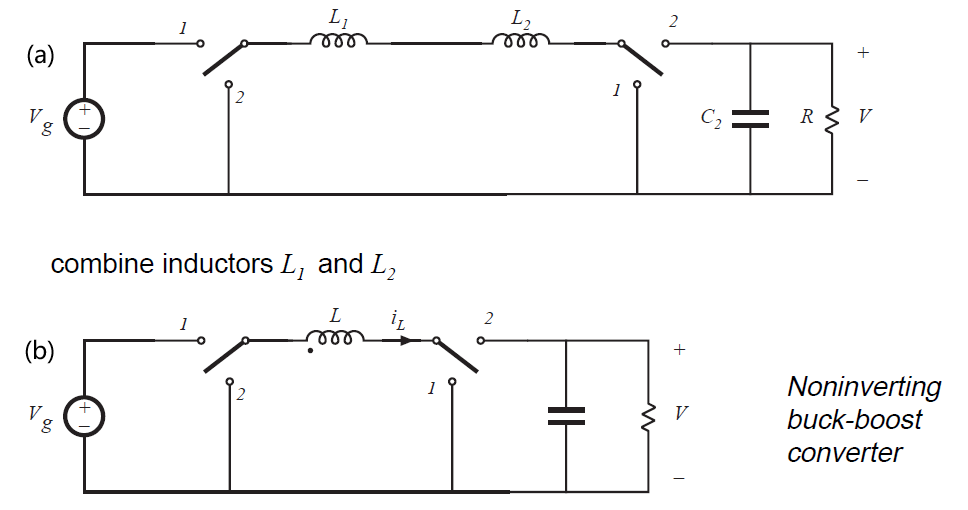
Fig 6.5 Simplification of the cascaded buck and boost converter circuit of Fig 6.4：(a) removal of capacitor \(C_{1}\). (b) combining of inductors \(L_{1}\) and \(L_{2}\).

图6.5(b)中的开关仍然可以简化，从而实现一个负的输出电压。当开关位于位置1时，变换器电路退化为图6.6(a)。电感连接到输入电源\(V_{g}\)，同时能量从电源流向电感。当开关位于位置2时，变换器退化为图6.6(b)。电感连接到负载，并且能量由电感传递到负载。为了获得一个负的输出，我们可以简单地在一个子区间内反转电感的极性(例如在开关位于位置2时)。然后获得图6.7所示的电路，并且变换率为：

\[\frac{V}{V_{g}}=- \frac{D}{1-D} \tag{6.10} \]

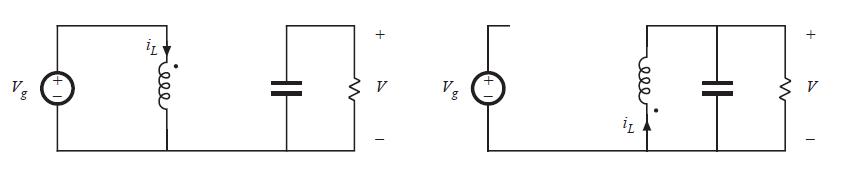
Fig 6.6 Connections of the circuit of Fig 6.5(b) :(a) left;while the switched are in position 1. (b)right; while the switches are in position 2.

Fig 6.7 Reversal of the output voltage polarity. By reversing the inductor connections while the switches are in position 2:(a)left; connections with the switches in position 2, (b)right; connections with the switches in position 2.

值得注意的是，电感的一侧现在始终接地，而另一侧在输入电源与负载之间切换。因此只需要一个SPDT开关就可以获得图6.8所示的变换器电路。图6.8被认为是常规（conventional）的buck-boost变换器。

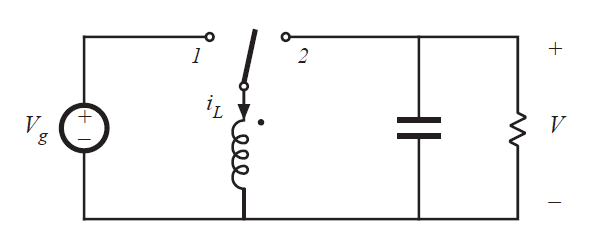
Fig 6.8 Converter circuit obtained from the subcircuits of Fig 6.7.

因此，buck-boost变换器可以看做是buck变换器和boost变换器的级联。buck-boost变换器的特性也与此观点相符合。实际上，buck-boost变换器的等效电路模型包含一个\(1:D\)的（降压）直流变压器，然后是一个\(D^{'}:1\)的（升压）直流变压器。buck-boost变换器继承了buck变换器的脉动输入电流和boost变换器的脉动输出电流。

其他变换器也可以通过级联得到。Cuk变换器（图2.20）实际上就是由boost变换器后接一个buck变换器。负的输出电压可以通过在子区间之一内将电容连接的极性进行反转；其与buck-boost变换器相同，这种操作具有减小开关数量的好处。Cuk变换器的等效电路模型主要包括一个\(：D^{'}：1\)的升压理想直流变压器，后跟一个\(1:D\)的（降压）理想直流变压器。Cuk变换器继承了boost变换器的无脉动输入电流属性和buck变换器的无脉动输出电流属性。

6.1.3 三端口单元旋转

buck，boost和buck-boost变换器电路中均含有一个连接SPDT（单刀双掷）开关的电感。如图6.9(a)所示，电感-开关网络可以视作标记为a，b，c的三端基本元件。在[1,2]中首次提出了这个观点，并且文献[3]指出，有三种不同的方法可以在电源和负载中连接这个单元。（译者：参考文献请查阅本书原文）连接a-A,b-B，c-C便成了buck变换器。连接a-C，b-A，c-B相当于源荷反转，便成了boost变换器。连接a-A，b-C，c-B便成了buck-boost变换器。因此，可以将buck，boost和buck-boost变换器视为基于相同电感-开关网络基本单元，但具有不同的源荷连接。

如图6.9(b)所示，一个双三端网络(dual three-terminal network)包含一个电容和开关单元。滤波电感与电源与负载串联连接，使得变换器的输入输出电流平滑无脉动。这里仍有三种方式可以在源荷之间连接该三端单元。连接a-A，b-B，c-C便成了一个具有LC低通滤波的buck变换器。连接a-B，b-A，c-C时相当于源荷反转，使其变为具有额外输出LC滤波的boost变换器。连接a-A，b-C，c-B便成了Cuk变换器。

在文献[4]中探讨了更加复杂的三端单元的旋转。

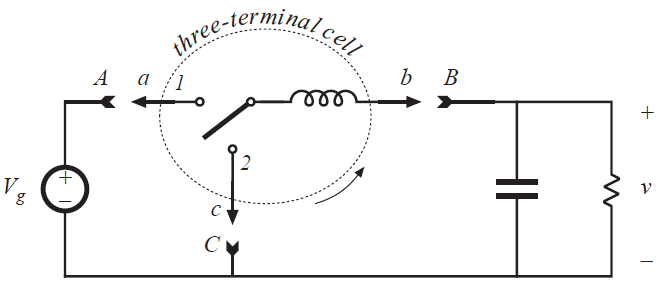
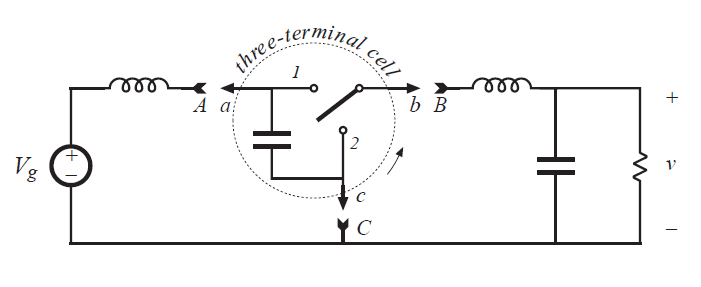
Fig 6.9 Rotation of three-terminal switch cells:(a) switch/inductor cell,(b)switch/capacitor cell.

6.1.4 负载差分连接

在需要交流输出的逆变器应用中，需要能够产生任一极性输出电压的变换器。通过合适的方式改变占空比，可以获得没有直流偏置的正弦输出电压。在本章到目前研究为止的变换器中，buck和boost只能产生正的单极性输出电压，而buck-boost和Cuk变换器只能产生负的单极输出电压。那么我们如何得到产生双极性输出电压的变换器？

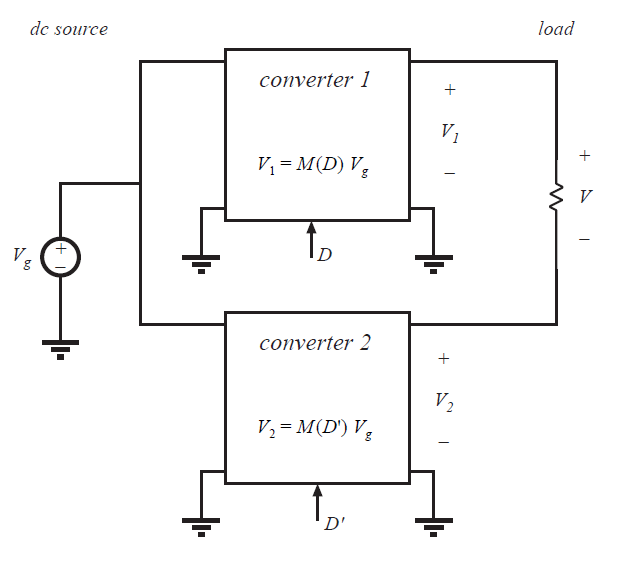
Fig 6.10 Obtaining a bipolar output by differential connection of load

获得双极性输出的一种众所周知的方法是负载在两个已知变换器的输出之间进行差分连接，如图6.10所示。如果变换器1产生电压\(V_{1}\)，变换器2产生电压\(V_{2}\)，那么负载电压\(V\)由下式给出：

\[V=V_{1}-V_{2} \tag{6.11} \]

尽管\(V_{1}\)和\(V_{2}\)可能会分别都是正值，但输出电压\(V\)是可能为正值或者负值的。典型的，如果变换器1的占空比为\(D\)，变换器2的占空比为其补数\(D^{'}\)，那么当\(V_{1}\)增加时，\(V_{2}\)下降，反之亦然（vice versa）。

使用差分连接的方式可以得到几个众所周知的逆变器电路。让我们使用buck变换器来实现图6.10中的变换器1和2。此时获得了图6.11(a)。变换器1的占空比为\(D\)，变换器2的占空比为其补数\(D^{'}\)。因此，当变换器1的SPDT开关位于上方位置时，变换器2的SPDT开关位于下方位置，反之亦然。变换器1输出电压\(V_{1}=DV_{g}\)，变换器输出电压为\(V_{2}=D^{'}V_{g}\)。差分负载电压为：

\[V=DV_{g}-D^{'}V_{g} \tag{6.12} \]

简化得到：

\[V=(2D-1)V_{g} \tag{6.13} \]

图6.12画出了该方程的曲线。从其中可以看到，当\(D>0.5\)时，输出电压为正，当\(D<0.5\)时，输出电压为负。如果占空比在0.5的静态工作点附近呈正弦变化，那么输出电压就是不含直流分量的正弦电压。

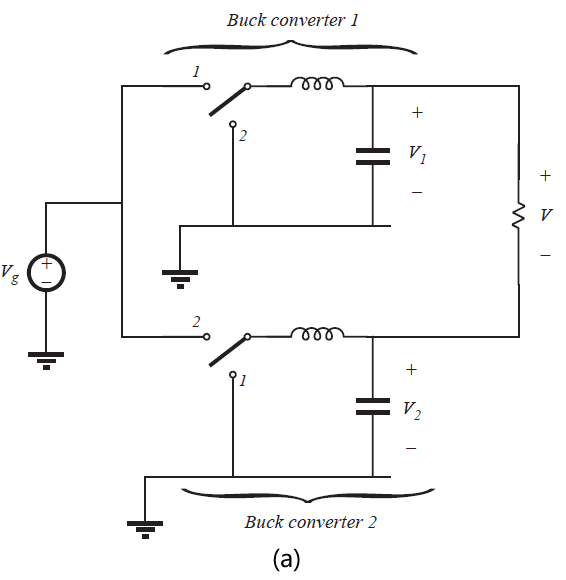
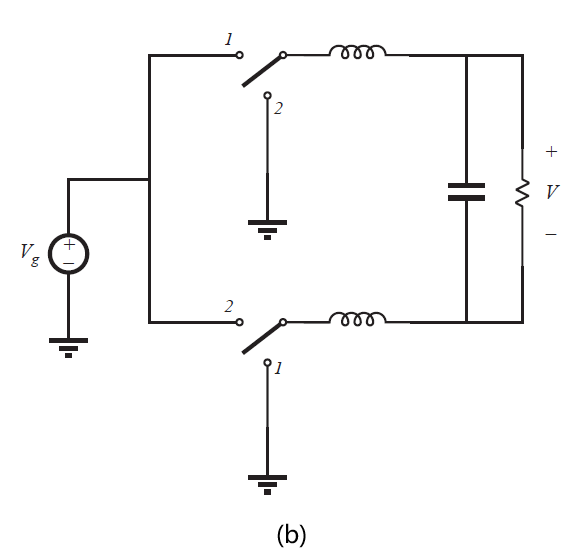
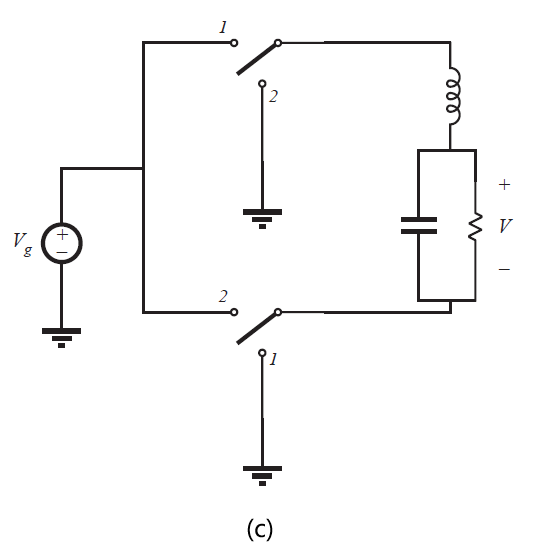
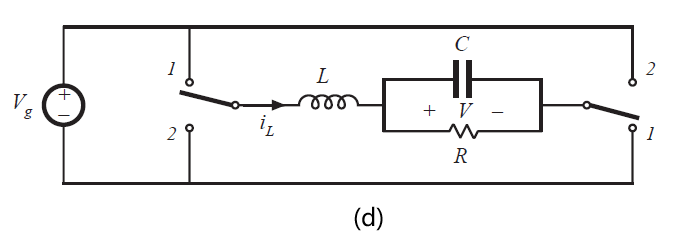
Fig 6.11 Derivation of bridge inverter(H-bridge): (a) differential connection of load across outputs of buck converters, (b) bypassing load by capacitor, (c) combining series inductors, (d) circuit (c) redrawn in its usual form.

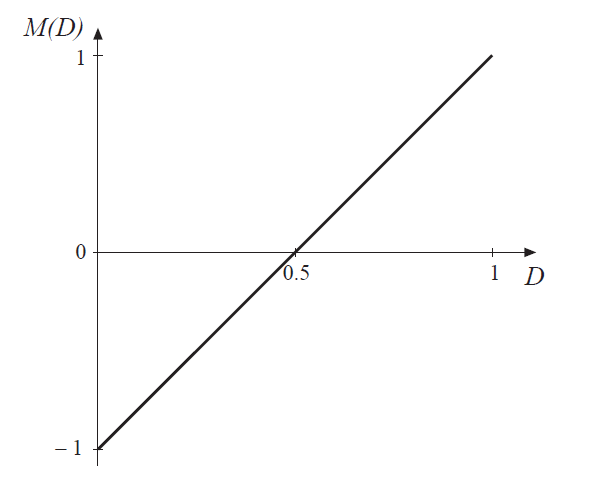
Fig 6.12 Conversion ratio of the H-bridge inverter circuit

图6.11(a)所示的电路可以简化。如图6.11(b)所示，通常设计为电容旁路负载。两个电感可等效为串联，合并为一个电感，如图6.11(c)所示。图6.11(d)等效于6.11(c)，但其更加简洁易懂。这个电路通常被称为H-bridge(H 桥电路)。它被广泛用于伺服放大器和单相逆变器中。其特性与buck变换器相似。

多相逆变器电路可以以同样的方式导出。如图6.12所示（译者：原文中即是这么编号的，有错误，这里不改正与其保持一致）三相负载可以通过差分连接于三个DC-DC变换器的输出。如果三相负载是平衡的，那么重点电压\(V_{n}\)将等于三个变换器输出电压的平均值：

\[V_{n}= \frac{1}{3}(V_{1}+V_{2}+V_{3}) \tag{6.14} \]

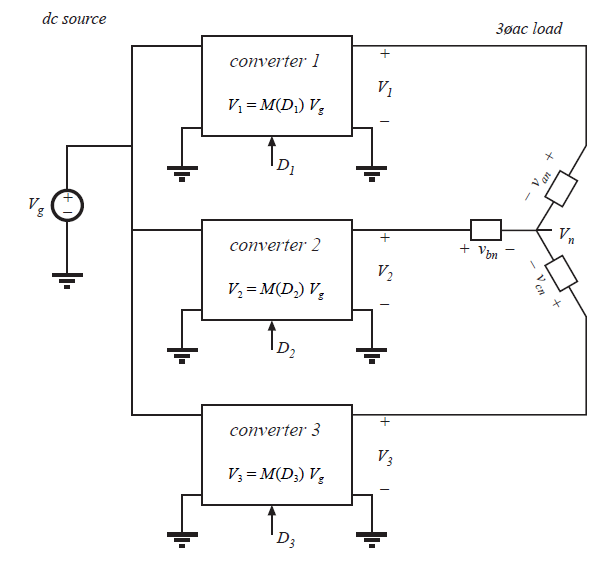
如果变换器输出电压\(V_{1}\)，\(V_{2}\)和\(V_{3}\)具有相同的直流偏置，那么这个偏置也会出现在中点电压\(V_{n}\)中。相电压\(V_{an}\)，\(V_{bn}\)和\(V_{cn}\)可以得到：

\[V_{an}=V_{1}-V_{n} \\ V_{bn}=V_{2}-V_{n} \\ V_{cn}=V_{3}-V_{n} \tag{6.15} \]

可以看到，直流偏置被抵消了，并且不会出现在\(V_{an}\)，\(V_{bn}\)和\(V_{cn}\)中。（译者：此处应该是线电压被抵消？）

让我们来用buck变换器实现图6.12中的变换器1,2和3。然后就获得了图6.13(a)。为了清晰简化，得到了6.13(b)。这个变换器有几个名字，包括电压源型逆变器和buck型三相桥式电路。基于buck变换器以外的DC-DC变换器的逆变器电路可以由类似的方式导出。图6.13(c)包含了具有boost型电压变换比的三相电流反馈（current-fed)桥式变换器，也被称为电流源逆变器。由于大多数逆变器应用都要求具有降低电压幅值的能力，因此通常在该逆变器的直流输入端上串联一个DC-DC buck变换器。三相逆变器的其他几个示例在[5-7]中给出，这些逆变器具有增加和减小电压幅值的能力。

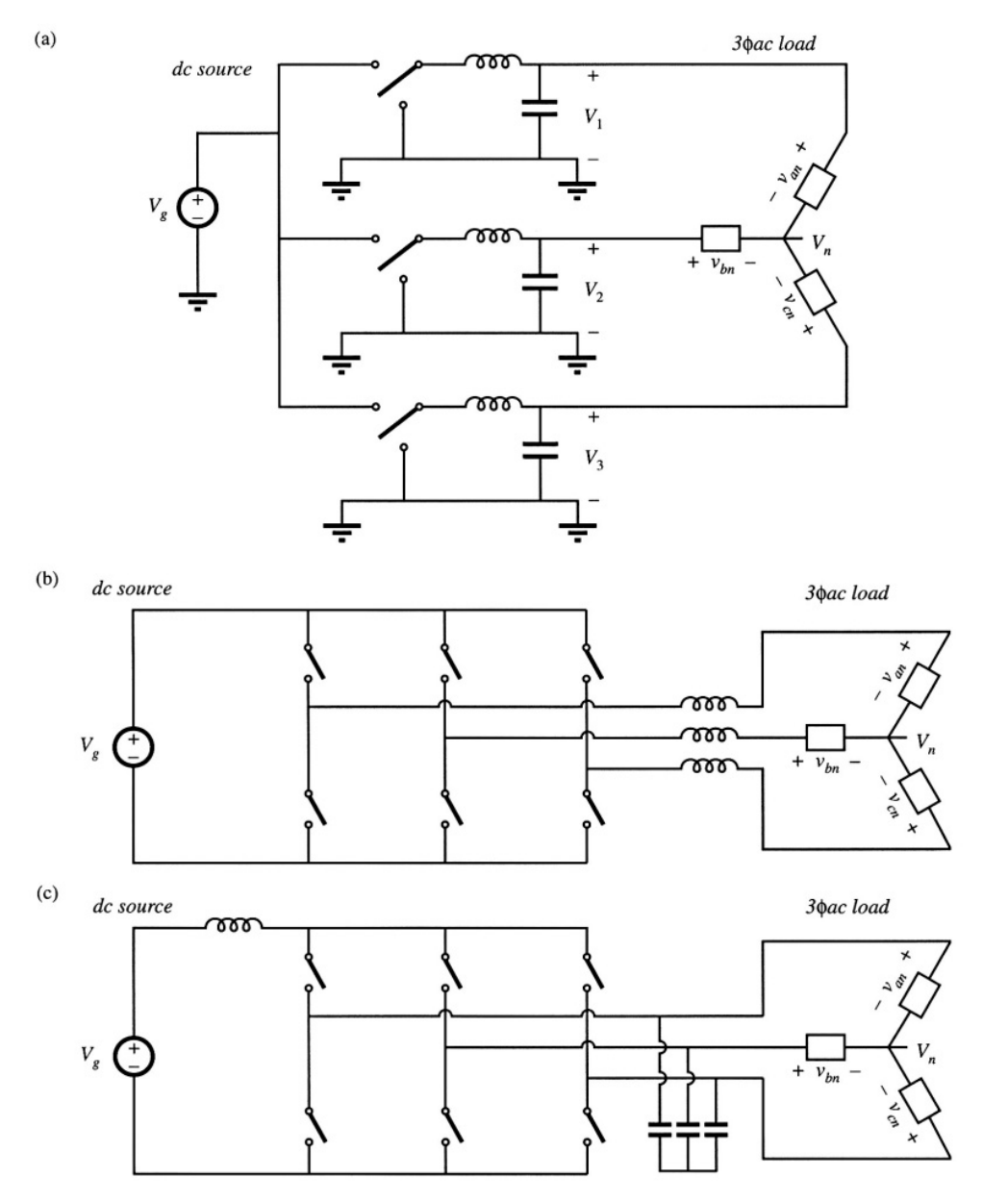
Fig 6.13 DC-3φ AC inverter topologies：(a) differential connection of 3φ load across outputs of buck converters: (b) simplification of low-pass filters to obtain the DC-3φ AC voltage-source inverter，(c) the DC-3φ AC current-source inverter.