[Fundamental of Power Electronics]-PART I-5.不连续导电模式-5.3 Boost变换器实例

5.3 Boost变换器实例

作为第二个示例，考虑图5.12的Boost变换器。让我们来确定不同模式的边界并且求解DCM下的电压变换比。此前在2.3节中分析了在CCM工作的Boost变换器的特性，并确定了电感电流直流分量$I$和纹波峰值幅度$\Delta i_{L}$的表达式。

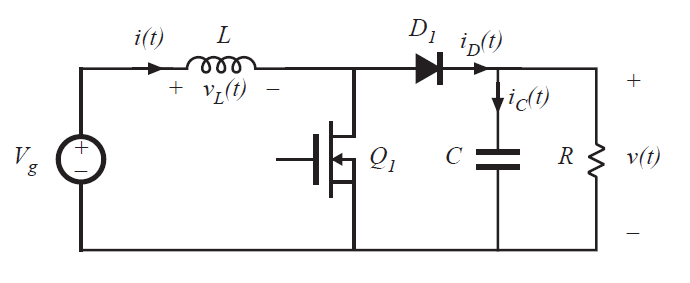
Fig 5.12 Boost converter example

当二极管导通时，其电流等于电感电流$i_{L}(t)$，从图2.18可以看出，电感电流的最小值在二极管导通间隔期间，$DT_{s}<t<T_{s}$，其值为$(I-\Delta i_{L})$。如果这个最小值是正的，那么二极管就会在整个子区间$DT_{s}<t<T_{s}$内正向偏置，并且变换器工作在CCM。因此，Boost变换器在CCM和DCM下运行的条件为：

$$I> \Delta i_{L} \ \ \ for \ CCM \\ I< \Delta i_{L} \ \ \ for \ DCM \tag{5.30}$$

这与buck变换器的结果是相同的。根据CCM时采用的分析方法（式2.39,2.43）求解$I$和$\Delta i_{L}$,得到：

$$\frac{V_{g}}{{D^{'}}^{2}R}>\frac{DT_{s}V_{g}}{2L} \ \ for \ CCM \ \ \tag{5.31}$$

对方程转换形式：

$$\frac{2L}{RT_{s}}>D{D^{'}}^{2} \ \ for \ CCM \tag{5.32}$$

写成标准形式为：

$$K>K_{crit}(D)\ \ for\ CCM \\ K<K_{crit}(D)\ \ for\ DCM \tag{5.33}$$

其中

$$K=\frac{2L}{RT_{s}}\ \ and\ \ K_{crit}(D)=D{D^{'}}^{2}$$

CCM和DCM下的工作条件与buck变换器的工作条件类似，但是其中的临界值$K_{crit}(D)$是占空比$D$的不同函数。$K_{crit}(D)$对占空比$D$的依赖关系如图5.13所示。$K_{crit}(D)$在$D=0$和$D=1$时为0，并且在占空比$D=1/3$时具有最大值$4/27$。因此，如果$K>4/27$，那么变换器对所有的$D$，都工作在CCM下。图5.14绘出了当$K<4/27$时的情况。变换器在$D=1/3$为中值的范围内以DCM运行。但变换器会在$D=0$和$D=1$附近以CCM运行。与buck变换器不同，boost变换器在$D=0$附近必须以CCM工作，这是由于纹波的幅值接近于0而直流分量$I$并不是。

Fig 5.13 Boost converter $K_{crit}(D)$ vs. $D$

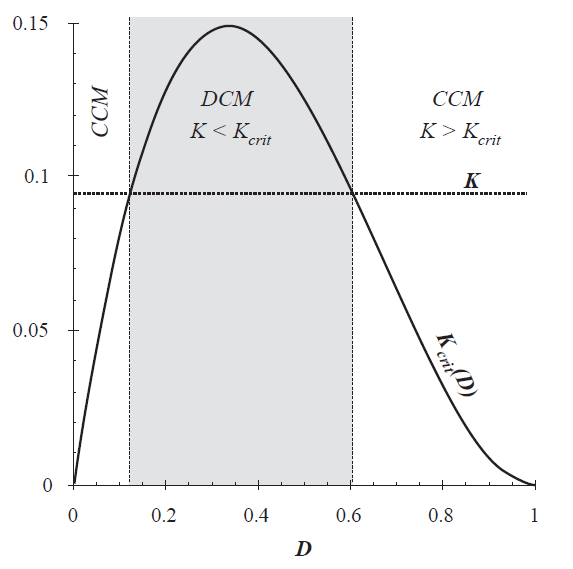
Fig 5.14 Comparison of K with $K_{crit}(D)$.

下一步，我们来分析Boost变换器的变换比$M=V/V_{g}$。在子区间$0<t<D_{1}T_{s}$内，晶体管导通，变换器退化为图5.15(a)所示的电路。电感电压和电容电流可以得到：

$$v_{L}(t)=V_{g} \\ i_{C}(t)=- \frac{v(t)}{R} \tag{5.34}$$

使用线性纹波近似，忽略输出电容电压的纹波，得到：

$$v_{L}(t) \approx V_{g} \\ i_{C}(T) \approx -\frac{V}{R} \tag{5.35}$$

在第二个子区间内$D_{1}T_{s}<t<(D_{1}+D_{2})T_{s}$，二极管导通，电路退化为图5.15(b)所示。电感电压与电容电流可由下式得到：

$$v_{L}(t)=V_{g}-v(t) \\ i_{C}(t)=i(t)-\frac{v(t)}{R} \tag{5.36}$$

忽略输出电容纹波可得到：

$$v_{L}(t) \approx V_{g}-V \\ i_{C}(t) \approx i_(t)-\frac{V}{R} \tag{5.37}$$

电感电流纹波不能忽略。

在第三个子区间$(D_{1}+D_{2})T_{s}<t<T_{s}$，晶体管和二极管都关断，电路如图5.15(c)所示，电路方程为：

$$v_{L}=0,i=0 \\ i_{C}(t)=-\frac{v(t)}{R} \tag{5.38}$$

采用小纹波近似得到：

$$v_{L}(t)=0 \\ i_{C}(t)=-\frac{V}{R} \tag{5.39}$$

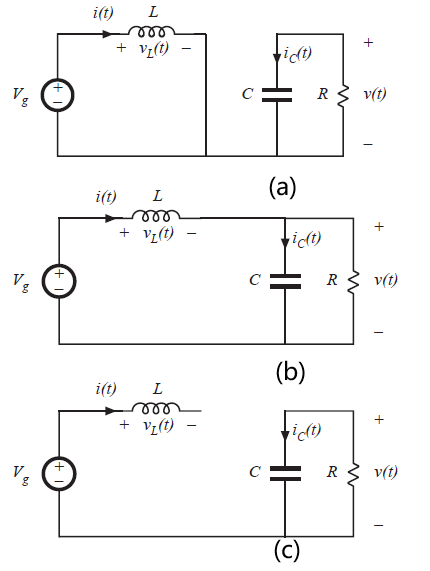
Fig 5.15 Boost converter circuits:(a) during subinterval 1 (b) during subinterval 2 (c)during subinterval 3

图5.16是通过式5.35,5.37和5.39描绘的电感电压波形。根据伏秒平衡，变换器在稳态下运行时，该波形的直流分量必须是0。通过令该波形的平均值等于0，可以得到：

$$D_{1}V_{g}+D_{2}(V_{g}-V)+D_{3}(0)=0 \tag{5.40}$$

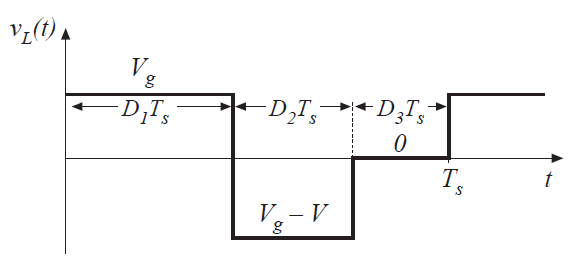
Fig 5.16 inductor voltage waveforms $v_{L}(t)$，boost converter operating in DCM

输出电压$V$为：

$$V=\frac{D_{1}+D_{2}}{D_{2}}V_{g} \tag{5.41}$$

二极管占空比$D_{2}$仍然是未知数，因此在求得输出电压$V$之前还需要第二个方程来消除$D_{2}$。

我们可以再次使用电容电荷平衡来获取第二个方程。输出电容与其相邻元件的连接如图5.17所示。与buck变换器不同，boost变换器中的二极管与输出节点相连。图5.17的节点方程可写为：

$$i_{D}(t)=i_{C}(t)+\frac{v(t)}{R} \tag{5.42}$$

其中$i_{D}(t)$是二极管电流。根据电容电荷平衡，电容电流$i_{C}(t)$在稳态下的直流分量必须是0。因此，二极管电流直流分量$<i_{D}>$必须与负载电流的直流分量相等：

$$<i_{D}>=\frac{V}{R} \tag{5.43}$$

因此我们需要描绘出二极管电流的波形，并且求出其直流分量。

Fig 5.17 Connection of the output capacitor to adjacent components in the boost converter

图5.18描绘了电感电流$i(t)$和二极管电流$i_{D}(t)$的波形。电感电流在第一个区间内，从零开始，上升到峰值电流$i_{pk}$。这个峰值电流等于斜率$V_{g}/L$乘以第一个区间长度$D_{1}T_{s}$：

$$i_{pk}=\frac{V_{g}}{L}D_{1}T_{s} \tag{5.44}$$

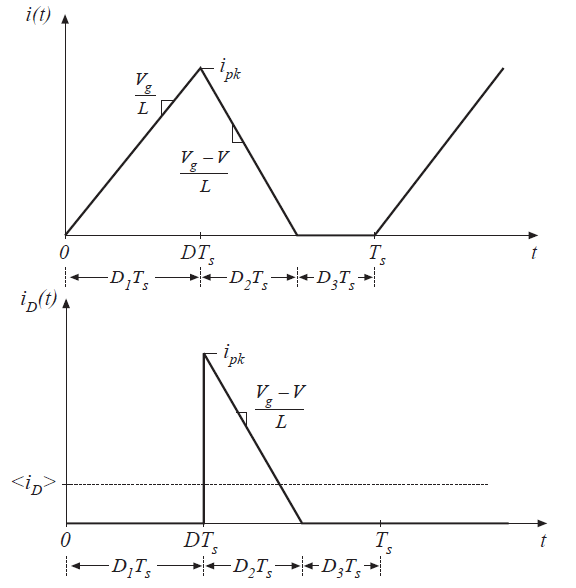
Fig 5.18 Boost converter waveforms in the DCM:(a) inductor current (b)diode current $i_{D}(t)$

二极管在第二个区间导通，电感电流减小到零，并且在第三个子区间保持不变。在第二个子区间内，二极管电流$i_{D}(t)$等于电感电流$i_{L}(t)$。在第一个和第三个子区间内，二极管反向偏置，因此其电流$i_{D}(t)$为0。

二极管电流的直流分量$<i_{D}>$为：

$$<i_{D}>= \frac{1}{T_{s}} \int _{0} ^{T_{s}} i_{D}(t)dt \tag{5.45}$$

这个积分值就是$i_{D}(t)$波形的面积。如图5.18(b)所示，这个面积就是以高为$i_{pk}$底为$D_{2}T_{s}$的三角形的面积：

$$\int _{0} ^{T_{s}} i_{D}(t)dt =\frac{1}{2}i_{pk} D_{2} T_{s} \tag{5.46}$$

将式5.44,5.46代入式5.45可以得到如下所示的二极管电流的直流分量表达式：

$$<i_{D}>=\frac{1}{T_{s}}(\frac{1}{2}i_{pk} D_{2} T_{s})=\frac{V_{g}D_{1}D_{2}T_{s}}{2L} \tag{5.47}$$

令上式与式5.43的负载电流直流分量表达式相等，可以得到最后的结果：

$$\frac{V_{g}D_{1}D_{2}T_{s}}{2L} =\frac{V}{R} \tag{5.48}$$

因此，这时我们有两个未知量$V$和$D_{2}$。有两个方程：根据电感伏秒平衡得到的式5.41和电容电荷平衡得到的5.48。联立方程可以消去$D_{2}$并且求解出输出电压$V$。根据式5.41解出$D_{2}$为：

$$D_{2}=D_{1} \frac{V_{g}}{V-V_{g}} \tag{5.49}$$

将这个结果插入式5.48，并且整理，可以得到下面所示的二次方程：

$$V^{2}-VV_{g}- \frac{{V_{g}}^2 {D_{1}}^2}{K}=0 \tag{5.50}$$

利用二次方程求根：

$$\frac{V}{V_{g}}=\frac{1±\sqrt{1+\cfrac{4{D_{1}}^{2}}{K}}}{2} \tag{5.51}$$

二次方程有两个根：式5.51中有一个根是正的，另一个是负的。我们已经知道，boost变换器输出电压的值一定是正的，并且实际上，根据式5.41可知，由于$D_1$和$D_{2}$均为正的，因此$V/V_{g}$也必须是正的。所以我们选择正的根：

$$\frac{V}{V_{g}}=M(D_{1},K)=\frac{1+\sqrt{1+\cfrac{4{D_{1}}^{2}}{K}}}{2} \tag{5.52} \\where\ \ \ K=2L/RT_{s} \\valid\ for \ \ \ K<K_{crit}(D)$$

这就是boost变换器工作在DCM下的解。

完整的Boost变换器输出特性（包括CCM和DCM）为：

$$M=\begin{cases}\cfrac{1}{1-D} \ \ \ for\ K>K_{crit} \\\cfrac{1+\sqrt{1+\cfrac{4{D_{1}}^{2}}{K}}}{2} \ \ for\ K<K_{crit}\end{cases}\tag{5.53}$$

对于不同$K$值的特性在图5.19中绘出。与buck变换器中一样，DCM可以使输出电压增加。并且特性曲线中DCM部分几乎都是线性的，可以被近似为：

$$M \approx \frac{1}{2}+\frac{D}{\sqrt{K}} \tag{5.54}$$

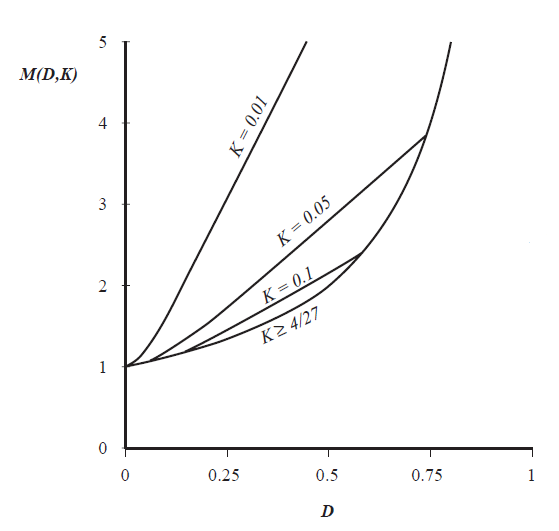
Fig 5.19 Voltage conversion ratio $M(D,K)$ of boost converter, including both continuous and discontinuous conduction modes.