[Fundamental of Power Electronics]-PART I-3.稳态等效电路建模，损耗和效率-3.5/3.6 示例：Boost变换器中包含的半导体传导损耗/要点小结

3.5 示例：Boost变换器中包含的半导体传导损耗

作为最后一个示例，让我们考虑对图3.22所示的Boost变换器中的半导体传导损耗进行建模。功率损耗的另一个主要来源是半导体器件的正向电压降引起的传导损耗。金属氧化物场效应晶体管(MOSFET)或双极结型晶体管(BJT)的导通压降可以以合理建模为导通电阻\(R_{on}\)。如果是二极管，绝缘栅双极型晶体管(IGBT)或晶闸管，则电压源加上导通电阻会得到精度非常高的模型；如果在单个工作点对变换器建模，则可以省略导通电阻。

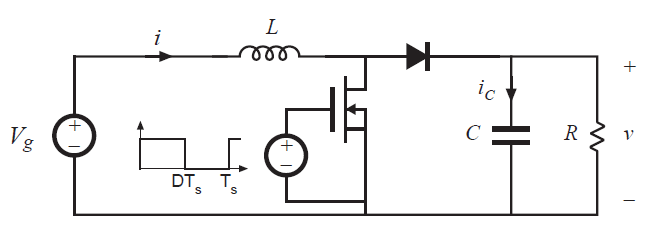
Fig 3.22 Boost converter example

当栅极驱动信号为高时，MOSFET导通且二极管反向偏置。电路简化为位置1处的电路。在导通状态下，MOSFET以导通电阻建模为\(R_{on}\)。电感绕组电阻再次如图3.5所示，电感电压和电容电流为：

\[v_{L}(t) = V_{g}-iR_{L}-iR_{on} \approx V_{g}-IR_{L}-IR_{on} \\ i_{C}(t) = -\frac{v}{R} \approx -\frac{V}{R} \tag{3.27} \]

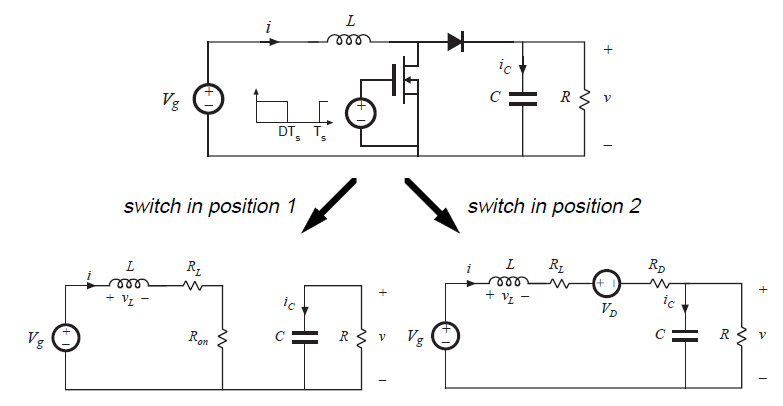
Fig 3.23 Boost converter circuit

电感电流和电容电压再次近似为其直流分量。

当栅极驱动信号为低时，MOSFET关断。二极管因电感电流而正偏，电路简化为上图位置2对应电路。这个例子中，二极管导通时被建模为电压源\(V_{D}\)和电阻\(R_{D}\)。电感绕组电阻仍为\(R_{L}\)。这个子区间内，电感电流以及电容电压为：

\[v_{L}(t) = V_{g}-iR_{L}-V_{D}-iR_{D}-v \approx V_{g} -IR_{L}-V_{D}-IR_{D}-V \\ i_{C}(t) = i- \frac{v}{R} \approx I- \frac{V}{R} \tag{3.28} \]

电感电压和电容电流波形如图3.24所示。

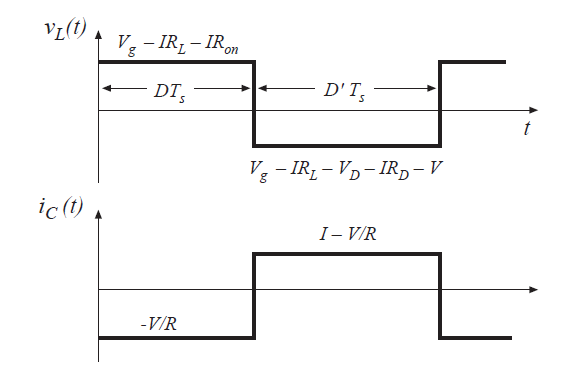
Fig 3.24 Inductor voltage and capacitor current

电感电压直流分量为：

\[<v_{L}> = D(V_{g}-IR_{L}-IR_{on})+D^{'}(V_{g}-IR_{L}-V_{D}-IR_{D}-V) = 0 \tag{3.29} \]

化简并利用\(D+D^{'}=1\)，得到

\[V_{g}-IR_{L}-IDR_{on}-D^{'}V_{D}-ID^{'}R_{D}-D^{'}V = 0 \tag{3.30} \]

该方程式描述了包含电感的环路各电压的直流分量，并且环路电流等于电感直流电流\(I\)。等效电路如图3.25所示。

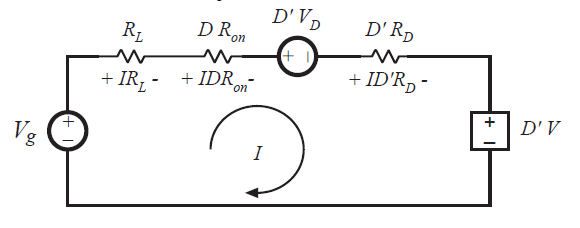
Fig 3.25 Equivalent circuit corresponding to equation (3.30)

电容电流的直流分量为：

\[<i_{C}>=D (-\frac{V}{R})+D^{'}(I-\frac{V}{R}) = 0 \tag{3.31} \]

化简可得：

\[D^{'}I - \frac{V}{R} = 0 \tag{3.32} \]

该方程式描述了流入电容器相连节点的电流直流分量，直流电容电压等于\(V\)。等效电路如图3.26所示：

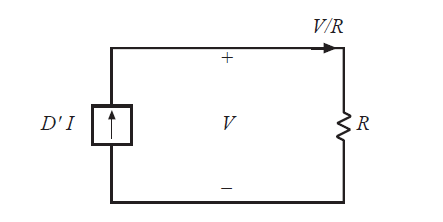
Fig 3.26 Equivalent circuit corresponding to equation (3.32)

上述两个电路在图3.27中组合为一个电路。如图3.28所示，将其中的从属电源变换为直流变压器，得到完整的直流等效电路模型。

Fig 3.27 The circuits of Fig 3.25 and 3.26，draw together

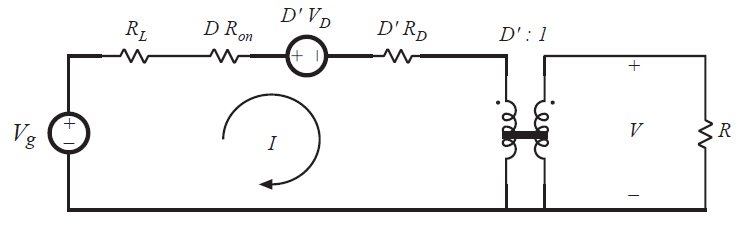
Fig 3.28 Equivalent circuit model of the boost converter

求解图3.28，输出电压\(V\)为：

\[V = (\frac{1}{D^{'}})(V_{g}-D^{'}V_{D})( \frac{D^{'2}R}{D^{'2}R +R_{L}+DR_{on}+D^{'}R_{D}}) \tag{3.33} \]

上式除以\(V_g\)得到电压变换比：

\[\frac{V}{V_{g}} = (\frac{1}{D^{'}})(1-\frac{D^{'}V_{D}}{V_{g}})( \frac{1}{1 + \frac{{R_{L}+DR_{on}+D^{'}R_{D}}}{D^{'2}R}}) \tag{3.34} \]

可以看到，损耗元素\(和V_{D},R_{D},R_{on} 和 R_{D}\)的影响是将电压变换比降至理想值\(1/D^{'}\)以下。

效率可以由\(\eta = P_{out}/P_{in}\)得到。由图3.28，\(P_{in}=V_{g}I\)以及\(P_{out}= VD^{'}I\)。因此：

\[\eta = D^{'} \frac{V}{V_{g}} ={ (1-\frac{D^{'}V_{D}}{V_{g}}) } /{( \frac{1}{1 + \frac{{R_{L}+DR_{on}+D^{'}R_{D}}}{D^{'2}R}})} \tag{3.35} \]

要想得到高效率，需要：

\[V_{g}/D^{'}>>V_{D} \\ D^{'2}R>>R_{L}+DR_{on}+D^{'}R_{D} \tag{3.36} \]

看起来很奇怪的是，图3.28所示的等效电路随着占空比变化的电阻有效值为\(DR_{on}\)和\(D^{'}R_{D}\)。这种依赖性关系的原因是只有当半导体器件导通时，才会在电路中连接各自的导通电阻。例如，当\(D=0\)时，MOSFET不会导通，有效电阻就会从模型中消失。这些有效电阻正确的模拟了元件中的平均功率损耗。例如，等效电路预测MOSFET的导通电阻功率损耗为\(I^{2}DR_{on}\)。而在实际电路中，MOSFET的导通损耗在MOSFET导通时为\(I^{2}R_{on}\)，关断时其为0。由于MOSFET以占空比\(D\)导通，因此平均导通损耗为\(DI^{2}R_{on}\)，与模型预测计算结果相一致。

通常，要计算电阻\(R\)中的功率损耗，我们必须计算通过电阻的均方根电流\(I_{rms}\)，而不是平均电流。然后平均功率损耗为\(I_{rms}^2R\)。但，如果电感电流的纹波很小，图3.28的平均模型可以正确预测平均功率损耗。例如，考虑Buck变换器中的MOSFET导通损耗。对于电感电流纹波\(\Delta i\)的几个不同值，实际管子流过电流波形如图3.29所示。情况(a)对应于采用无限大的电感\(L\)，使得电感电流纹波为0。如表3.1所示，MOSFET的传导损耗为\(I_{rms}^2R_{on}=DI^2R_{on}\)，这与平均模型的预测完全吻合。情况(b)选择电感的典型值，导致电感电流纹波为\(\Delta i = 0.1I\)。使用MOSFET电流的均方根值计算出的精确MOSFET导通损耗仅比平均模型的预测值大0.33％。在极端情况(c)中，\(\Delta i = I\)。实际传导损耗比平均模型预测的损耗大33％。因此，即使没有计算均方根电流，直流（平均）模型也可以正确预测元件非理想状态下的损耗。如果电感器电流纹波很小，则该模型是准确的。

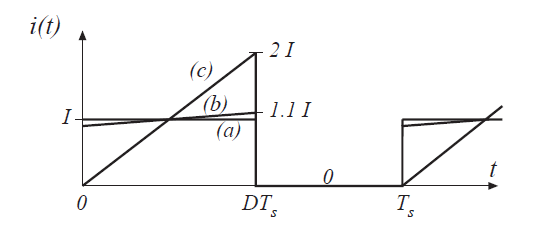
Fig 3.29 Transistor current waveform, for various filter inductor values a: with a very large inductor, such that $\Delta i \approx 0 $ . b: with a typical inductor value, such that \(\Delta i= 0.1I\) c: with a small inductor value .such that \(\Delta i = I\)

Table 3.1 Effect of inductor current ripple on MOSFET conduction loss

3.6 要点总结

1. 直流变压器模型代表任何DC-DC变换器的主要功能：理想地具有100%效率的直流电压和电流的变换，以及通过占空比\(D\)来控制的变换比\(M\)。这种模型易于使用常规电路分析的熟悉技术进行变换与求解。
2. 还可以对模型进行完善以解决诸如电感器绕组电阻，半导体导通电阻和正向压降之类的损耗因素。改进后的模型可以预测实际非理想变换器的电压，电流和效率。
3. 通常可以使用电感伏秒平衡和电容电荷平衡方程得到变换器的直流等效电路。当环路和节点方程与伏秒平衡与电荷平衡方程一致时可构建等效电路。在具有脉动输入电流的变换器中，需要额外的公式来对变换器输入端口进行建模，可以通过对变换器输入电流求平均来获得该方程。