[Fundamental of Power Electronics]-PART I-3.稳态等效电路建模，损耗和效率-3.4 如何获得模型的输入端口

3.4 如何获得模型的输入端口

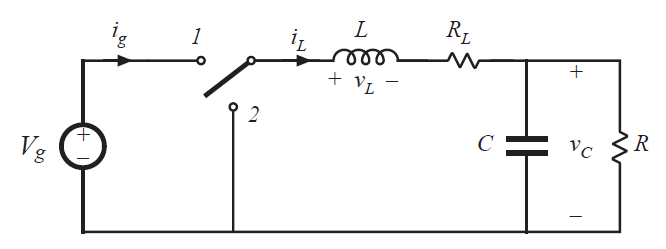
Fig 3.16 Buck converter example

让我们尝试使用3.3.3节的步骤来推导图3.16所示的Buck变换器的模型。电感绕组电阻同样由串联电阻\(R_{L}\)来代替

电感电压平均值表示为：

\[<v_{L}>=0 =DV_{g}-I_{L} R_{L}-V_{C} \tag{3.24} \]

该方程式描绘了一个具有直流电感电流\(I_{L}\)的环路。这个环路电压分别为：(1)从属电压源\(DV_{g}\)；(2)电阻\(R_{L}\)导致的电压降\(I_{L}R_{L}\)；(3)输出电压\(V_{C}\)。

电容电流平均值为：

\[<i_{C}>=0=I_{L}-\frac{V_{C}}{R} \tag{3.25} \]

该方程描述了流入连接到电容节点的直流电流。电感电流直流分量\(I_{L}\)流入节点，直流负载电流\(V_{C}/R\)流出节点。对等式(3.24)和(3.25)建模的等效电路由图3.17给出。这个电路可以求解直流输出电压\(V_{C}\)。

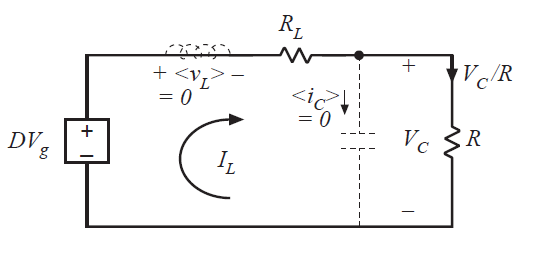
Fig 3.17 Equivalent circuit dervied from (3.24) and (3.25)

图3.17中的直流变压器发生了什么？我们期望Buck变换器的模型中包含一个直流变压器，且其匝比等于直流变换比，也就是\(1:D\)。根据图3.2，变压器的次级应该等效为一个值为\(DV_{g}\)的从属电压源。这样的次级确实出现在了图3.17中，但是问题在于，初级在什么地方？根据图3.2，我们期望直流变压器的初级等效为从属电流源。通常，要获得这个源，必须变换器输入电流\(i_{g}(t)\)的直流分量。

变换器的输入电流\(i_{g}(t)\)波形描绘在图3.18中。当开关位于位置1时，\(i_{g}(t)\)等于电感电流。忽略电感电流纹波，有\(i_{g}(t) \approx I_{L}\)。当开关位于位置2时，\(i_{g}(t)\)为0。所以，\(i_{g}(t)\)的直流分量或者说平均值为：

\[I_{g}= \frac{1}{T_{s}} \int _0 ^{T_{s}} i_{g}(t)dt = DI_{L} \tag{3.26} \]

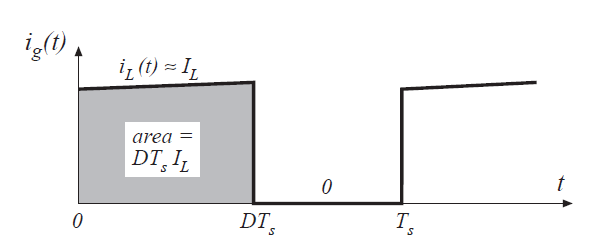
Fig 3.18 Input current waveform \(i_{g}(t)\)

\(i_{g}(t)\)的积分值等于其波形曲线包围的面积，根据图3.18也就是\(DT_{s}I_{L}\)。因此直流分量\(I_{g}\)就是\(DT_{s}I_{L}/T_{s}\)。公式(3.26)表明，变换器从电源\(V_{g}\)输出的电流直流分量\(I_{g}\)为\(DI_{L}\)。等效电路如图3.19所示。

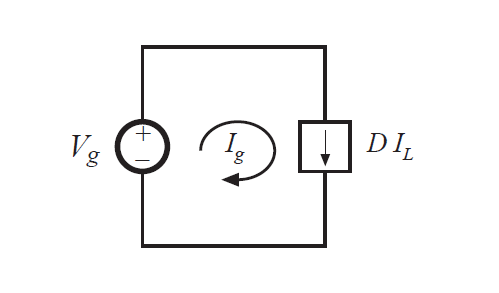
Fig 3.19 Input port equivalent circuit

现在可以通过结合图3.17和3.19获得图3.20所示的完整的Buck变换器的模型。从属电流和电压源可以结合为直流变压器，因为\(DV_{g}\)从属电压源是\(D\)乘以从属电流源两端的电压\(V_{g}\)，并且电流源同样是\(D\)乘以从属电压源两端的电流\(I_{L}\)。因此，根据图3.2，上述电源等效为具有匝比为\(1:D\)的直流变压器，如图3.21所示。

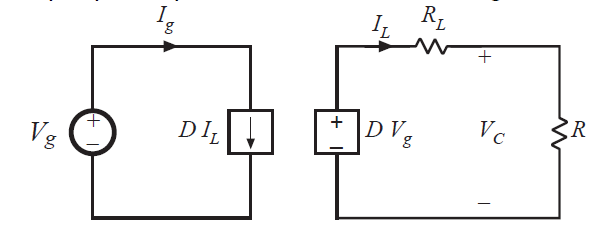
Fig 3.20 Input and output port equivalent circuits

Fig 3.21Replace dependent sources with equivalent dc transformer

通常，要获得对变换器输入端口建模的完整直流等效电路。必须为变换器的直流输入电流列写相应的方程，然后构造对应于该方程的等效电路。在Buck变换器以及具有脉动电流输入的其他变换器中，该等效电路包含一个从属电流源，该电流源成为直流变压器模型的主要部分。在3.3节中的Boost变换器的实例中，由于输入电流\(i_g (t)\)与电感电流\(i(t)\)一致，因此无需明确列写该方程。所以只用电感电压和电容电流方程就可以得完整的等效电路。