[Fundamental of Power Electronics]-PART I-3.稳态等效电路建模，损耗和效率-3.3 等效电路模型的构建

3.3 等效电路模型的构建

接下来，让我们完善直流变压器模型来解决变换器的损耗问题。这将使用众所周知的电路分析技术来确定变换器的电压，电流和效率。

在前面的章节，我们利用电感伏秒平衡和电容电荷平衡得到了式(3.11)和式(3.13)，这里我们重写：

\[<v_{L}> = 0 =V_{g} - IR_{L} -D^{'}V \\<i_{C}> = 0 =D^{'}I - \frac{V}{R} \tag{3.15} \]

这些方程表明，电感电压与电容电流的直流分量为0。与其像上一节那样利用代数方法求解方程式，不如根据这些方程式重新构建电路模型，该电路模型描述了具有铜损的Boost变换器直流特性。这是通过构造一个基尔霍夫回路和节点方程为式(3.15)的电路来完成的。

3.3.1 电感电压方程

\[<v_{L}> = 0 =V_{g} - IR_{L} -D^{'}V \tag{3.16} \]

这个公式是通过在每个子间隔内应用基尔霍夫电压定律得出的，以找到电感的电压。将结果取平均值并置零。式(3.16)表明三项的电压之和等于\(<v_{L}>\)，也就是0。因此，式(3.16)与环路方程的形式相同：特别是，它描述了含电感环路电压的直流分量，同时环路电流等于电感电流的直流分量。

因此，让我们来构建一个电路，这个电路包含一个电流为\(I\)的环路，对应于方程(3.16)。其第一项为直流输入电压\(V_{g}\)，所以在图3.10中我们要包含值为\(V_{g}\)的电压源。第二项是与回路电流成正比的电压降的值\(IR_{L}\)，第三项是一个取决于变换器输出电压的电压值\(D^{'}V\)。现在我们可以使用独立电压源来进行建模，其极性根据式(3.16)来确定。

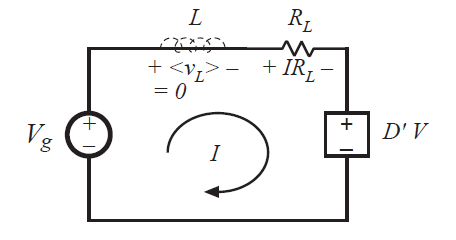
Fig 3.10 Inductor voltage equation

3.3.2 电容电流方程

\[<i_{C}> = 0 =D^{'}I - \frac{V}{R} \tag{3.17} \]

这个方程是在每个子区间内运用基尔霍夫电流定律推导求得电容电流。将结果平均，并将平均电容电流置零。

式(3.17)表明两个直流电流之和等于\(<i_{C}>\)，或者说是0。因此，式(3.17)与节点方程形式相同。特别是，它描述了与电容连接节点的电流的直流分量。直流电压电压为\(V\)。

现在让我们来构建一个如图3.11所示的包含连接到电容的节点的一个电路，并且其节点方程满足(3.17)。方程的第二项是电流幅值\(V/R\)，正比于电容直流电压。这一项对应着一个与电容并联的电阻，所以它的电压是\(V\)，电流为\(V/R\)。第一项是取决于电感直流电流\(I\)的电流\(D^{'}I\)。现在我们可以使用如图所示的相关电流源对该项进行建模，并且其极性根据式(3.17)确定。

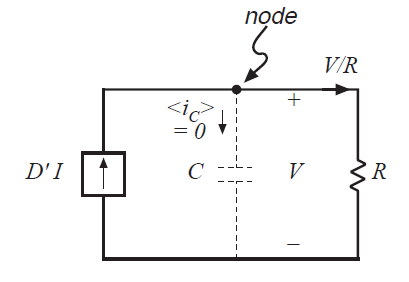
Fig 3.11 Capacitor current equation

3.3.3 完整电路模型

下一步就是结合图3.10和3.11所示的电路形成图3.12所示的单个电路。如第3.1节所述，可以通过将相关电压和电流源构成理想的直流变压器进一步简化该电路。与\(D^{'}V\)相关的从属电压源（译者：可能为从属电压源，受控电压源）取决于从属电流源两端的电压\(V\)。同样的，从属电流源\(D^{'}I\)取决于流过从属电压源的电流\(I\)。在这每种情况下，系数均为\(D^{'}\)。因此，从属电源形成类似图3.2所示的电路(即3.12所示）。由于变压器的对称性，电压源出现在初级侧还是次级侧并没有那么重要。因此他们等效于3.3所示的匝比为\(D^{'}:1\)的直流变压器模型。用理想的直流变压器模型代替从属电源可得到图3.13的等效电路。

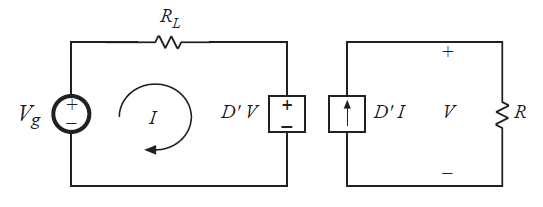
Fig 3.12 The two circuits, drawn together

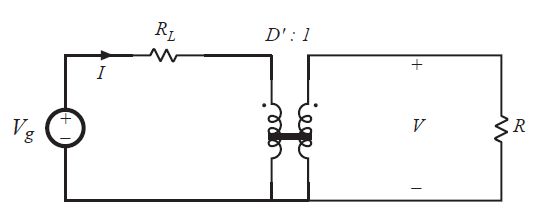
Fig 3.13 The dependent sources are equivalent to a D’ : 1 transformer

等效模型现在可以用来求解变换器电压和电流。例如，我们可以通过将电压源\(V_{g}\)和电阻\(R_{L}\)引入次级侧来消除变压器。如图3.14所示，电压源的值除以有效匝数比\(D^{'}\)，电阻\(R_{L}\)除以匝比的平方\(D^{'2}\)。利用分压公式可以直接针对输出电压求解该电路：

\[V = \frac{V_{g}}{D^{'}} \frac{R}{R+ \frac{R_{L}}{D^{'2}}} =\frac{V_{g}}{D^{'}} \frac{1}{1+ \frac{R_{L}}{D^{'2}R}} \tag{3.18} \]

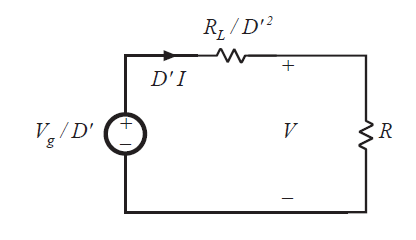
Fig 3.14 Refer all elements to transformer secondary

该结果与式(3.14)相同。这个电路也可以通过将所有元件变换到初级侧来直接求解电感电流\(I\)。结果是：

\[I = \frac{V_{g}}{D^{'2}R +R_{L}}=\frac{V_{g}}{D^{'2}R} \frac{1}{1+ \frac{R_{L}}{D^{'2}R}} \tag{3.19} \]

3.3.4 效率

变换器的等效电路还允许我们计算变换器的效率\(\eta\)。根据图3.13得到输入功率为：

\[P_{in}= V_{g}I \tag{3.20} \]

负载电流等于理想直流变压器次级侧线圈中的电流，或者表示为\(D^{'}I\)。因此，模型可以预测到变换器的输出功率为：

\[P_{out} = V(D^{'}I) \tag{3.21} \]

因此变换器的效率为：

\[\eta = \frac{P_{out}}{P_{in}} = \frac{V(D^{'}I)}{V_{g}I} = \frac{V}{V_{g}}D^{'} \tag{3.22} \]

将式(3.18)代入式(3.22)，消去\(V\)，得到：

\[\eta = \frac{1}{1+ \frac{R_{L}}{D^{'2}R}} \tag{3.23} \]

在不同的\(R_{L}/R\)的值下，上式对应曲线如图3.15所示。从式(3.23)可以看出，要获得很高的效率，电感绕组电阻\(R_{L}\)必须远小于负载电阻变换到初级侧后的值\(D^{'2}R\)。这在较低的占空比时容易实现，也就是\(D^{'}\)接近于1比接近于0更容易实现。从图3.15可以看到，低占空比时，效率较高，但在\(D=1\)附近迅速下降到0。

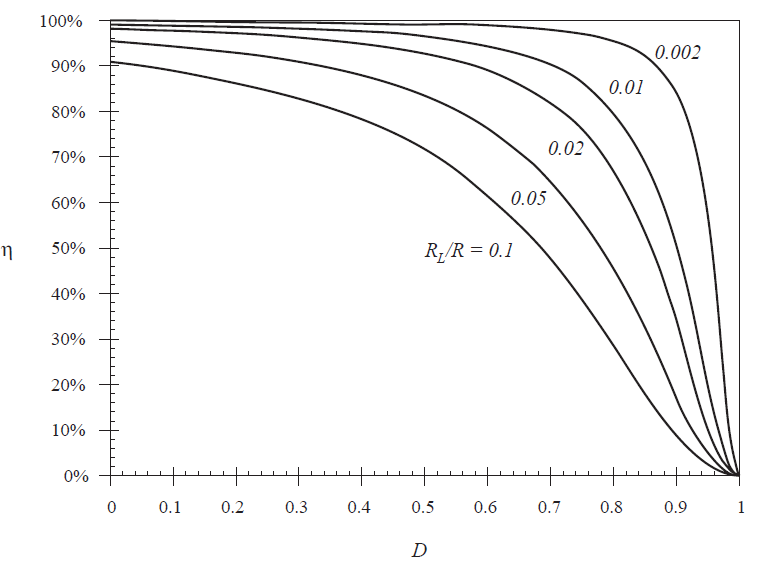
Fig 3.15 Efficiency, for various values of \(R_{L}\)

因此，可以通过考虑其他例如电感铜损对基本的直流变压器模型进行完善。这个模型描述了变换器的基本特性，包括：(a)直流电压和电流的变换;(b)功率损耗的二次效应;(c)变换比\(M\)。通过求解模型，不仅可以得到输出电压\(V\)，同时可以得到电感电流\(I\)以及效率\(\eta\)。可以使用所有已知的电路分析技术来求解模型，从而使其成为一种功能强大且用途广泛的分析方法。

到目前为止，所考虑的是一个相对简单的实例，其中只有一个损耗元素\(R_{L}\)。当然，实际的变换器要复杂的多，并且包含大量损耗因素。当要解决复杂电路求解输出电压和效率时，工程师应该选择最简单，最有意义的方法。编写大量并列循环和节点方程并不是最佳方法，因为其结果可能是几页代数值。并且，工程师通常会在这个过程中出现代数错误。实践的工程师经常在找到正确答案之前就放弃了。等效电路的方法避免了这种情况，因为可以通过众所周知的电路变换(例如将电路元件变换到变压器次级侧)来简化电路。通常可以使用分压公式及其他公式来检查答案。工程师会对结果的正确性充满信心。