[Fundamental of Power Electronics]-PART I-3.稳态等效电路建模，损耗和效率-3.1 直流变压器模型

3.1 直流变压器模型

如图3.1所示，任何开关变换器都包含三个部分：功率输入，功率输出以及控制输入。输入功率按控制输入进行特定的功率变换输出到负载。理想情况下，这些功能将以100%的效率完成，因此

\[P_{in} = P_{out} \tag{3.1} \]

或者

\[V_{g} I_{g} =VI \tag{3.2} \]

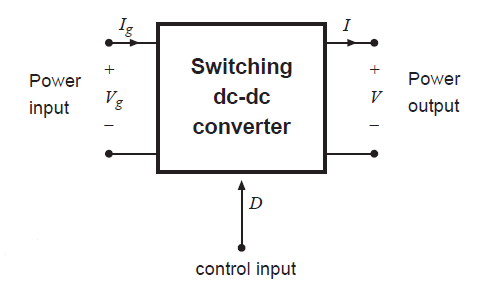
Fig 3.1 Basic equations of an ideal DC-DC converter

这些关系只有在平衡（DC）条件下才是成立的：在瞬态过程，变换器中的电感以及电容在电路中存储的能量可能会改变，导致违背式(3.1)及(3.2)。

在前面的章节，我们发现可以用以下形式的方程来表达变换器的输出电压：

\[V= M(D)V_{g} \tag{3.3} \]

其中\(M(D)\)为变换器的稳态变换比。例如，Buck变换器的\(M(D)=D\)，Boost变换器的\(M(D)=1/(1-D)\)。通常情况下，对于在连续导通模式下运行并包含相等数量的独立电感器和电容器的理想PWM变换器，可以证明平衡变换比\(M\)是\(D\)的函数，并且与负载无关。

将式(3.3)代入(3.2)得到

\[I_{g} = M(D) I \tag{3.4} \]

因此，变换器的端口电流以相同的变换比联系起来了。

式(3.3)与(3.4)表明，变换器可以用图3.2所示的受控源进行建模。通过对类似理想变压器的式(3.1)到(3.4)的实现，获得了一个等效的但更加有物理含义的模型(图3.3)。在理想变压器中，如等式(3.1)(3.2)描述的相同，输入功率与输出功率相同。同样输出电压等于匝数乘以输入电压，其中的匝数为平衡变换比\(M(D)\)，与式(3.3)一致。最后，输入电流与输出电流以式(3.4)的匝数比关系进行关联。

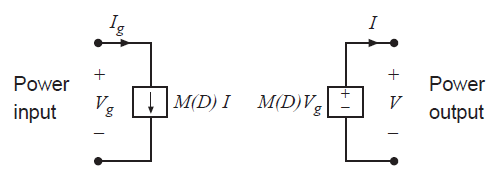
Fig 3.2 dependent sources

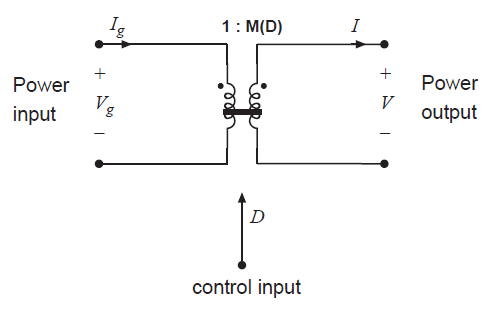
Fig 3.3 DC Transformer

因此，我们可以使用图3.3所示的理想直流变压器模型对理想的DC-DC变换器进行建模。这个模型表示了任何开关DC-DC变换器的一阶直流特性：理想情况下以占空比\(D\)控制的100%效率的直流电压和电流的变换。水平的实线表示该元件是理想的，并且能够传递直流电压和电流。尽管标准的磁芯变压器不能变换直流信号(施加直流电压后会饱和)，但是我们仍然可以自由定义图3.3的理想模型，来对DC-DC变换器进行建模。实际上，没有物理直流变压器就是构建DC-DC变换器的原因之一。因此，可以使用图3.3的等效电路对图3.1的DC-DC变换器进行建模。这种等效电路的一个优点是，对于固定的占空比，它是时不变的：没有开关或开关纹波需要处理，并且仅对波形重要的直流分量进行建模。

变换与简化含变压器电路的规则同样适用于包含DC-DC变换器的电路。例如，考虑图3.4的电路，其中电阻负载连接到变换器的输出，电源通过戴维南等效建模为电压源\(V_{1}\)与电阻\(R_{1}\)。然后1中的变换器被2中的变压器模型替代。然后将\(V_{1}\)和\(R_{1}\)与直流变压器合并：直流电压源\(V_{1}\)乘以变换比\(M(D)\)，电阻\(R_{1}\)乘以\({M(D)}^2\)。现在就可以采用分压方程来求解输出电压。

\[V = M(D)V_{1} \frac{R}{R+M(D)^2 R_{1}} \tag{3.5} \]

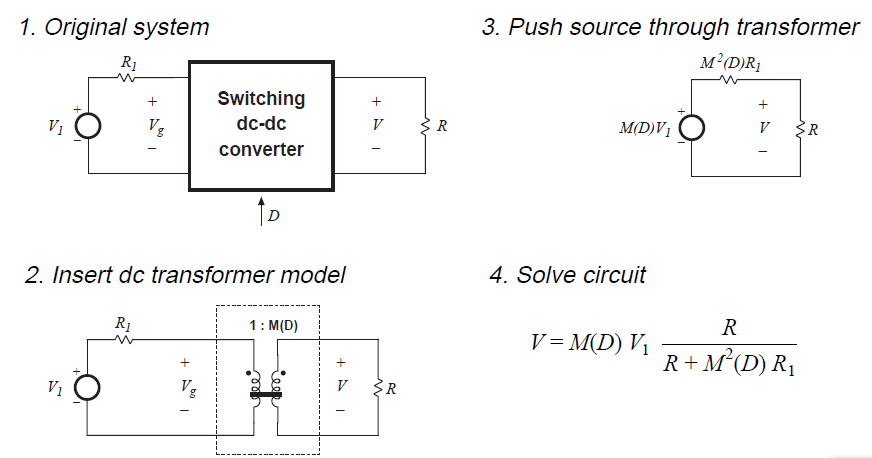
Fig 3.4 Use of the dc transformer model

显然，直流变压器等效电路/方法是理解包含变换器电路的有力工具。