[Fundamental of Power Electronics]-PART I-2.稳态变换器原理分析-2.3 Boost 变换器实例

2.3 Boost 变换器实例

图2.13(a)所示的Boost变换器器是另一个众所周知的开关模式变换器，其能够产生幅值大于直流输入电压的直流输出电压。图2.13(b)给出了使用MOSFET和二极管的开关的实际实现。让我们应用小纹波近似以及电感伏秒平衡和电容电荷平衡的原理来找到该变换器的稳态输出电压和电感电流。

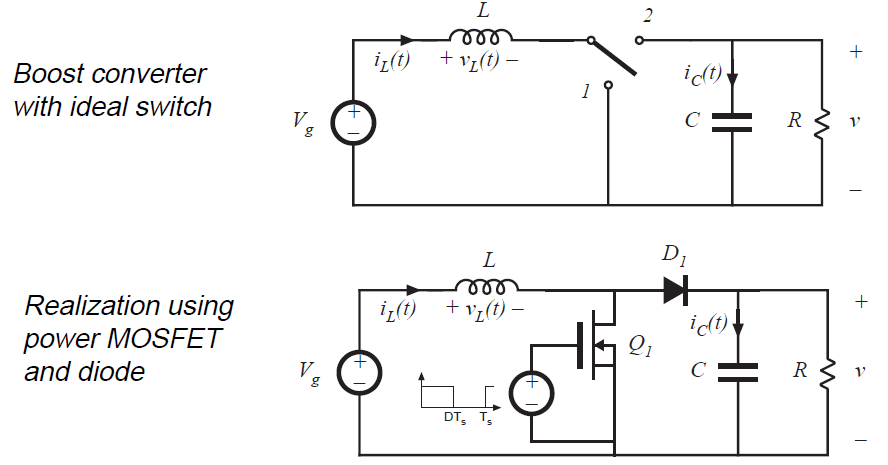
Fig 2.13 Boost converter example

将开关置于位置1时，电感器的右侧接地，从而形成图2.14(a)的电路。此子间隔的电感电压和电容电流为：

$$v_{L}=V_{g} \\ i_{C}=-\frac{v}{R} \tag{2.28}$$

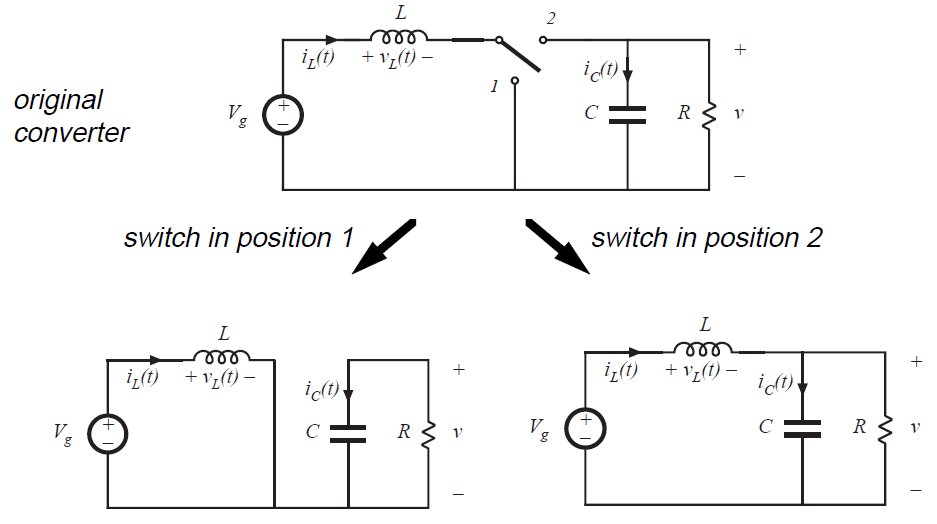
Fig 2.14 Boost converter circuit

使用线性小纹波近似，令$v \approx {V}$，得到

$$v_{L}=V_{g} \\ i_{C}=-\frac{V}{R} \tag{2.29}$$

在开关处于位置2的情况下，电感连接至输出，从而得到图2.14(b)的电路。然后，电感电压和电容电流为：

$$v_{L}=V_{g}-v \\ i_{C}=i_{L}-\frac{V}{R} \tag{2.30}$$

利用小纹波近似，即$v \approx V$，$i_{L} \approx I$，得到：

$$v_{L}=V_{g}-V \\ i_{C}=I-\frac{V}{R} \tag{2.31}$$

根据公式(2.29)和(2.31)绘制出电感电压和电容电流波形如图2.15所示：

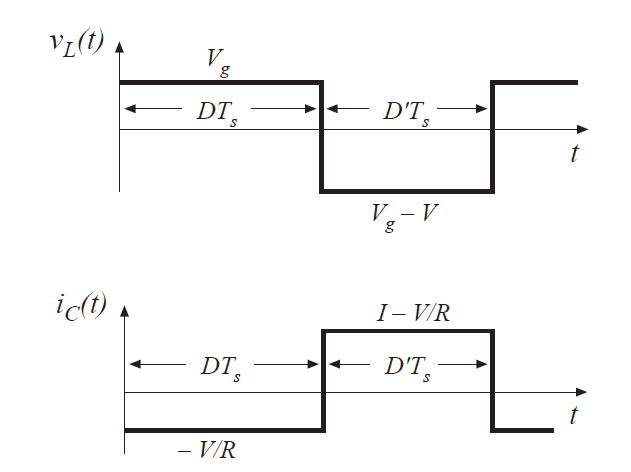
Fig 2.15 Inductor voltage and capacitor current waveforms

从图2.15(a)的电感电压波形可以推断出直流输出电压V大于输入电压$V_{g}$。在第一个子间隔内，直流输出电压V等于直流输入电压$V_{g}$，并且正的伏秒被施加到电感器。因为在稳态下，在一个开关周期内施加的总伏秒必须为零，所以在第二个子间隔内必须施加负伏秒。所以，第二个子间隔内的电感电压$V_{g}-V$必须为负。因此，输出电压V大于直流输入电压$V_{g}$。

在一个开关周期内施加到电感器的总伏秒数为：

$$\int_0^{T_{s}} v_{L}(t)dt =V_{g} D T_{s}+(V_{g}-V) D^{'} T_{s} \tag{2.32}$$

令上式为0，并且整理得到：

$$V_{g} (D+D^{'})-V D^{'}=0 \tag{2.33}$$

求解上式中的V，同时有$(D+D^{'})=1$,得到输出电压为：

$$V=\frac{V_{g}}{D^{'}} \tag{2.34}$$

电压转换比M(D)是DC-DC变换器的输出与输入电压之比。根据公式(2.34)可得出电压转换比为：

$$M(D)= \frac{V}{V_{g}} = \frac{1}{D^{'}}= \frac{1}{1-D} \tag{2.35}$$

该方程式描绘如图2.16所示。在D=0，$V=V_{g}$时，输出电压随D的增加而增加，在理想情况下，随着D的趋向于1趋于无穷大。因此，理想的升压变换器能够产生任何大于输入电压的输出电压。当然，实际的升压变换器会产生对输出电压的限制。在下一章中，对组件的非理想特性进行了建模，发现实际的升压转换器的最大输出电压确实受到限制。但是，如果非理想度足够小，则可以产生非常大的输出电压。

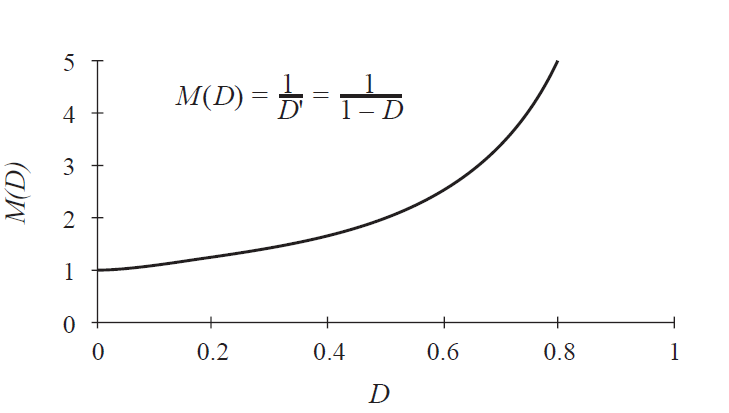
Fig 2.16 Conversion ratio M(D) of the boost converter

电感电流的直流分量是通过使用电容电荷平衡原理得出的。在第一个子间隔期间，电容提供负载电流，并且电容部分放电。在第二个子间隔期间，电感电流为负载供电，此外还为电容充电。通过积分图2.15(b)的波形，可以得出一个开关周期内电容器电荷的净变化:

$$\int_0^{T_{s}} i_{C}(t)dt =- \frac{V}{R} D T_{s}+(I- \frac{V}{R}) D^{'} T_{s} \tag{2.36}$$

令上式为0，整理可得：

$$-\frac{V}{R} (D+D^{'})+ ID^{'} =0 \tag{2.37}$$

根据上式，求解出电流为：

$$I = \frac{V}{D^{'}R} \tag{2.38}$$

根据上式得到电感电流直流分量I，代入式(2.34)消除输出电压V可得：

$$I = \frac{V_{g}}{{D^{'}}^{2} R} \tag{2.39}$$

该方程式如图2.17所示。可以看出，电感电流随着D接近1而变大。

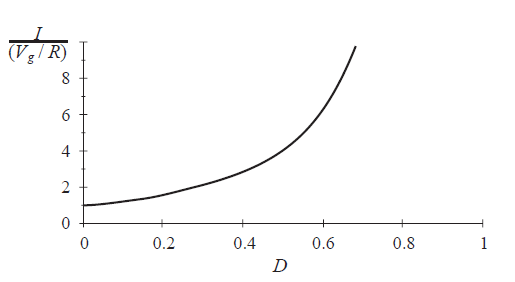
Fig 2.17 Variation of inductor current dc component I with duty cycle,boost converter

该电感电流与升压变换器中的直流输入电流一致，大于负载电流。从物理上讲，必须是这样：在理想的变换器元件情况下，变换器的输入和输出功率相等。由于变换器的输出电压大于输入电压，因此输入电流必须同样大于输出电流。实际上，电感电流流过半导体正向压降，电感绕组电阻和其他功率损耗源，当占空比接近1时，电感电流将变得非常大，并且这些组件的非理想性会导致较大的功率损耗。所以，升压变换器的效率在高占空比时迅速降低。

接下来，让我们绘制电感电流$i_{L}(t)$波形并推导电感电流纹波的表达式。图2.15已经给出了电感电压波形，因此我们可以直接绘制电感电流波形。在第一个子间隔期间，将开关置于位置1，电感电流的斜率由下式给出：

$$\frac {di_{L}(t)}{dt}= \frac{v_{L}(t)}{L} = \frac{V_{g}}{L} \tag{2.40}$$

同样，当开关位于位置2时，电感器电流波形的斜率为:

$$\frac {di_{L}(t)}{dt}= \frac{v_{L}(t)}{L} = \frac{V_{g}-V }{L} \tag{2.41}$$

电感电流波形如图2.18所示。在第一个子间隔期间，电感电流的变化等于斜率乘以子间隔的长度，或者：

$$2 \Delta i_{L} = \frac{V_{g}}{L} D T_{s} \tag{2.42}$$

求解$\Delta i_{L}$，得到

$$\Delta i_{L} = \frac{V_{g}}{2L} D T_{s} \tag{2.43}$$

该表达式可以用于给定电流纹波值后选择相应的电感值。

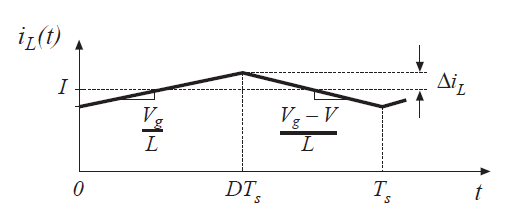
Fig 2.18 Boost converter inductor current waveform

同样，可以画出电容电压$v(t)$波形，并为输出电压纹波大小$\Delta v$导出一个表达式。电容电流$i_{C}(t)$波形如图2.15所示。在第一个子间隔内，电容电压$v(t)$波形的斜率为:

$$\frac {dv_{C }(t)}{dt}= \frac{i_{C}(t)}{C} = \frac{-V }{RC} \tag{2.44}$$

第二个时间间隔内：

$$\frac {dv_{C }(t)}{dt}= \frac{i_{C}(t)}{C} = \frac{I}{C}- \frac{-V }{RC} \tag{2.45}$$

电容电压波形如图2.19所示。在第一个子间隔期间，电容电压的变化等于斜率乘以子间隔的长度：

$$-2 \Delta v= - \frac{V}{RC} DT_{s} \tag{2.46}$$

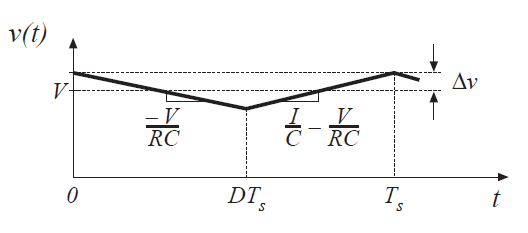
Fig 2.19 Boost converter output voltage waveform

求解$\Delta v$ ，得到：

$$\Delta v= \frac{V}{2RC} DT_{s} \tag{2.47}$$

该表达式可用于选择电容器值C以获得给定的输出电压纹波大小。