连续函数离散化-以SOGI为例

0. 引言

0.1 本文内容

基于SOGI函数，将s域传递函数转换为离散的z域函数，并以m语言形式进行实现，在simulink中封装为m-function并进行验证

0.2 学到什么

离散化方法
函数程序实现方法

1. SOGI简介

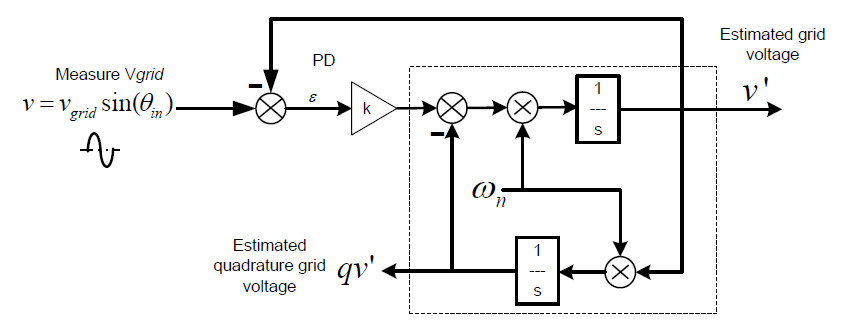
以TI官方文档中单相锁相环中SOGI应用为例

框图如下所示

正弦信号经过SOGI可得到同相信号及正交信号

2. 传递函数

同相传递函数

\[H_{d}(s)=\frac{v^{\prime}}{v}(s)=\frac{k \omega_{n} s}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{1} \]

正交信号传递函数为

\[H_{q}(s)=\frac{q v^{\prime}}{v}(s)=\frac{k \omega_{n} ^2}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{2} \]

3. 离散化

采用双线性变换将s域函数离散至Z域

3.1 手动离散

双线性变换公式为

\[s=\frac{2}{T_{s}}\frac{z-1}{z+1} \tag{3} \]

将式3代入式1得到

\[H_{d}(z)=\frac{k \omega_{n} \frac{2}{T_{s}}\frac{z-1}{z+1}}{(\frac{2}{T_{s}}\frac{z-1}{z+1})^{2}+k \omega_{n} (\frac{2}{T_{s}}\frac{z-1}{z+1})+\omega_{n}^{2}} \tag{4} \]

这里使用以下两个替换

\[x=2k\omega_{n}T_{s} \tag{5} \]

\[y=( \omega_{n} T_{s})^2 \tag{6} \]

得到

\[H_{d}(z)=\frac{\left(\frac{x}{x+y+4}\right)+\left(\frac{-x}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{b_{0}+b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{7} \]

同理得到正交函数的离散形式

\[H_{q}(z)=\frac{\left(\frac{k \cdot y}{x+y+4}\right)+2\left(\frac{k \cdot y}{x+y+4}\right) z^{-1}+\left(\frac{k \cdot y}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{q b_{0}+q b_{1} z^{-1}+q b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{8} \]

3.2 基于MATLAB的离散方法

看完上面的离散过程，很明显，太麻烦，有没有简单点的方法呢？哎，还真有，MATLAB只需要一条命令就能搞定
MATLAB中c2d命令可通过多种离散方法将连续函数离散化，这里为保持一致，同样以双线性变换（tustin）为例进行介绍
(了解更多c2d命令，请点击了解详情)
具体用法如下

sysd = c2d(sys,Ts,'method')

其中，sys与sysd分别为离散前后函数，Ts为采样周期，method为离散化方式，这里就是tustin

直接给出离散过程的MATLAB代码

%%定义s为传递函数
s = tf('s');    

%%定义各参数
k = 0.5;
Wn = 100*pi;    %%50Hz
Ts = 1e-4;          %%10kHz

%%写出传递函数
Hd_s = k*Wn*s/(s^2+k*Wn*s+Wn^2);
Hq_s = k*Wn^2/(s^2+k*Wn*s+Wn^2);

Hd_z = c2d(Hd_s,Ts,'tustin')
Hq_z = c2d(Hq_s,Ts,'tustin')

运行结果为

Hd_z =
 
  0.007791 z^2 - 0.007791
  -----------------------
  z^2 - 1.983 z + 0.9844
 
Sample time: 0.0001 seconds
Discrete-time transfer function.


Hq_z =
 
  0.0001224 z^2 + 0.0002448 z + 0.0001224
  ---------------------------------------
          z^2 - 1.983 z + 0.9844
 
Sample time: 0.0001 seconds
Discrete-time transfer function.

3.3 对比

上面已经给出了采用MATLAB进行离散的结果，采用同样的参数，这里基于式5-8，给出传统计算方式的结果

Parameter	value	Parameter	value
b0	0.0078	qb0	0.00012238
b1	0	qb1	0.00024476
b2	-0.0078	qb2	0.00012238
a1	1.9834	a2	-0.9844

可能会看到，这里系数正负号与MATLAB计算出结果有所不同，这里实际结果没错哈，认为错了的自己好好检查！

4.SOGI的程序实现

既然已经得到离散的SOGI函数，如何将其写成程序呢，这里以MATLAB语言为例，C语言同理

4.1 离散序列的获得

根据式7和8，我们知道

\[\frac{U_{o}(z)}{U_{i}(z)}=\frac{b_{0}+b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{9} \]

\[\frac{U_{qo}(z)}{U_{i}(z)}==\frac{q b_{0}+q b_{1} z^{-1}+q b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{10} \]

容易写成序列方程

\[\ U_{o} (k)-a_{1}U_{o} (k-1)-a_{2}U_{o} (k-2)=b_{0}U_{i}(k)+b_{2}U_{i}(k-2) \tag{11} \]

\[\ U_{qo} (k)-a_{1}U_{qo} (k-1)-a_{2}U_{qo} (k-2)=qb_{0}U_{i}(k)+qb_{1}U_{i}(k-1)+qb_{2}U_{i}(k-2) \tag{12} \]

4.2 封装一个m-function

根据上面的式子我们很容易可以写出相应的程序，但为了在simulink中验证程序的正确性，我们在这里把SOGI封装为一个m-function块以便使用
不了解Matlab的function块功能的自行百度

很容易知道，对于一个完整的SOGI函数，有一个输入端，两个输出端。函数中各参数均设定为外部给定
下面直接给出相应程序

%%
%%函数声明
function [uo,quo]   = Orthogonal_Generator(ui,Ts,w,k)

%%
%%定义各中间变量
persistent x;
persistent y;
persistent temp;
persistent b0;
persistent b2;
persistent a1;
persistent a2;
persistent qb0;
persistent qb1;
persistent qb2;
persistent u0;          %%代表ui(k)
persistent u1;          %%代表ui(k-1)
persistent u2;          %%代表ui(k-2)
persistent osg_u0;  %%代表uo(k)
persistent osg_u1;  %%代表uo(k-1)
persistent osg_u2;  %%代表uo(k-2)
persistent osg_qu0; %%代表uqo(k)
persistent osg_qu1; %%代表uqo(k-1)
persistent osg_qu2; %%代表uqo(k-2)

%%
%%初始化各中间变量
if isempty(x)     x= 0; 
end
if isempty(y)     y= 0; 
end
if isempty(temp)  temp= 0; 
end
if isempty(b0)    b0= 0; 
end
if isempty(b2)    b2= 0; 
end
if isempty(a1)    a1= 0; 
end
if isempty(a2)    a2= 0; 
end
if isempty(qb0)   qb0= 0; 
end
if isempty(qb1)   qb1= 0; 
end
if isempty(qb2)   qb2= 0; 
end
if isempty(u0)    u0= 0; 
end
if isempty(u1)    u1= 0; 
end
if isempty(u2)    u2= 0; 
end
if isempty(osg_u0)   osg_u0= 0; 
end
if isempty(osg_u1)   osg_u1= 0; 
end
if isempty(osg_u2)   osg_u2= 0; 
end
if isempty(osg_qu0)   osg_qu0= 0; 
end
if isempty(osg_qu1)   osg_qu1= 0; 
end
if isempty(osg_qu2)   osg_qu2= 0; 
end

%%
%%各系数赋值
x      = 2*k*w*Ts;
y      = w*Ts*w*Ts;
temp   = 1/(x+y+4.0);
b0     = x*temp;
b2     = (-1.0)*b0;
a1     = (2.0)*(4.0-y)*temp;
a2     = (x-y-4)*temp;
qb0    = (k*y)*temp;
qb1    = qb0*(2.0);
qb2    = qb0;

%%
%%计算过程，对应式11离散序列
u0            = ui;
osg_u0        = (b0*(u0-u2)) + (a1*osg_u1) + (a2*osg_u2);
osg_u2        = osg_u1;
osg_u1        = osg_u0;
%%对应式12离散序列
osg_qu0       = (qb0*u0) + (qb1*u1) + (qb2*u2) + (a1*osg_qu1) + (a2*osg_qu2);
osg_qu2       = osg_qu1;
osg_qu1       = osg_qu0;
%%更新序列值
u2            = u1;
u1            = u0;
%%输出
uo            =osg_u0;
quo           =osg_qu0;

程序有了，我们在simulink中的Library中找到MATLAB Function，写入上面函数即可

为了进行测试，我们给定一个幅值100，频率50Hz的正弦信号，其余与上文相同，整个测试模型如下图所示

同时，要想模型按离散进行仿真，还需要进行相应设置如下图所示，关键在于固定步长

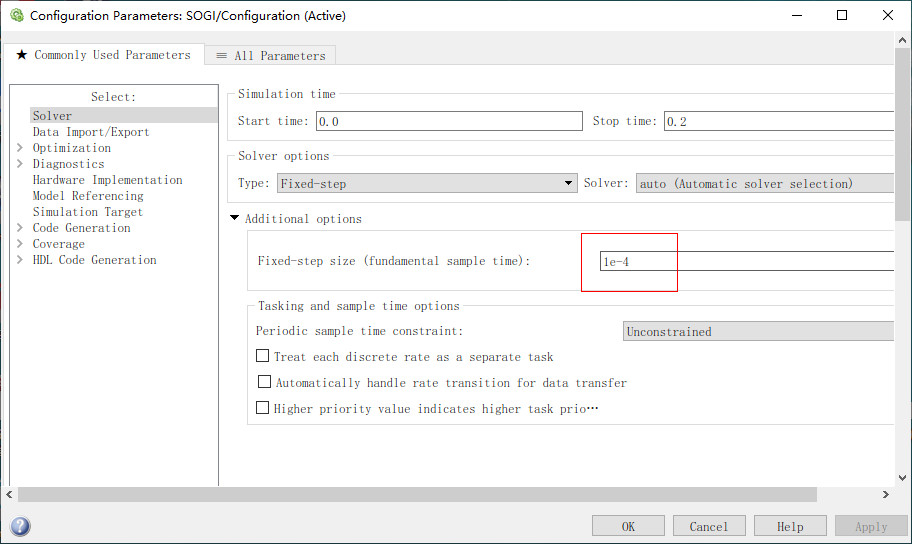
至此，程序编写及模型搭建，环境搭建就已经完成

4.3 测试

这里运行simulink仿真，将输入信号，输出同相信号与输出正交信号进行对比，如下图所示

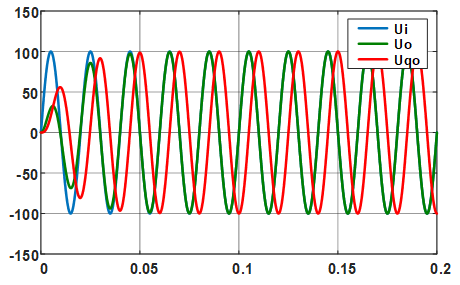
很显然，在经过两个周期后，同相输出信号与输入重叠，正交信号相差为90°，测试结果表明程序及模型的正确性