算法 递归与回溯

递归

递归是利用方法栈帧后进先出的特点。先进入的方法栈帧等待后进入的方法栈帧计算结果。例如:f(n)=f(n-1)+1，f(n)等待f(n-1)的结果，依次递归向下优先算出最低层结果后，再依次返回根据下层结果计算。

递：一层一层深入(依次执行前置代码)，直到到达递归终止条件(一定要有终止条件，不再执行自己)。

等待下层方法栈帧执行完成/return结果......

归：再从底层一层一层返回(依次执行后置代码)。利用JAVA方法栈帧局部变量独立的特性，保证退回栈帧时状态为原始状态。

递归也是循环的一种表现，不过比循环更容易执行多层回退、前序后序操作。但是递归因为要重复的创建栈帧所以效率没有循环高。

递归思想，开发人员只要把设计重心放到设计一步操作的统一模板即可，包含进入到这一步执行的代码，是否可以进入下一步，返回当前步骤后继续执行的代码。

循环代替

一般循环也可以用while循环执行回退，但是比较麻烦。需要借助一个Stack数据结构保存各步状态，并且手动递增和回退，并保证正确性。

 

常涉及的算法思想

分治思想：

快速排序：典型的递归前置思想，先执行取中分边，再左右向下递归

归并排序：典型的递归后置思想，先取中左右向下递归，再从最底层一层层向上执行归并。

回溯思想：

DFS，斐波那契.....等等

 

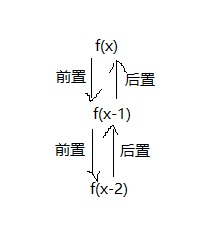
2 复用避免重复计算

   可以适当配和动态规划思想，递归时可以把各步结果保存，可以复用。 斐波那契数列就是典型例子

3  斐波那契数

//递归方式实现斐波那契数
	public static long rec_fib(long i) {
		long result = 0;
		if(i <= 0) return 0; //递归终止
		
		if(i == 1 || i == 2) //递归终止
			result = 1;
		else {
                        System.out.println("递归前置");
			result = rec_fib(i-1)  //返回继续 <=======> 进入下层
                                + rec_fib(i-2);  //返回继续 <=======> 进入下层
                        System.out.println("递归后置");
		}
		return result;
	}

回溯算法

回溯算法很符合人类思维逻辑，适用范围非常广泛。

回溯算法是一种试探性算法，也是穷举法，利用DFS的解决思路，把整个问题想成一个树形/图形节点关系，不同的可能代表不同节点分支。从一个节点开始以DFS一步一步向下试探，不满足条件/目标则退回上一步节点探性其他分支，若没有剩余分支再退回上一步。其也是递归特性的一种经典表现。

明确终止向下试探的边际条件， 设计递归前置代码处理准备进入下一步之前的工作，递归后置代码处理再次退回当前节点时当前节点需要继续执行的工作。

典型问题：leetcode39、78

给定一组不含重复元素的整数数组 nums={0,1,2}，返回该数组所有可能的子集（幂集）。

按照代码执行顺序：

[]，[0]，[0,1]，[0,1,2]，[0,2]，[1]， [1,2]，[2]

第一层循环：确定子集首位，当遇到第一个选项分支时直接递归进入第二层；

第二层循环：确定第二位 ......以此类推，没有可/未选分支了，再退回上一位，找其他分支。

 public static void main(String[] args) {
        int[] nums = {0,1,2};
        System.out.println(subsets(nums));
    }
 
    public static List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList();//结果集（所有子集）
        List<Integer> temp = new ArrayList();//记录到当前节点的路过节点（当前路径）
 
        dfs(result,temp,nums,0);
 
        return result;
    }
 
    public static void dfs(List<List<Integer>> result, List<Integer> temp, int nums[], int index){
 
        result.add(new ArrayList<Integer>(temp));//temp添加到结果集中
 
        //从index位置向后
        for (int i = index; i < nums.length; i++) {
            //添加第i个数进入temp中
            temp.add(nums[i]);
            //进入到下一层，将temp添加到结果集中并添加下一个数
            dfs(result,temp,nums,i+1); //返回继续 <=======> 进入下层
            //从下层返回后，把最新添加的一个数删掉继续循环（temp手动回退到本层原状态）
            temp.remove(temp.size()-1);
        }//循环完返回上一层递归
 
    }