排序算法 - 堆排序
排序算法 - 堆排序
曾经也是对堆排序望而却步,但是人总是要学一些自己不会的东西,不然还有什么乐趣。Getting out of your comfort zone!!
下面就按照什么是二叉堆 --> 如何进行堆排序 --> 堆排序时间/空间复杂度多少进行行文介绍:
1. 什么是二叉堆?
二叉树结构大家都很熟悉,满二叉树结构是基于二叉树引出的一种结构,满二叉树的每一层的节点数都达到最大,也即深度为k的满二叉树节点数为2^(k+1) - 1个(2 ^ 0 + 2 ^ 1 + 2 ^ 2 + .. + 2 ^ k)。
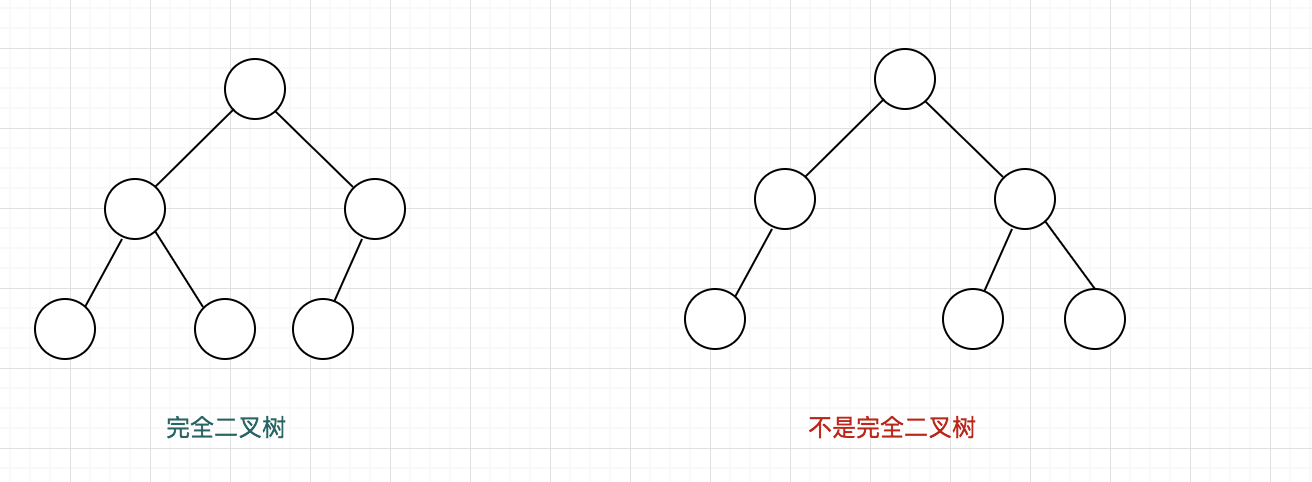
基于满二叉树结构引出另一种结构:完全二叉树。完全二叉树的特征:
- a. 除了最后一层,其余各层就是一颗满二叉树
- b. 最后一层可以不含有最大个数的节点,但是节点都位于左边
![]()
满足以下两个特点的二叉树就是一个二叉堆:
- 特征1:是一颗完全二叉树
- 特征2:每个节点都是其对应子节点中的最大值或是最小值
如果是最大值时,该堆则为最大堆;如果是最小值时,该堆则为最小堆。

2. 如何实现堆排序?
以升序为例(),如果一个数组是最大堆,堆顶就是该数组中的最大值。如果将堆顶元素与数组中的最后一个元素对换,将除了最后一个元素的调整成一个新的最大堆,在重复以上操作,然后整个数组就变成升序。这样就达到升序排序的目的。所以先要将该数组调整成对结构。
2.1 数组调整成最大堆
用数组如何表示完全二叉树:数组中第一个节点(索引为0)为堆顶,那么其左子树节点索引为1,其右子树节点索引为2,依次类推,索引为i的节点,其左子树节点索引为2*i+1, 右子树节点索引为2*i+2。但是如果计算出的索引超过了数组的最大索引下标,这个节点就为叶子节点。

要将一个完全二叉树调整成二叉堆结构,其叶子节点已经满足二叉堆的特征2,剩下就只需依次调整其非叶子节点以满足堆的特征。
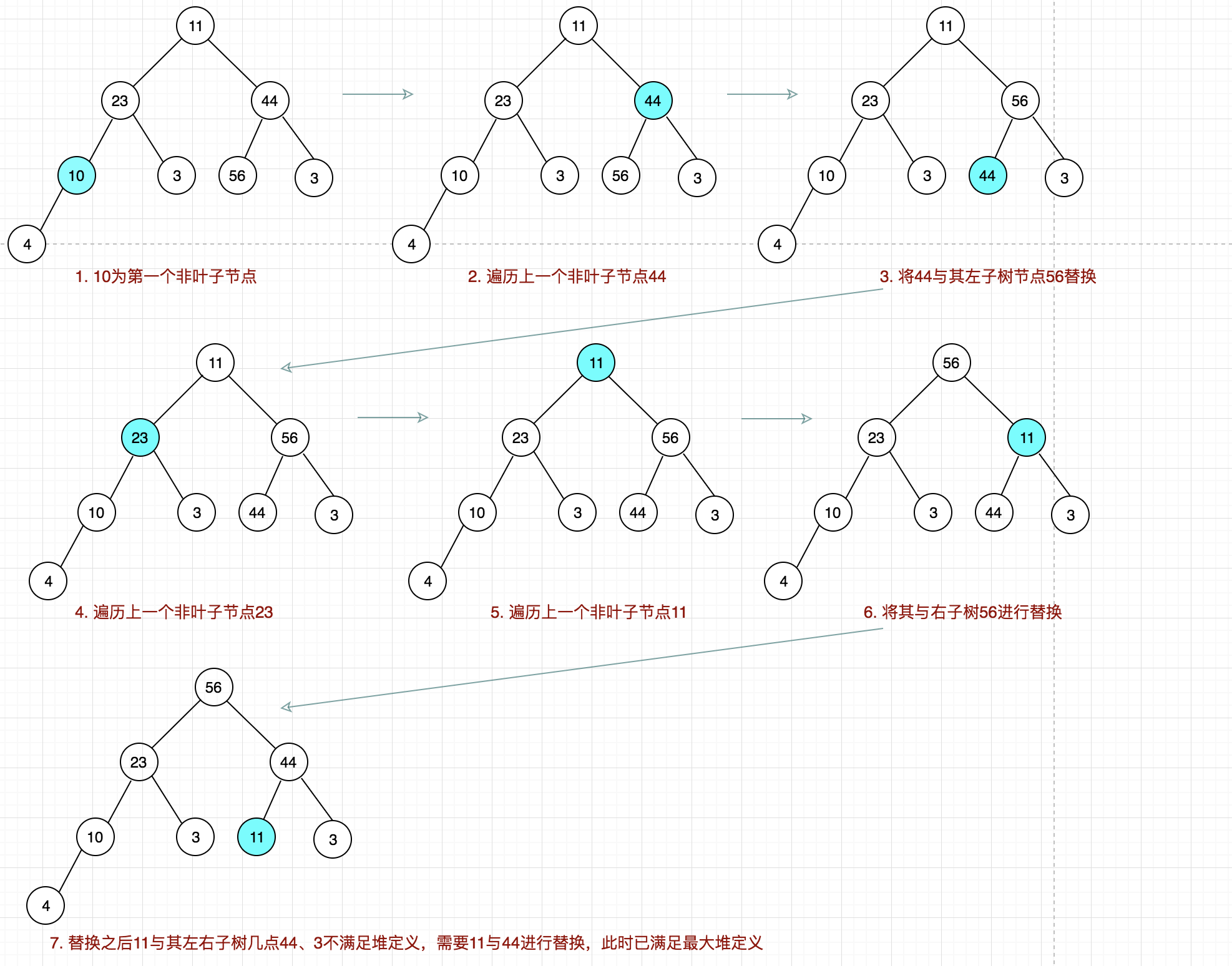
步骤如下:
- I. 找出最后一个非叶子节点
- II. 比较它与其两个左右子树节点大小
- II.1 如果左右子树中最大值大于该节点
- II.1.1 将其进行替换
- II.1.2 同时判断被替换子节点是否有孩子节点,如有的话则需要判断是否满足堆的定义,不满足的话需要做调整。
- II.1 如果左右子树中最大值大于该节点
- III. 然后依次调整上一个非叶子节点,直到根节点。
![调整成堆结构]()
上代码
/**
* 构建最大二叉堆
* @param arr
*/
private void build(int arr[]) {
if(arr == null || arr.length <= 0) {
return;
}
// 获取最后一个非叶子节点下标
int lastNonLeafIndex = this.getLastNonLeafIndex(arr.length);
// 遍历非叶子节点做调整
for(int index = lastNonLeafIndex; index >= 0; index--) {
// 去最大的子树节点下标
int maxChild = index*2 + 1;
if(index*2 + 2 < arr.length && arr[index*2 + 2] > arr[index*2+1]) {
maxChild = index*2 + 2;
}
if(arr[maxChild] > arr[index]) {
// 替换节点与子节点的值
int tmp = arr[index];
arr[index] = arr[maxChild];
arr[maxChild] = tmp;
// 判断是否有子节点
if(maxChild < lastNonLeafIndex) {
// 该子节点有孩子节点
this.adjust(arr, maxChild, arr.length);
}
}
}
}
/**
* 基于节点调整它与其子节点的大小顺序
* @param arr
* @param index
* @param length - 有效长度
*/
private void adjust(int[] arr, int index, int length) {
while(index < length) {
int maxChild = index * 2 + 1;
if(maxChild >= length) {
// 该节点没有子节点,退出
break;
}
// 找出该节点两个(可能只有一个左孩子)子节点中的最大值节点下标
if(index * 2 + 2 < length && arr[index * 2 + 2] > arr[index * 2+1]) {
maxChild = index * 2 + 2;
}
if(arr[maxChild] <= arr[index]) {
// 子节点已经不大于该节点数值,退出
break;
}
// 子节点已经大于该节点数值,替换
int tmp = arr[index];
arr[index] = arr[maxChild];
arr[maxChild] = tmp;
// 将替换的子节点下标坐下一次操作的目标
index = maxChild;
}
}
/**
* 获取堆结构中最后一个非叶子节点下标
* @param length
* @return
*/
private int getLastNonLeafIndex(int length) {
if((length & 1) == 1) {
// 节点数目为奇数时,最后一个非叶子节点有右子树(2*i + 2 = arr.length - 1)
return (length - 3) / 2;
} else {
// 节点数目为偶数时,最后一个非叶子节点只有左子树(2*i + 1 = arr.length - 1)
return (length - 2) / 2;
}
}
验证:
public static void main(String[] args) {
int[] arr = new int[] {11, 23, 44, 10, 3, 56, 3, 4};
System.out.println("Before: " + Arrays.toString(arr));
new HeapSort().build(arr);
System.err.println("After adjusting: " + Arrays.toString(arr));
}
// 输出结果
Before: [11, 23, 44, 10, 3, 56, 3, 4]
After adjusting: [56, 23, 44, 10, 3, 11, 3, 4]
2.2 排序操作
基于上述的2.1操作之后,原始的数组已经是一个堆结构了,后续只要将堆顶元素依次与数组中的最后一个有效元素进行替换即可。
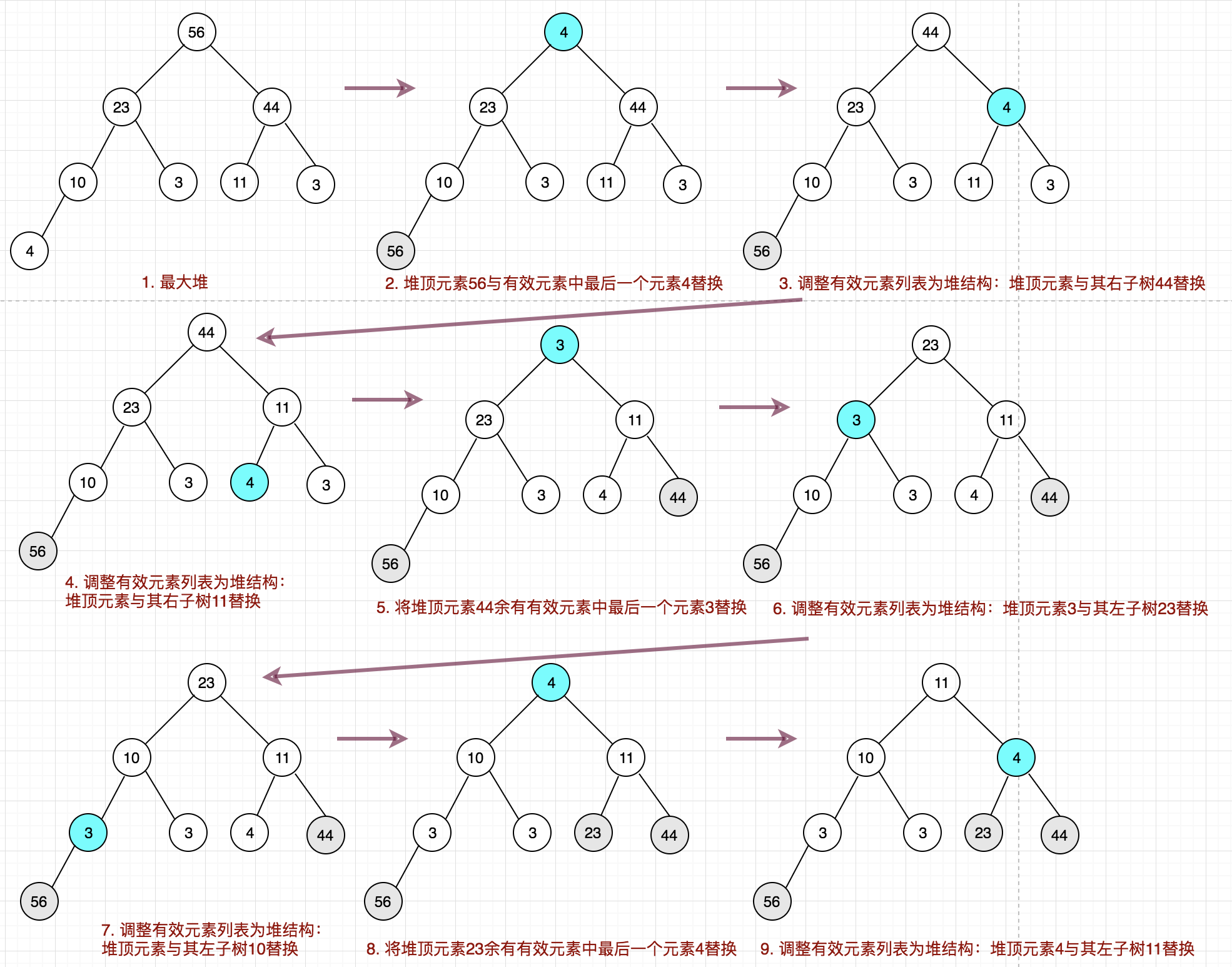
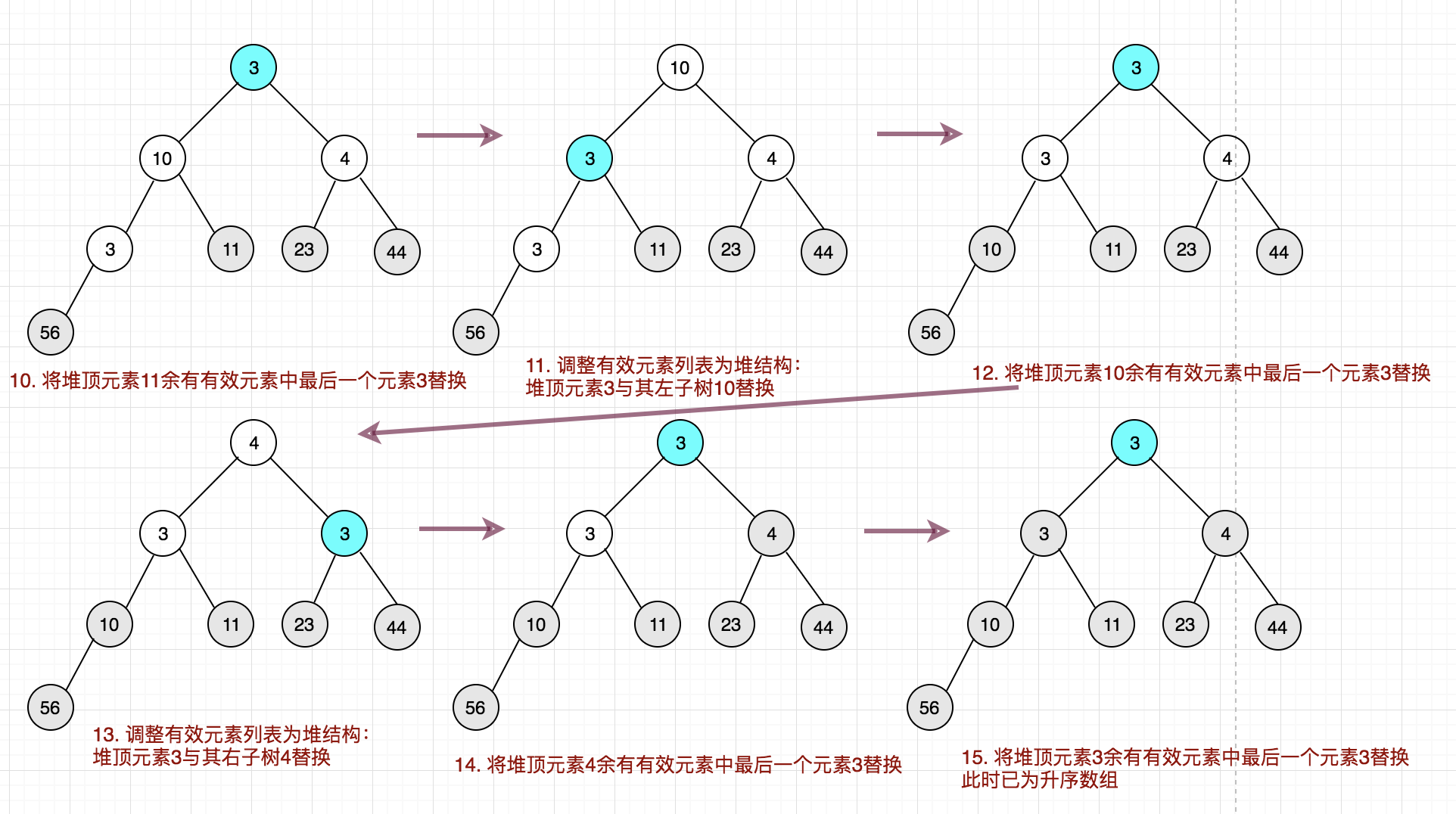
上代码:
/**
* 排序操作
* @param arr
*/
public void sort(int[] arr) {
if(arr == null || arr.length <= 0) {
return;
}
// 构建堆 - 将原数组调整成最大堆
this.build(arr);
// 排序
// i初始值为原始数组最后一个下标,
// 进行一次操作之后,数组中有效的最后一个元素下标即为i-1, 如此依次操作
for (int i = arr.length - 1 ;i > 0; i--) {
// 将堆顶元素与数组中有效的最后一个元素进行替换
int tmp = arr[i];
arr[i] = arr[0];
arr[0] = tmp;
// 替换之后前面有效的数组已经不是一个最大堆,需要进行调整
// 此时有效长度就是i
this.adjust(arr, 0, i);
}
}
验证:
public static void main(String[] args) {
int[] arr = new int[] {11, 23, 44, 10, 3, 56, 3, 4};
System.out.println("Before: " + Arrays.toString(arr));
new HeapSort().sort(arr);
System.err.println("After sorting: " + Arrays.toString(arr));
}
// 输出结果
Before: [11, 23, 44, 10, 3, 56, 3, 4]
After sorting: [3, 3, 4, 10, 11, 23, 44, 56]
2.3 排序操作时间空间复杂度
空间复杂度:由于没有引入额外的空间,所以空间复杂度为o(1)
时间复杂度:由于主要包含两个基本操作 - 调整成对结构 + 排序(调整)
第一步调整:o(nlogn) ;第二步主要在于调整节点及其子节点同样也为o(nlogn),所以其时间复杂度为o(nlogn)
3. 参考资料
【参考1】漫画:什么是堆排序?
作者:SV
出处:https://www.cnblogs.com/sv00
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
本文来自博客园,作者:seeviny,转载请注明原文链接:https://www.cnblogs.com/sv00/p/heapsort.html
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号