神秘构造题

Coloring Torus AGC030C：https://www.luogu.com.cn/problem/AT4512
考虑如果 \(k\le n\)，那么直接一行一种颜色就行了
如果 \(k>n\)，考虑可以转化为在对角线上染色，由于这个相邻的定义是循环的，所以合法：

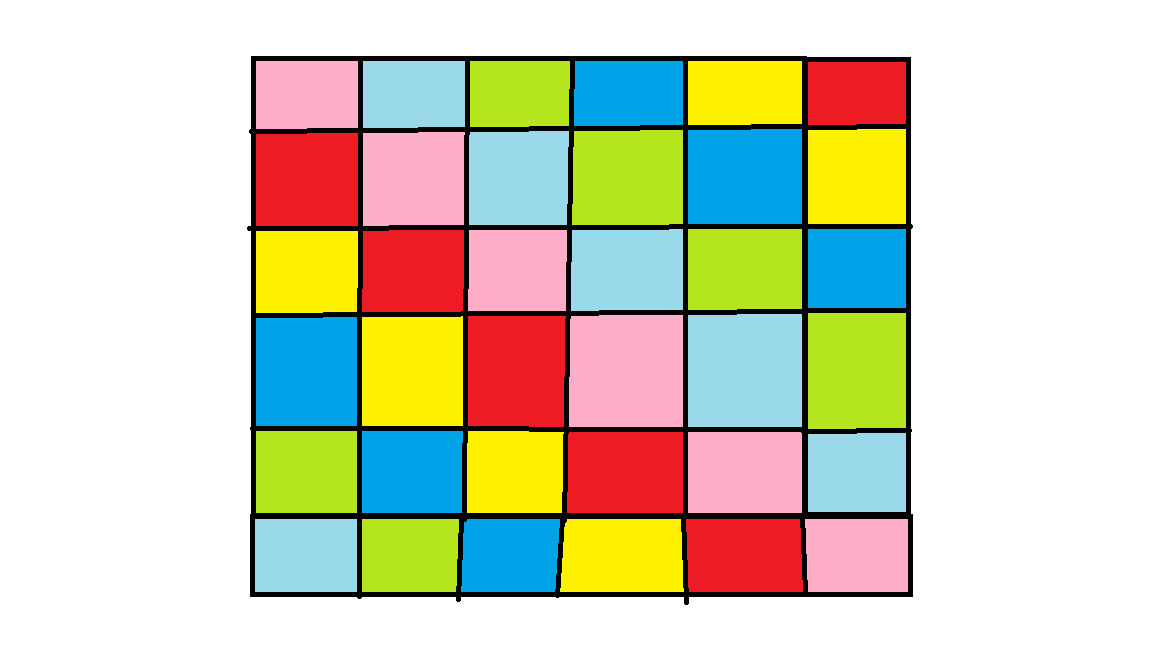
但这样仍然只能构造最多 \(n\) 中颜色，但发现可以把一部分对角线交替染色：

于是就可以了

Modulo Matrix AGC027D：https://www.luogu.com.cn/problem/AT4378
一个想法是先把格子黑板染色来分类，然后白点取它相邻的四个黑点的 \(\operatorname{lcm}+1\)
但这样如果在黑点上乱填的话值域仍然会炸
所以考虑对每一条穿过黑点的对角线（两个方向都算）确定一个质数，一个黑点的值就填两条穿过它的对角线的质数的乘积
然后就是如何确定这些质数的位置
先考虑所有从左上到右下的对角线，质数从小到大隔一条放一个，然后考虑从左上到右下的对角线，仍然是从小到大隔一条放一个
然后在重新考虑左上到右下的对角线，把那些没放的条再从小到大放上，左上到右下的也是同理
这样搞出来的有什么特点？就是由于质数是一个大一个小来放置的，所以同一个白点四周的四个黑点不会同时太大，也就不会乘炸了

Choosing Points AGC025D：https://www.luogu.com.cn/problem/AT3967
一个结论是平面上距离为 \(\sqrt{r}\) 的整点构成二分图
按照 \(r \bmod 4\) 分类，考虑 \(a^2+b^2=r\)（分别是横纵坐标的差值）

• \(r\equiv 3\pmod 4\)，没有符号要求的 \(a,b\)
• \(r\equiv 1\pmod 4\)，\(a,b\) 奇偶性不同，那么按棋盘的方式黑白染色
• \(r\equiv 2\pmod 4\)，\(a,b\) 都是奇数，隔行染色
• \(r\equiv 0\pmod 4\)，把 \(a,b\) 都缩小一半转化为上面的情况

于是在 \(\sqrt{D1}\) 的分类关系下能取出大小大于等于全集一半点
然后在这一些点中再按照 \(\sqrt{D2}\) 的分类关系取出大小大于等于全集四分之一的点

CF1270E Divide Points：https://www.luogu.com.cn/problem/CF1270E
给定 \(n\) 个点的坐标，给他们分组，若两个数字同组则用黄笔写下他们的距离，不同组则用蓝笔写下他们的距离。构造一组分组方案使得不存在一个数字被蓝笔和黄笔都写下过
\(n\le 10^3\)

先按照 \(x+y\) 给这 \(n\) 个点黑白染色，若同时存在黑点和白点，则直接按照黑白分组，此时黄数和蓝数平方和奇偶性必定不同
否则，把 \(n\) 个点绕原点旋转 45 度，在缩小 \(\sqrt{2}\)，再执行上面的判断，这样不会影响正确性

CF547D Mike and Fish
给定平面上 \(n\) 个整点，对其进行红蓝染色，使得同一水平或竖直直线上两种颜色数量差不超过 \(1\)
\(n\le 2\times 10^5\)

显然可以每一个水平和竖直直线建一个点，然后随便就能有连边跑上下界的方法（
显然 \(2\times 10^5\) 是网络流数据范围（

更好的方法也是把水平、竖直直线建点，分别记作 \(X_x,Y_y\)，把红点 \((x,y)\) 看作边 \(X_x\rightarrow Y_y\)，蓝点就反过来
然后要让每个点的出入度最多差 \(1\)
然后就可以建一个超级点向每个度数为奇数的点连一条边调节差距
那么问题就变成了取一条欧拉回路来定向

AGC017E Jigsaw

\(n\) 个形状如图的不规则图形，高度均为 \(h\)，横向三部分的宽度均为 \(1\)。现给定每一块的 \(a_i,b_i,c_i,d_i\)，将他们横着排列，使得每个图形的左右两个矩形的下边界都和地面或其他矩形的上边界紧密贴合，不能旋转或反转，问是否有解
\(n,h\le 10^5\)

显然应该从 \(c_i=0\) 或 \(d_i=0\) 的点入手，这些只用考虑他左或右边矩形的上边界，对于不为 \(0\) 的点，则只用考虑左或右边矩形的下边界
可以建立 \(2h\) 个点，让每块拼图作为一个边
让左边的矩形确定边的起点，如果其 \(c_i=0\)，起点是 \(a_i\)，否则是 \(c_i+h\)
让右边的矩形确定边的终点，如果其 \(d_i=0\)，终点是 \(b_i+h\)，否则是 \(d_i\)
然后这样建边如果能在边上走动就恰好对应着一段合法的拼接
然后建立一个超级点向所有的 \(c_i=0\) 的 \(a_i\) 发一条边，向所有 \(d_i=0\) 的 \(b_i+h\) 收一条边，然后一条欧拉回路就对应着一个合法方案

这两个题都是把题目的信息（\(n\) 个点之类的东西）转化成边，然后把信息之间的关系放在点上，根据关系连边，使得欧拉回路（让每个边被经过一次，也就是不能有不染色的点、不接入的拼图）对应一种合法方案

AGC037D Sorting a Grid
给定一个 \(n\times m\) 的矩阵 \(A\) , 保证 \(A\) 内的元素为 \(1\) 到 \(n\times m\) 的排列
将 \(A\) 每一行的元素任意排列得到 \(B\)
将 \(B\) 每一列的元素任意排列得到 \(C\)
将 \(C\) 每一行的元素任意排列得到 \(D\)
要求 \(D_{i,j}=(i-1)\times m+j\)，构造一组合法的 \(B,C\)
\(n,m\le 100\)

考虑从 \(D\) 还原到 \(C\)，那么第 \(i\) 行的所有元素都是在 \([(i-1)m+1,im]\) 之中
再从 \(C\) 还原到 \(B\)，如果把 \([(i-1)m+1,im]\) 的颜色定义为 \(i\)，则每一列包含所有颜色
所以此时就可以正着考虑能不能使得 \(A\) 变成 \(B\)，问题转化为共有 \(n\) 种颜色，每种颜色出现恰好 \(m\) 次，重排每一行使得每一列包含所有颜色
所以就每种颜色建一个点，每一行建一个点，行的点向他所包含的每种颜色连一条边，跑 \(m\) 次完美匹配，每次的结果就对应着每一列的构造方式，跑完把匹配到的边删掉就行了

AGC035C Skolem XOR Tree
给定 \(n\)，找到一个 \(2n\) 个节点的树，使得第 \(i,i+n\) 个点的点权为 \(i\)，且 \(i\) 到 \(i+n\) 的路径上的所有点的点权的异或和是 \(i\)
\(n\le 10^5\)

记 \(x'\) 表示 \(x+n\)
如果 \(n=2^k\)，那么无解，因为除了 \(n,n'\) 找不到其他的一些数使得他们的异或和为 \(n\)

考虑对于偶数 \(x\)，有 \(x\operatorname{xor} 1=x+1\)
可以这样构造，以 \(1\) 为根，对于每个偶数 \(x\)，将他和 \(x+1\) 搞成一个链挂在 \(1\) 的一个子树上
这样就有：\(x\rightarrow x+1 \rightarrow 1\rightarrow x'\)，以及 \(x+1 \rightarrow 1 \rightarrow x' \rightarrow (x+1)'\)
然后 \(1'\) 只有随便找个叶子挂在下面就行了，有：\(1\rightarrow x\rightarrow x+1\rightarrow 1'\)

但如果 \(n\) 是偶数就不好这样办，会剩下一个 \(n,n'\)
于是构造路径 \(n\rightarrow \operatorname{low}(n)\rightarrow 1\rightarrow (n-\operatorname{lowbit}(n)+1)'\rightarrow n'\)

CF527E Data Center Drama
\(n\) 个点 \(m\) 条边的无向图，需要加最少的边，然后再给图定向，使得每个点的出度入度都是偶数，允许重边自环
\(n\le 10^5,m\le 2\times 10^5\)

满足条件的图度数都是偶数，则一定存在欧拉回路，但这并不充分，不过可以按照这个想法先去搞
设原来有 \(k\) 个点度数是奇数，则至少需要加 \(\frac{k}{2}\) 条边才能使得每个点度数是奇数
这样搞完以后，可以走欧拉回路，在回路上按照正反正反的顺序定向
不过如果长度是奇数，回路回到起点以后导致起点的入度出度为奇数，所以再给这个点连一个自环就行了
显然这是最少的加边方案

AGC034D Manhattan Max Matching

给定 \(n\) 堆红点和 \(n\) 堆蓝点，位置分别是 \((rx_i,ry_i)\) 和 \((bx_i,by_i)\)，第 \(i\) 堆红点、蓝点分别有 \(rc_i\) 和 \(bc_i\) 个。保证 \(\sum rc_i=\sum bc_i=S\)
将红点蓝点两两匹配，设第 \(i\) 对红点蓝点的坐标为 \((x_{i1},y_{i1})\) 和 \((x_{i2},y_{i2})\)，构造匹配方案使得 \(\sum |x_{i1}-x_{i2}|+|y_{i1}-y_{i2}|\) 最大
\(n\le 1000,rc_i,bc_i\le 10\)

考虑点 \((x_1,y_1),(x_2,y_2)\) 之间的曼哈顿距离必然是这四种情况中的最大值：\((x_1-x_2)+(y_1-y_2)\)，\((x_1-x_2)+(y_2-y_1)\)，\((x_2-x_1)+(y_1-y_2)\)，\((x_2-x_1)+(y_2-y_1)\)
然后变化一下式子：\((x_1+y_1)+(-x_2-y_2)\)，\((x_1-y_1)+(y_2-x_2)\)，\((y_1-x_1)+(x_2-y_2)\)，\((-y_1-x_1)+(y_2+x_2)\)
所以可以建图：\(S\) 到 \(n\) 堆红点分别连边，\(n\) 堆红点向 \(p_1,p_2,p_3,p_4\) 四个新建点连边，边的费用分别是四种情况中 \(x_1,y_1\) 造成的贡献
然后这个四个点向 \(n\) 堆蓝点连费用为 \(x_2,y_2\) 的贡献的边，蓝点连向 \(T\)
跑最大费用最大流

CF1149E Election Promises
给定有向无环图，点有点权 \(w_i\)。两人轮流操作：取一个点 \(u\)，将其权值变成小于 \(w_u\) 的正整数，在对于边 \((u,v)\) 将 \(w_v\) 改成任意非负整数
不能操作的输。问先手是否必胜，以及必胜策略的第一步

定义 \(l_u=\operatorname{mex}\{l_v | (u,v)\in E\}\)，再设 \(val_i=\operatorname{XOR}_{l_u=i} w_u\)
这样分组以后可以发现，对于一个点 \(u\)，他连向的 \(v\) 中对于所有 \(i\in [0,l_u-1]\) 至少有一个 \(l_v=i\)
由此，可以得知对一个点 \(u\) 操作，可以将所有的 \(val_i,i<l_u\) 都变成 \(0\)
同时，如果 \(val_i=0\)，显然可以通过对 \(l_u=i\) 的任意一个 \(u\) 操作来使得 \(val_i\neq 0\)
那么通过这两个结论，就可以知道：

• 若存在一个 \(i\) 使得 \(val_i\neq 0\)，一定可以通过一次操作使得所有的 \(val_i=0\)。具体的方案就是找到最大的 \(i\) 使得 \(val_i\neq 0\)，对任意一个 \(l_u=i\) 的 \(u\) 进行一次操作，即可使得所有的 \(val_i=0\)
• 若对于任意 \(i\) 有 \(val_i=0\)，那么通过任意一次操作必然会使得一个 \(val_i\neq 0\)

那由此，即可得后手必胜当且仅当对于任意的 \(i\) 都有 \(val_i=0\)

AGC034E Complete Compress
给定 \(n\) 个节点的树，其中一些点上有棋子。每次操作可以指定两个距离至少为 \(2\) 的棋子，将他们往中间移动一下，问是否能把所有棋子聚集在一个点
\(n\le 2000\)

\(n\) 很小，可以先枚举最终聚集在哪个点
以聚集到的点为根，考虑“往中间移动”这个操作，如果这两个点在两个不同的子树上，则这两棵子树上 所以棋子到子树的根的距离和 都会减少一
而如果在同一子树上，如果移动两个有祖先关系的棋子，显然没有意义，因为移动完还需要和别的棋子一起移动才能往根上走
如果移动两个没有祖先关系的棋子，则这个子树中 所以棋子到子树的根的距离和 会减少二
那么记录 \(min_u,max_u\) 为对于以 \(u\) 为根的子树，对他进行任意操作后，所以棋子到子树的根的距离和 最小/最大值
考虑转移，对于 \(u\) 的所有子节点 \(v\)，显然有 \(max_u=\sum max_v\)，对于 \(min_u\)，设 \(min\) 最大的子节点为 \(p\)，如果 \(min_p\) 比其他的所有 \(max_v\) 加起来还大，那么 \(min_u=min_p-\sum_{v\neq p} max_v\)，否则根据奇偶性讨论 \(min_u\) 可以是 \(0\) 或 \(1\)
最后看 \(min_{root}\) 是不是 \(0\)

AGC038F Two Permutations
给定 \(0\) 到 \(n-1\) 的排列 \(P,Q\)，构造两个排列 \(A,B\)，使得 \(A_i=i\ or\ P_i,B_i=i\ or\ Q_i\)，并最大化 \(A_i\neq B_i\) 的数量

\(n\le 10^5\)

可以将 \(P,Q\) 看作由很多环组成，就是从 \(i\) 开始以 \(P_i\) 为下标找 \(P_{P_i}\)，然后一直找下去最后能回到 \(i\)
然后对于每个环，要么 \(A_i\) 在环上的位置都转一下：\(A_i=P_i\)；要么都不变：\(A_i=i\)
\(B\) 也是同理
然后用 \(x(i),y(i)\) 分别表示 \(i\) 这个位置的环，考虑对于以下几种情况 \(A_i=B_i\) 何时会出现

• \(P_i=Q_i=i\)，必定出现
• \(P_i=i\)，当 \(y(i)\) 不转时出现
• \(Q_i=i\)，当 \(x(i)\) 不转时出现
• \(P_i=Q_i\)，当 \(x(i),y(i)\) 同时转或不转时出现
• 其他情况，当 \(x(i),y(i)\) 都不转时出现

考虑建图，对于后四种情况分别连边：

• \(y(i)\rightarrow T\)
• \(S\rightarrow x(i)\)
• \(x(i)\rightarrow y(i),y(i)\rightarrow x(i)\)
• \(y(i)\rightarrow x(i)\)

然后可以看出每一条从 \(S\) 到 \(T\) 的路径，都存在至少其中的一条边对应的下标会出现 \(A_i=B_i\) 的情况，而跑最小割即可让这种情况出现次数最少