CF1149 简要题解

• A

注意到 \(\geq 3\) 的质数都是奇数，因此只要能构造出 \(3\)，则 \([3, \sum a_i]\) 间的每一个质数都可以构造出来，否则一定构造不出来。因此先尝试构造 \(3\)，后面先放 \(2\) 后放 \(1\) 即可。

• B

被出题人坑了（

注意题目中只保证任意时刻的串长 \(\leq 250\)，并不代表 trie 大小不超过 \(250\)，因此数组开小被爆了。（关键是它只显示 WA 不显示 RE 结果我对着 dp 的部分调了半天未果…… TvT）

首先可以预处理出母串的序列自动机（实际上就是每个位置出发的下一个字母各自最近的位置），可以做到 \(O(1)\) 在某个位置向后拓展一个字母。

设 \(f_{i, j, k}\) 表示三个串长度分别为 \(i, j, k\) 时，最后一个字母在母串中的位置最左是多少，\(n+1\) 表示无解。转移时只需枚举最后一个字母来自哪个子串即可。注意到串的变化只会在末尾产生，因此每次 push_back 一个字符的时候直接将包含新字符的 \(O(m^2)\) 个状态转移即可。复杂度 \(O(n\Sigma+m^2q)\)，其中 \(m\) 是最大串长。

• C

很有趣的题目。

直接从树的形态下手，会发现几乎没什么普适的规律。如果维护树的形态，每次操作可以达到 \(O(n)\) 的修改量（断边、连边等），不太可做。

但是实际上我们并不需要知道树的形态，只需要知道直径的长度。如果能想到树上两点 \((x, y)\) 路径长度是 \(d_x+d_y-2\cdot d_{\operatorname{lca}(x, y)}\) 的话，思路将会拓宽很多。考虑传统的求 LCA 方式，其中一种 \(O(n\log n)-O(1)\) 的方式是预处理欧拉序的 sparse table，不难发现 LCA 的深度是两点间唯一最小的那个。

因此，设欧拉序中第 \(i\) 个位置对应的点是 \(p_i\)，原问题实际上等价于求 \(\max_{1\leq i\leq j\leq 2n-1} d_{p_i}+d_{p_j}-2\cdot \min_{i\leq k\leq j} d_{p_k}\)。可以发现，里面的 \(\min\) 对答案的贡献需要取反，也就是说可以直接将它提取到外面的 \(\max\) 里处理：\(\max_{1\leq i\leq k\leq j\leq 2n-1} d_{p_i}+d_{p_j}-2\cdot d_{p_k}\)。再考虑一下每次修改操作，实际上是将某一步 “深度 \(+1\)” 和 “深度 \(-1\)” 交换了。因此，写出欧拉序上每个位置对应的深度（\(d_{p_i}\)）来，不难发现每次修改等价于区间 \(\pm 2\)。

上面的东西可以用线段树简单维护，复杂度 \(O(n\log n)\)。

• D

很有趣的题目。（\(\times 2\)）

考虑题目中最小生成树的限制，实际上等价于，先用 \(a\) 边将原图连成若干连通块并缩点，这样从 \(1\) 出发的路径都可以写出一个途径的连通块序列。题目要求我们，不能经过一个连通块多次（即离开连通块，经过若干条边后再返回这个连通块）。

首先将两端已经在同一个 \(a\) 连通块里的 \(b\) 边删掉，再考虑一下什么时候才会触犯这个条件。不难发现，如果最短路返回了某个离开过的 \(a\) 连通块，那么必然是从它出发，经过了至少 \(2\) 条 \(b\) 边（至少 \(2\) 条，因为两端在同一个 \(a\) 连通块里的 \(b\) 边已经被删了）和若干条（可能是 \(0\)）\(a\) 边后才回来。如下图：

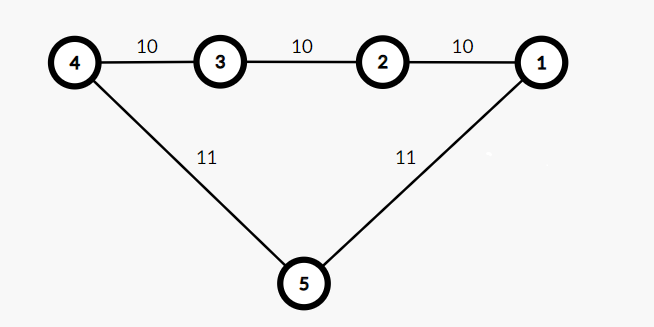
\(1\rightarrow4\) 的最短路本来应该是 \(1\rightarrow 5\rightarrow 4=22\)，但现在由于最小生成树的限制，无法走通。

由于 \(a<b\)，所以上面的不合法的过程至少需要跨越 \(3\) 条 \(a\) 边，才有可能更优。换句话说，我们重复经过的 \(a\) 连通块，至少有 \(4\) 个点。这个时候，我们发现 \(n\leq 70\) 的限制就非常和蔼可亲了——满足条件的连通块只有不超过 \(17\) 个，可以状压表示这些连通块是否访问过，即 \(f_{S, i}\) 表示访问过 \(S\) 内的连通块，当前停在 \(i\) 点的最短路。

预处理好在同一个 \(a\) 连通块内的点对 \((x, y)\) 之间的最短路 \(g_{x, y}\)，对于状压的每一个 mask，可以跑一遍 dijkstra，用 \(g_{x, y}\) 和 \(b\) 边更新别的点。复杂度 \(O\left(2^{\lfloor\frac{n}{4}\rfloor}\cdot (n^2+m)\right)\)，实际存在很多剪枝，大约只需要运行 1s。

• E

实际上这题 dls 在讲博弈论的时候讲过，是一道高阶无穷大裸题……

有些时候我们会遇到状态数无限的 nim 游戏，这个时候就需要引入高阶无穷大的概念。设 \(\omega\) 表示一个 \(1\) 阶无穷大，它能够转移到任意非负整数的状态。拓展一下，可以定义 \(k\omega\)，它能转移到任意 \(i\omega+j\)，其中 \(i\in [0, k-1], j\in \mathbb{N}\)。再拓展一下，定义 \(k\omega^p\) 可以转移到任意 \(j\omega^p+\sum_{i=0}^{k-1} a_i\cdot \omega^{i}\)，其中 \(j\in [0, k-1], a_i\in \mathbb{N}\)。

这个时候再回来看题目里的点。由于是拓扑图，必然存在出度为 \(0\) 的点，他们的 SG 值就是 \(h_i\)。假设某个点指向了一个出度为 \(0\) 的点，那么它至少是 \(1\) 阶无穷大。实际上，用简单的数学归纳法就可以证明，某个点 \(x\) 的阶数就是它指向的点集的阶数的 \(\operatorname{mex}\)。

对于包含高阶无穷大的 nim 游戏，先手必败当且仅当每一阶系数的异或和都是 \(0\)，构造和证明都与普通 nim 游戏类似。