CF1338 简要题解(已补完)
20.04.24 update:E 已更新
终于不 FST 了,舒服了。
趁着开心赶紧写一波题解(
- A
不难发现,在第 \(x\) 秒过完后,第 \(i\) 个数的取值范围是 \([a_i, a_i+2^x-1]\),并且其中的每一个整数都可以取到。因此,对于 \(a_i\),考虑所有 \(j<i\) 中,初始时最大的 \(a_j\),可以发现 \(a_j\) 最终恰取到 \(a_j\) 最优(因为不会存在 \(k<j, a_k>a_j\))。
所以,对于每一个 \(a_i\),设所有 \(j<i\) 中,初始时最大的 \(a_j\) 为 \(y\),则有 \(2^x\geq y-a_i+1\)。可以由此算出 \(x\) 的最小值。
- B
随便硬点一个根,设 \(d_i\) 表示 \(i\) 点到根路径上边权的 \(\operatorname{xor}\) 和,考虑每一对叶子 \((i, j)\) 之间的链,它的 \(\operatorname{xor}\) 和为 \(0\),实际上等价于 \(d_i \oplus d_{\operatorname{lca}(i, j)}\oplus d_j \oplus d_{\operatorname{lca}(i, j)}=d_i\oplus d_j=0\)。也就是说,我们要让每个叶子的 \(d_i\) 都相等。
首先考虑最小值。设 \(f_i\) 表示 \(i\) 到根路径上的边数。如果所有叶子 \(i\),\(f_i\) 的奇偶性均相等,我们显然可以将每一条边都标上相同的数字。否则,设正整数 \(x, y, z\) 满足 \(x\oplus y=z\),找到 \(f_k\) 最小的叶子 \(k\),将根到 \(k\) 路径上每一条边都赋上 \(z\) 的权值。按照 \(f_i\) 从小到大依次考虑其他叶子 \(i\),如果 \(f_i\not\equiv f_k\pmod 2\),就将 \(i\) 的父亲 \(p_i\) 相连的所有边中,连接 \(p_{p_i}\) 的边设为 \(x\),连接所有 \(p_i\) 的儿子的边设为 \(y\)。不难发现,这样等价于将 \(p_i\) 这个点以及它的连边缩成了一条权值为 \(z\) 的边,并使 \(p_i\) 子树中所有叶子的 \(f_i\) 都减少了 \(1\)。由于我们按照 \(f_i\) 从小到大地考虑所有叶子,必然可以构造出一组只使用了 \(x, y, z\) 的边(实际上不要求输出,这里只是借构造方式证明正确性)。由于所有权值都必须是正整数,可以发现只用两种权值无论如何也不能构造。
然后是最大值。由于可供使用的权值没有上限,因此对于任意的两条相邻的边,总可以给这两条边赋一个独一无二的权值,使得它们的异或和为任意正整数。唯一的问题是要求某两条相邻的边异或和为 \(0\) 的时候,此时不得不令它们权值相等。注意到这种情况只会发生在两个叶子之间距离为 \(2\) 时。因此,将所有这样的叶子缩到一起,最后剩下的每一条边都可以是独一无二的。缩叶子可以将它们挂在那个唯一相邻的点上。
注意,在根节点的度数为 \(1\) 时,根也是叶子。
- C
有趣的题目。
手玩一下最前面的几项,可以发现一些有用的性质:
- 对于所有 \(i\in [0, +\infty)\),恰有 \(2^{2i}\) 个三元组 \((a, b, c)\),满足 \(a\) 的最高位是 \(2^{2i}\),\(b, c\) 的最高位是 \(2^{2i+1}\),且 \(b\) 的第 \(2i\) 位是 \(0\),对应 \(c=a\oplus b\) 的第 \(2i\) 位是 \(1\)。
- 对于某个确定的 \(i\),将所有它对应的 \(2^{2i}\) 个三元组列出来,可以发现 \(a\) 恰好是按顺序排列的 \([2^{2i},2^{2i+1})\)。
- 为了让 \(c\) 不与之前出现过的重复,\(b\) 的最低位始终重复着 \(00, 10, 11, 01_{(2)}\)。
这几点都可以用数学归纳法简单证明。
实际上,性质 \(3\) 还有更多值得发掘的地方:对于 \(b\) 来说,它的每个相邻的两位 \((2^0, 2^1), (2^2, 2^3), \ldots\) 是相互独立的,而每两位内部则一直重复着 \(00, 10, 11, 01_{(2)}\)。当较低的某两位完成一次重复的时候,比它更高的相邻两位就会前进 \(1\) 格。实际上,由于在每段区间内的 \(a\) 是按顺序递增的,我们找到了一种对非负整数 \(b\) 的映射,使得映射后的第 \(i\) 个数满足 \(b_i\oplus i\) 两两不同。不难证明这是字典序最小的一种映射。
其实就是手玩/打表找规律
- D
实际上我 D 过得比较早,但是由于罚时太多(A+B+D 一共 \(5\) 发 \kk),排名就被甩了。不过还好没有 FST,赞美良心出题人的良心 pretest!
首先有一个十分显然的性质:被选为 nested 的点集一定是图中的某个独立集,因此答案不会超过树上点独立集的大小。
但是显然不会是最大点独立集这么简单对吧(
写了一发最大点独立集之后发现 WA on 2,于是考虑手动构造一个不大的反例,即答案小于最大点独立集的情况。但是在这之前我们要先知道,对于一个确定的独立集,如何尝试构造它的 rubber bands。
我们可以大体将点分为两类:被选为 nested 的和剩下的。对于 nested 的,我们只需要按照某种顺序排列这些套起来的圆,并将剩下的点抽象成连接这些圆的曲线。比如样例 \(1\) 大概长这样:
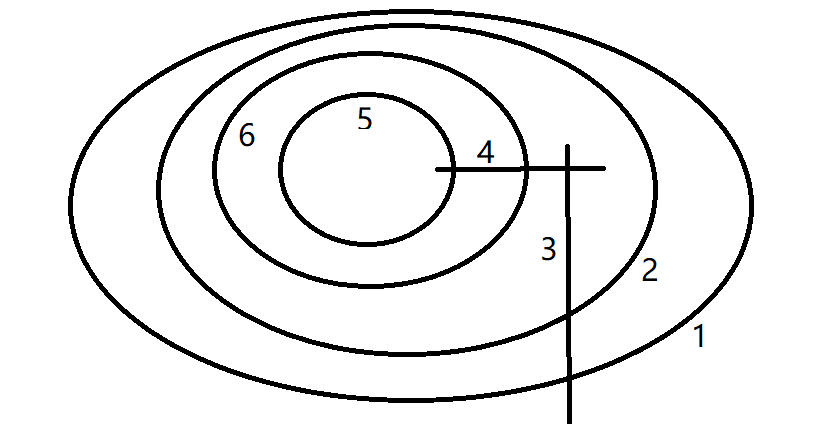
在经过了一段时间的尝试后,你可能会发现如下反例:

它的最大点独立集是 \(\{1, 3, 5, 7\}\),但是,将 \(1\) 作为一个圈画在图中时,你可以将 \(2-3\) 套在 \(1\) 的里面,将 \(4-5\) 套在 \(1\) 的外面。这时候你发现,不管你将 \(7\) 这个圈画在哪里,它都无法做到既和 \(2, 4\) 对应的线没有交点,又让 \(6\) 和 \(1\) 相连。实际上,观察一下画出来的图,你可以发现 \(1\) 这个圈的内侧和外侧已经被 \(2-3\) 和 \(4-5\) 组成的圈隔绝了,任何一条线,如果它另一端还连接着若干个圈(显然这些圈要么完全在 \(3\) 的内部,要么完全在 \(5\) 的外部,否则它将不可避免地与线 \(2/4\) 相交),都不可能在不穿过 \(3/5\) 的前提下与 \(1\) 相连。
因此,我们得到了两个规则:
nested的点集必然是原图的点独立集。- 如果某个点 \(i\) 被选为
nested,那么以 \(i\) 为根看待整棵树,最多只会有 \(2\) 个子树中包含nested的点。
我们还没有考虑根没有被选为 nested 的情况。乍一看,这种情况下,根的所有儿子都可以是 nested 的,只需要让根作为一条贯穿所有儿子的圈的线即可。于是我写了一发 WA on 4(
冷静下来仔细思考,我们发现了这个反例:
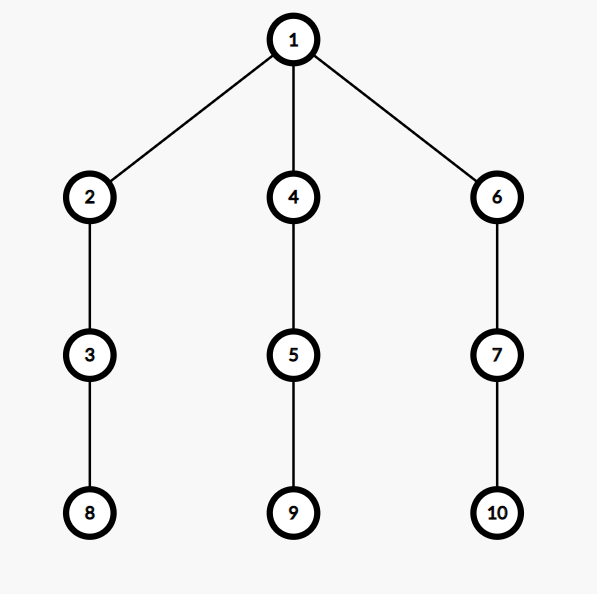
按照刚才的思路,我们应该选择 \(\{2, 4, 6, 8, 9, 10\}\),然而实际上这是不可能的。具体来说,我们大概能画出这样的图:
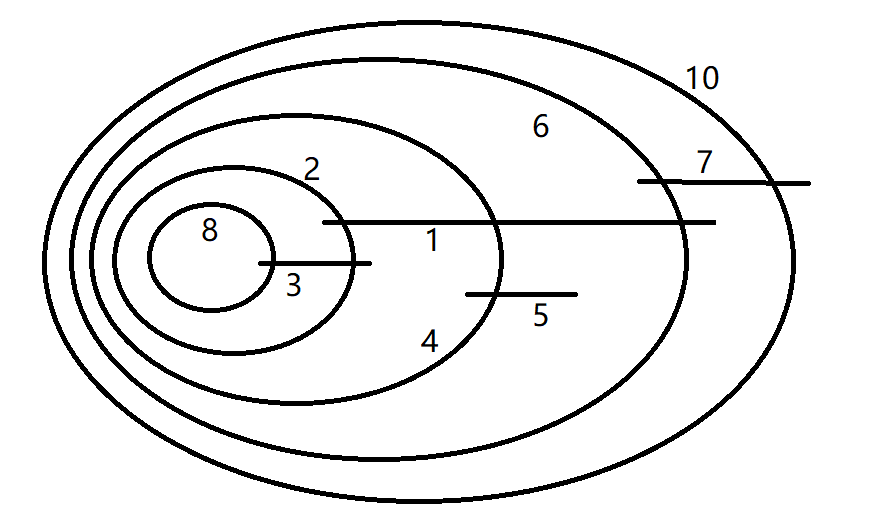
这时候,我们发现一件尴尬的事情—— \(9\) 没地方放了。不管怎么安排,如果 \(9\) 想以某种方式连接在 \(4-5\) 上的话,可以发现它必然会与 \(1\) 相连。仔细思考一下这种情况的本质,发现实际上是,如果某个点没有被选为 nested 的话,的确它所有的儿子都可以包含 nested 的点,但是实际上,只有被安排在最里面和最外面的两个儿子(圈),可以继续附带其他的圈(放在所有圈的内侧和外侧),剩下的所有儿子中的圈,都不可避免地与根节点相交。因此,我们得到了第三条规则:
- 如果节点 \(i\) 没有被选为
nested,那么以 \(i\) 为根看整棵树,最多只有两棵子树中可以包含更多的圈,其余子树都只有恰为 \(i\) 的儿子的那个节点可以成为一个圈,串在 \(i\) 这条线上。
有了以上三条规则,就可以做 dp 了。不难发现,对于不违反上面三条规则的点集,我们必然可以构造出合法的 rubber bands,因为这个点集大概的形状是一个长毛的链,直接从里到外按顺序套起来,再将剩下的线补齐即可。
诶这题居然是 \(2700\),我好强啊(逃
- E
不会,先咕着。
不咕了不咕了。
认真学习了一波官方题解,好强啊。
首先我们知道,多源最短路不管是 bfs 还是 Floyd,在本题都是铁打的 \(O(n^3)\),不可能过的。因此所有的性质都只能从题目里给出的保证来找。
这个保证看起来很抽象,思考一下,它到底保证了什么:对于一个点 \(x\),所有满足 \((y, x)\in E\) 的 \(y\) 组成的点集 \(S\) 满足 \(S\) 内无环。证明可以用数学归纳法,\(S\) 内显然不存在大小为 \(3\) 的环;如果存在一个长度 \(>3\) 的环,我们只需要随便找一个 \(a\rightarrow b\rightarrow c\),检查一下 \((c, a)\) 是否存在。如果存在显然不合法,否则有 \((a, c)\in E\),可以将 \(b\) 直接扔掉,环的长度减少了 \(1\)。
现在,让我们先进行一次拓扑排序,去掉所有入度为 \(0\) 的点并预先将它们的贡献算出来。不难发现,在竞赛图中,入度为 \(0\) 的点最多只有一个,并且它的出度必然为 \(m-1\),其中 \(m\) 是当前剩下的点数。由于它们能一步到达所有点,而其他点不可能走回来,每一个这样的点贡献都是 \((m-1)\cdot (1+614n)\)。
此时已经没有了入度为 \(0\) 的点,因此必然存在环。如果当前强连通分量的数量超过了 \(1\),则缩点后入度不为 \(0\) 的分量都不满足题目的保证。因此整张图只存在一个强连通分量。
假设我们当前选中了某个点 \(x\),我们可以将图中的点分为两个点集 \(S=\{y|(y, x)\in E\}\cup\{x\}, T=\{1, 2, \ldots, n\}-S\)。显然 \(S\) 内部不存在环,因此必然存在一个只考虑 \(x, y\in S, (x, y)\in E\) 的边时,入度为 \(0\) 的点 \(z\)。由于整张图里不存在入度为 \(0\) 的点,因此一定可以找到 \(y\in T, (y, z)\in E\) 的 \(y\) 点。设这些点组成的集合为 \(P\),显然 \(P\) 内部也不存在环。
这时候,我们梳理一下刚才定义的性质:由于 \(T\) 内的点 \(y\) 满足 \((y, x)\not \in E\),因此对于任意的 \(y\in T\),有 \((x, y)\in E\)。同理,设 \(Q=T-P\),则任意 \(y\in Q\),有 \((z, y)\in E\)。现在,任取 \(y\in Q, w\in P\),我们有 \((x, w), (w, z), (z, x), (x, y), (z, y) \in E\),只差 \((w, y)\) 这一条边,就产生了一种不合法的状态。因此 \((y, w)\in E\),即每个 \(Q\) 中点向 \(P\) 中点都有连边。由题目给出的保证可以知道,\(Q\) 内部也不存在环。
这个时候,不难发现,\(T\) 内部也是没有环的(它由两个没有环的点集拼成,并且点集之间的边都是 \(Q\rightarrow P\) 的)。
现在我们有了两个点集 \(S, T\),它们内部各自没有环,不妨将它们各自拓扑排序。设 \(S_i, T_i\) 表示只考虑端点都在点集中的边时,出度为 \(i\) 的点,即 \(S=\{S_0, S_1, \ldots, S_{|S|-1}\}\),\(T\) 同理。由一开始对 \(S, T\) 的定义可知,\(S_0=x\),且 \(\forall i\in \left[0, |T|\right), (S_0, T_i)\in E\)。
现在我们还需要知道对于 \(i\in \left[1, |S|\right)\),\(S_i\) 对 \(T\) 的连边情况。首先给出一个结论:对于 \(j\in \left[0, |T|\right)\),如果 \(( T_j, S_i)\in E\),则 \(\forall k\in\left[0, j\right], (T_k, S_i)\in E\)。证明可以用反证法,假设存在 \(k\in\left[0, j\right], (S_i, T_k)\in E\),由于 \((S_i, S_0), (S_0, T_j), (T_j, S_i)\in E\),组成了三元环,又有 \((S_0, T_k), (T_j, T_k)\in E\),必然会组成一种不合法的状态。
另外,设 \(p_i\) 表示最大的 \(j\),使得 \((T_j, S_i)\in E\),则 \(p_i\geq p_{i-1}\)。具体证明与上面类似,都可以构造出不合法状态。
update:应某位神仙要求,补上证明 \(p_i\geq p_{i-1}\) 的图。
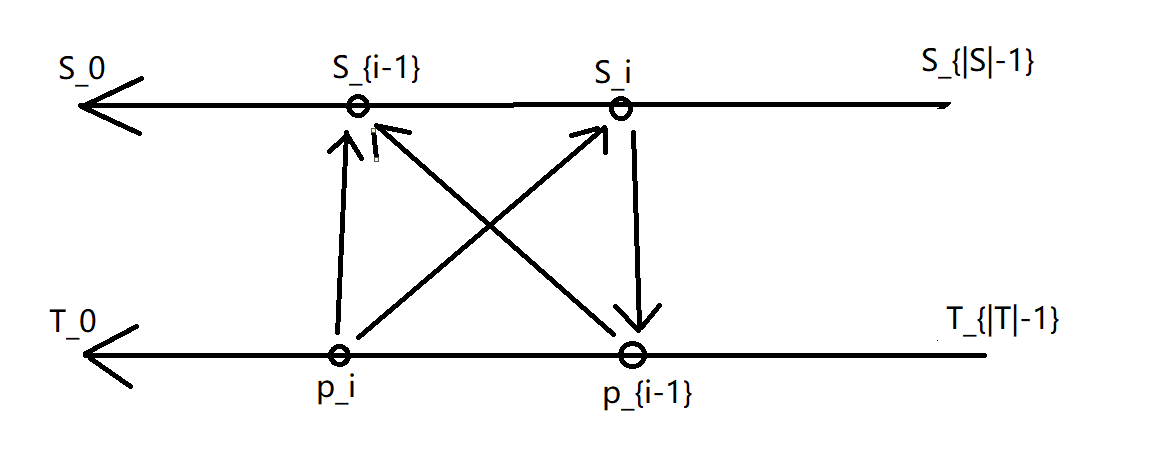
现在我们证明了对于每个 \(S_i\),\((T_j, S_i)\in E\) 的 \(j\) 是一个不减的前缀。实际上,对于每个 \(T_i\),类似地可以知道 \((S_j, T_i)\in E\) 的 \(j\) 也是一个不减的前缀。但是有一个问题是,我们知道 \((S_0, T_i)\in E\),也就是说,任意 \(S_j\),走到任意 \(T_i\) 的花费不会超过 \(2\)(\(S_j\rightarrow S_0\rightarrow T_i\))。但是我们并不能保证任意 \(T_i\) 走到 \(S_j\) 的花费。这个时候,留意到我们可以在选择最初的 \(x\) 时,选择在全集中入度最大的点作为 \(x\)。设它的入度为 \(d\),则 \(|S|=d+1\),并且任意 \(T_i\) 的入度都不大于 \(d\),也就是说,不存在这样的 \(T_i\),使得 \(\forall y\in S, (y, T_i)\in E\)。又由于 \((S_j, T_i)\in E\) 的 \(j\) 是个不减的前缀,必然有 \((T_i, S_{|S|-1})\in E\)。那么任意 \(T_i\) 走到 \(S_j\) 的花费也不会超过 \(2\)(\(T_i\rightarrow S_{|S|-1}\rightarrow S_j\))。
于是,经过一些简单的手动推导,我们可以得到,设 \(0\leq i<j\leq |S|-1\),有 \(\operatorname{dis}(S_j, S_i)=1, \operatorname{dis}(S_i, S_j)=2+[p_i=p_j]\),\(T\) 之间的同理。另外,\(\operatorname{dis}(S_i, T_j)+\operatorname{dis}(T_j, S_i)=3\)。所以整个问题可以 \(O(n^2)\) 解决了。


