HDU 2193 AVL Tree

　　AVL Tree

　　An AVL tree is a kind of balanced binary search tree. Named after their inventors, Adelson-Velskii and Landis, they were the first dynamically balanced trees to be proposed. Like red-black trees, they are not perfectly balanced, but pairs of sub-trees differ in height by at most 1, maintaining an O(logn) search time. Addition and deletion operations also take O(logn) time.
Definition of an AVL tree
An AVL tree is a binary search tree which has the following properties:
1. The sub-trees of every node differ in height by at most one.
2. Every sub-tree is an AVL tree.

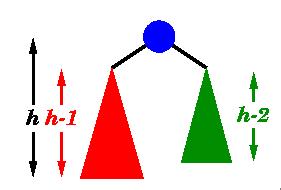
Balance requirement for an AVL tree: the left and right sub-trees differ by at most 1 in height.An AVL tree of n nodes can have different height.
For example, n = 7:

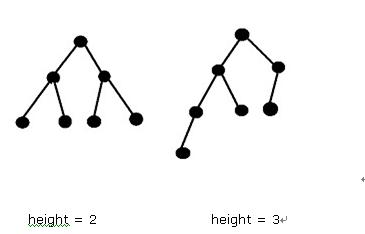
So the maximal height of the AVL Tree with 7 nodes is 3.
Given n,the number of vertices, you are to calculate the maximal hight of the AVL tree with n nodes.

Input

　　Input file contains multiple test cases. Each line of the input is an integer n(0<n<=10^9). 
A line with a zero ends the input. 
Output

　　An integer each line representing the maximal height of the AVL tree with n nodes.Sample Input

1
2
0

Sample Output

0
1

解题思路：
　　本题给出一个整数，要求输出其能建立的最高的平衡二叉树的高度。

　　关于平衡二叉树最小节点最大高度有一个公式，设height[i]为高度为i的平衡二叉树的最小结点数，则height[i] = height[i - 1] + height[i - 2] + 1；

　　因为高度为0时平衡二叉树：

　　#

　　高度为1时平衡二叉树：

0　　　　#　　或　　#

　　     /　　　　　　　  \

1　　#　　　　　　　　     #

　　

　　高度为2时平衡二叉树：

0　　　　　　#　　　　或　　　　#

　　　　     /　   \　　　　　  　  / 　　\

1　　　　#　　　  #　　　　　#　  　　#

　　 　/　　　　　　　　　　　　　　　  \

2　　#　　　　　　　　　　　　　　　　　#

　　高度为i时平衡二叉树：

　　　　　　#　　　　或　　　　#

　　　　    /　   \　　　　　  　  / 　　\

　　　　i - 2　  i - 1　　　　   i - 1　   i - 2

　　所以只需要将10^9内的数据记录后让输入的数据与之比较就可得到答案。（高度不会超过46）

 

#include <cstdio>
using namespace std;
const int maxn = 50;
int height[maxn];   
int main(){
    height[0] = 1;
    height[1] = 2;
    for(int i = 2; i < maxn; i++){  //记录1 - 50层最小需要多少节点
        height[i] = height[i - 1] + height[i - 2] + 1;
    }
    int n;
    while(scanf("%d", &n) != EOF){  //输入数据
        if(n == 0)  //如果为0结束程序
            break;
        int ans = -1;
        for(int i = 0; i < maxn; i++){  //从第0层开始比较
            if(n >= height[i])  //只要输入的数据大于等于该点的最小需求答案高度加一
                ans++;
            else
                break;  //否则结束循环
        }
        printf("%d\n", ans);    //输出答案
    }
    return 0;
}