HDOJ 1176 免费馅饼
免费馅饼
为了使问题简化,假设在接下来的一段时间里,馅饼都掉落在0-10这11个位置。开始时gameboy站在5这个位置,因此在第一秒,他只能接到4,5,6这三个位置中其中一个位置上的馅饼。问gameboy最多可能接到多少个馅饼?(假设他的背包可以容纳无穷多个馅饼)
Input
输入数据有多组。每组数据的第一行为以正整数n(0<n<100000),表示有n个馅饼掉在这条小径上。在结下来的n行中,每行有两个整数x,T(0<T<100000),表示在第T秒有一个馅饼掉在x点上。同一秒钟在同一点上可能掉下多个馅饼。n=0时输入结束。
Output
每一组输入数据对应一行输出。输出一个整数m,表示gameboy最多可能接到m个馅饼。
提示:本题的输入数据量比较大,建议用scanf读入,用cin可能会超时。
Sample Input
6 5 1 4 1 6 1 7 2 7 2 8 3 0
Sample Output
4
解题思路:
本题每组数据包括馅饼数量n之后n行给出每个馅饼的掉落时间与位置,有0-10共11个位置,起始在5位置,每次只能移动到周围两个位置,要求输出最大接到的馅饼数量。
本题类似数塔问题。
分析样例数据
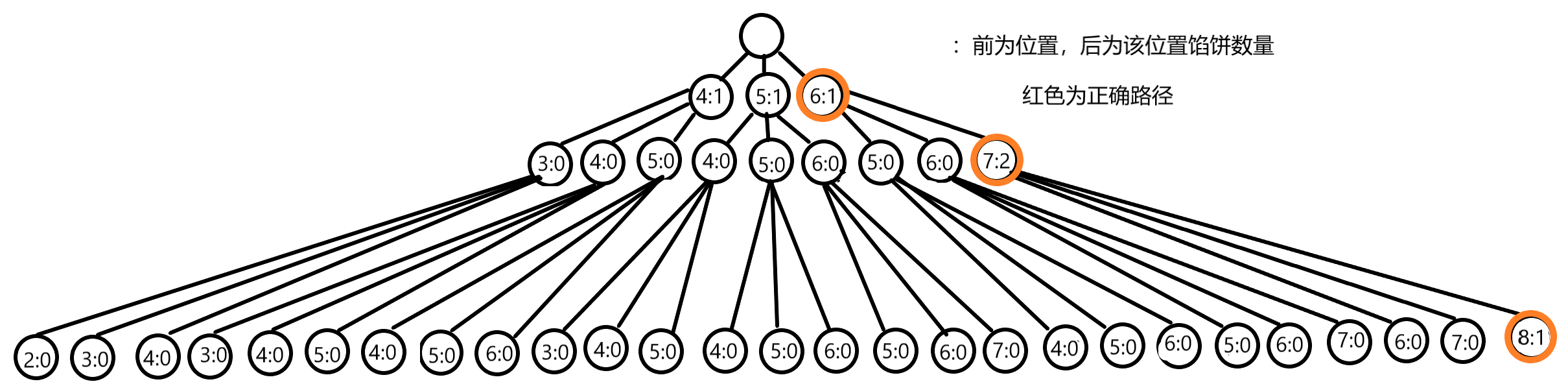
每个位置都可以抵达包括本身在内的3个位置我们用二维数组dp[ i ][ j ]表示如果第 i 秒在第 j 号位置,从开始到第 i 秒最多接到多少馅饼,与数塔问题一样都是找出一条路径,使路径上的权值和最大。
本着和数塔类似的拆解最低层的原则,该题形成的数塔的最底层为最后时间,样例中最后一个馅饼在第3秒落下,那么对于第三秒的某个位置j,如果第三秒gameboy刚好站在这个位置,那么其能接到的最大馅饼数量就是第三秒该位置掉落的馅饼数量加上其第二秒所在位置的最大获得馅饼数,而若在第三秒能抵达j位置,gameboy在第二秒一定是在j-1,j,j+1三个位置中的某一个,我们,只需要比较这三个位置的dp值并选择最大的一个即可获得第三秒j位置的dp值。
而求第二秒的三个位置的最馅饼数量又可以继续拆分为求第一秒所对应位置的最大馅饼数量,这样这个问题就可以被成功拆分了。
根据分析我们便可以写出动态转移方程dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + f[i][j]
AC代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e5+100; 4 int dp[maxn][12]; //dp[i][j]表示如果第i秒在第j号位置,从开始到第i秒最多接到多少馅饼 5 int f[maxn][12]; //f[i][j]的值第i秒j号位置上落下的馅饼数量 6 int main() 7 { 8 int n; //n为馅饼数量 9 while(scanf("%d", &n) != EOF && n){ 10 int maxtime = 0; 11 memset(dp, 0,sizeof(dp)); 12 memset(f, 0,sizeof(f)); 13 //每次运算dp与f初始化为0 14 for(int i = 0; i < n; i++){ 15 int time, x; 16 scanf("%d%d", &x, &time); //输入每个馅饼的掉落时间与位置 17 maxtime = max(maxtime, time); //记录最晚掉落的馅饼时间 18 f[time][x]++; //第time秒第x位置掉落的馅饼数量加一 19 } 20 dp[1][4] = f[1][4]; //由于第1秒接到4,5,6三个位置的其中一个位置的馅饼 21 dp[1][5] = f[1][5]; //所以若第一秒在哪个位置,第一秒最多接到的馅饼数量就是那个位置第一秒掉落的馅饼数量 22 dp[1][6] = f[1][6]; 23 int ans = 0; 24 for(int i = 2; i <= maxtime; i++){ //遍历从第二秒到最后掉落馅饼的那一秒 25 for(int j = 0; j < 11; j++){ 26 //动态转移方程 27 dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + f[i][j]; 28 //记录最大值 29 ans = max(ans, dp[i][j]); 30 } 31 } 32 printf("%d\n", ans); 33 } 34 return 0; 35 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号