HDU 1166 敌兵布阵(树状数组)

 敌兵布阵

　　C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手,但这些都逃不过C国的监视。 
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:"你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说："我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的. 

Input

　　第一行一个整数T，表示有T组数据。 
　　每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。 
　　接下来每行有一条命令，命令有4种形式： 
　　(1)Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30） 
　　(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）; 
　　(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数; 
　　(4)End 表示结束，这条命令在每组数据最后出现; 
　　每组数据最多有40000条命令 
Output

　　对第i组数据,首先输出“Case i:”和回车, 
　　对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。 
Sample Input

1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End 

Sample Output

Case 1:
6
33
59

解题思路：
　　本题有多组测试数据，给出测试数量t，元素个数n，之后给出一个有n个元素的整数序列a，之后给出操作语句以End为结束标值。

　　首先，对于查询一个整数序列前n个数之和，一般的做法是开一个sum[i]数组记录前i个整数之和可以将每次查询时间复杂度降至O(1)，但是在此处，Add与Sub操作随时可能对整除序列中的元素造成影响，假设更改了x号元素，若想继续维护sum数组就需要更新sum[x]、sum[x+1]、sum[x+2] …… sum[n]，这时虽然保证了查询的时间复杂度为O(1)，但是维护sum却需要O(n)的时间复杂度，对于本题来说是不可承受的。

　　这时便需要用到树状数组，我们用c[i]，来存放元素的和，c与sum的区别是，c[i]不是前i个元素的元素和而是下图的样子。

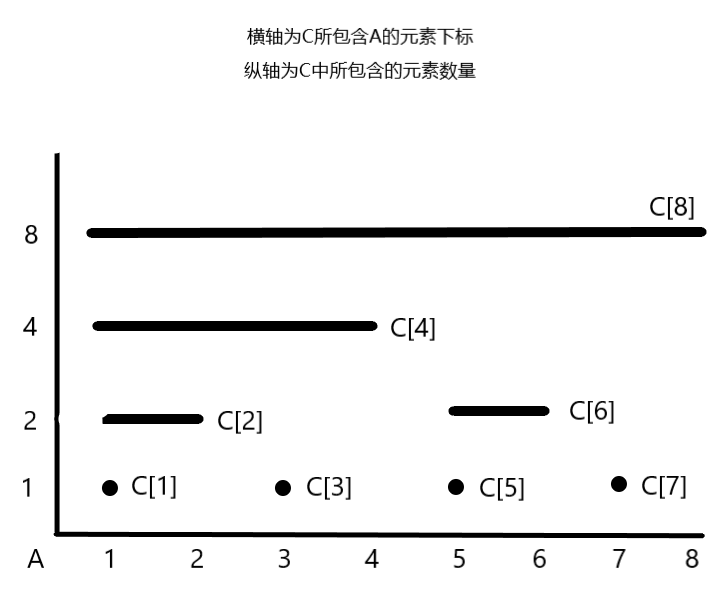
　　不难发现其中c[i]中的元素数量为i可以整除的最大的2的次幂数+1，我们称其为lowbit( i )。

　　如何快速计算出lowbit？如果了解计算机组成原理可以得知，整数在计算机中的存储采用的是补码，若把 i 的二进制位每一位都取反后末位+1，便可得到-i，，这其实相当于把 i 的二进制位右起第一个1左方的所有位取反，之后 i &( -i )便可取得最右位的1与其右方所有的0，这显然是2的次幂。这样我们就获得了lowbit( i )，例如12（1100）取反（0011）加一（0100），最右方的1与其右方的0（100）= 4。

　　根据上图分析数组c。

长度：1 c[1] = a[1]
长度：2 c[2] = a[1] + a[2]                                         = c[1] + a[2]
长度：1 c[3] = a[3]
长度：4 c[4] = a[1] + a[2] + a[3] + a[4]                           = c[2] + c[3] + c[1] + a[4]
长度：1 c[5] = a[5]
长度：2 c[6] = a[5] + a[6]                                         = c[5] + a[6]
长度：1 c[7] = a[7]
长度：8 c[8] = a[1] + a[2] + a[3] + a[4] + a[5] +a[6] + a[7] +a[8] = c[4] + c[6] + c[7] + a[8]

　　由于c[ i ]的长度为lowbit( i )可以总结出c[ i ] = a[i - lowbit( i ) + 1] + a[i - lowbit( i ) + 2] + …… + a[ i ]。

　　从1 ~ i a的和为a[1] + a[2] + a[3] + …… + a[ i ]，将它疯狂拆分。

  a[1] + a[2] + a[3] + …… + a[ i ]
= a[1] + a[2] + a[3] + …… + a[i - lowbit(i)] + a[i - lowbit(i) + 1] + …… + a[ i ]
= a[1] + a[2] + a[3] + …… + a[i - lowbit(i)] + c[i]
= a[1] + a[2] + a[3] + …… + a[ (i - lowbit(i) ) - lowbit(i - lowbit(i)) ]  + c[i - lowbit(i)] + c[ i ]

　　找到了规律，获得了巨大的快乐。

　　之后我们写出获取从1 ~ i a的元素和的函数，至于题中要查询i ~ j的元素和，我等只需要查出1 ~ j的元素和与1 ~ i - 1的元素和即可，这样我们只需要O(logn)的时间复杂度就可以完成一次查询。

getSum函数：

int getSum(int x){
    int sum = 0;    //sum记录和
    for(int i = x; i > 0; i -= lowbit(i)){  //拆分每一个C[i]
        sum += C[i];    //累计C[i]将求和范围缩小至
        //a[1] + a[2] + a[3] + …… + a[i - lowbit(i)] + c[i]
    }
    return sum;
}

　　解决了查询的问题就要开始处理题目中要求的加与减了。

　　如果我们想将a[ i ]加或减去一个数值，那么我们需要将所有包含a[ i ]的c[ i ]都加上或减去一个同样的值。

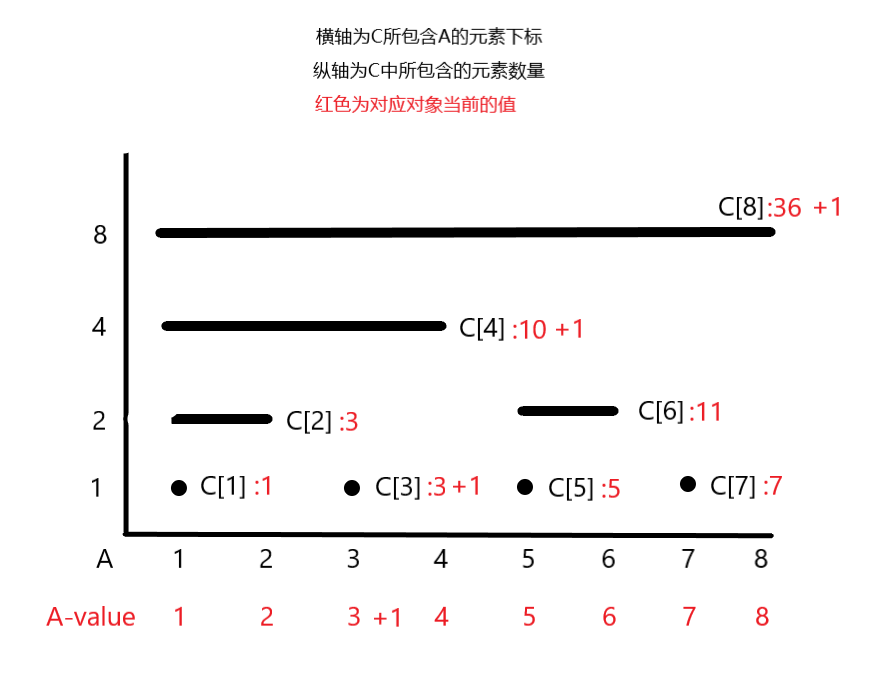
　　也就是说若将a[3] + 1对应的c[3] c[4] c[8]都要+1，我们要想办法确定覆盖c[3]的最近的c[x]，由于c[x]中每个元素包含的a的数量为lowbit(x)，若想让c[x]包含c[3]，那必定lowbit(x) > lowbit(3)，否则不可能覆盖。之后我们设x = 3 + y，当y = 3时根据我们之前对lowbit来源的解释，3 与 y相等，它们转化为二进制后最右方的1的位置一定相等，x 的最右方1的位置即为y最右方1左侧的第一个0的位置，那么lowbit(x)定然大于lowbit(3)，即x = 6时，这个3 + lowbit(6) = 4就是我们能找到的第一个包含c[3]的c的元素。

　　之后我们便可以写出更新函数update

void update(int x, int v){  //传入要更改的元素位置与要更改的数值
    for(int i = x; i <= n; i += lowbit(i)){ //让找到的每一个c[i]都加上v
        C[i] += v;
    }
}

　　有了getSum与update函数我们就可以做到本题一切要求了。

　　之后只需要根据输入的是Query、Add还是Sub进行操作即可。

AC代码

#include <bits/stdc++.h>
#define lowbit(i) ((i)&(-i))
using namespace std;
const int maxn = 5e4+100;
int c[maxn];
void update(int x, int v){//传入要更改的元素位置与要更改的数值
    for(int i = x; i < maxn; i += lowbit(i)){//让找到的每一个c[i]都加上v
        c[i] += v;
    }
}
int getSum(int x){
    int sum = 0;    //sum记录和
    for(int i = x; i > 0; i -= lowbit(i)){  //拆分每一个C[i]
        sum += c[i];
        //累计C[i]将求和范围缩小至a[1] + a[2] + a[3] + …… + a[i - lowbit(i)] + c[i]
    }
    return sum;
}
int main()
{
    int n, x, t;
    while(scanf("%d", &t) != EOF){  //输入测试数量
        int cnt = 1; //cnt记录当前测试编号
        while(t--){
            scanf("%d", &n);    //输入敌人工兵营地数量
            memset(c, 0, sizeof(c));    //初始化数组0的元素值都为0
            for(int i = 1; i <= n; i++){
                scanf("%d", &x);    //输入每个营地的初始人数
                update(i, x);   //更新c[i]增加x个人
            }
            string s;   //s记录输入的命令
            printf("Case %d:\n", cnt++);
            while(1){
                cin >> s;
                if(s == "Query"){   //查询
                        int a, b;
                        scanf("%d%d", &a, &b);
                        int ansa, ansb;
                        ansa = getSum(a - 1);
                        ansb = getSum(b);
                        printf("%d\n", ansb - ansa);
                }else if(s == "Add"){   //增加
                    int a, b;
                        scanf("%d%d", &a, &b);
                        update(a, b);
                }else if(s == "Sub"){   //减少
                    int a, b;
                        scanf("%d%d", &a, &b);
                        update(a, -b);
                }else{  //收到End结束
                    break;
                }
            }
        }
    }
    return 0;
}