Codeforces 450B Jzzhu and Sequences

　　Jzzhu and Sequences 

　　Jzzhu has invented a kind of sequences, they meet the following property:

　　You are given x and y, please calculate f_n modulo 1000000007 (10⁹ + 7).

Input

　　The first line contains two integers x and y(|x|, |y| ≤ 10⁹). The second line contains a single integer n (1 ≤ n ≤ 2·10⁹).

Output

　　Output a single integer representing f_n modulo 1000000007 (10⁹ + 7).

Examples

Input

2 3
3

Output

1

Input

0 -1
2

Output

1000000006

Note

　　In the first sample, f₂ = f₁ + f₃, 3 = 2 + f₃, f₃ = 1.

　　In the second sample, f₂ =  - 1;  - 1 modulo (10⁹ + 7)equals (10⁹ + 6).

解题思路：
　　本题给出一个运算公式 f( i ) = f( i - 1) + f(i + 1)给出两个整数分别为前两项的值，之后给出一个整数n，要求求出第n项的值。

　　我们首先将公式变形一下

　　

     f( i ) = f( i - 1 ) + f( i + 1 ) 
 ⇔  f( i + 1 ) =  f( i ) - f( i - 1 )
 ⇔  f( i ) = f( i - 1 ) - f( i - 2 )

　　之后我们将相邻两项计入一个2 * 1的矩阵中

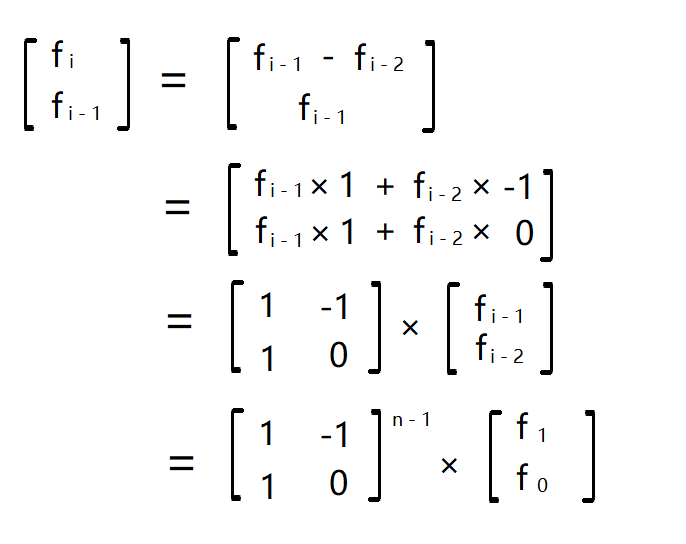
　　n大于3时计算n - 2次方即可得出答案

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 1e9+7;
const int maxn = 2;
struct matrix{
    LL mat[maxn][maxn]; //mat存放矩阵
    matrix operator *(const matrix &a)const{    //重载运算符*
        matrix ans;
        for(int i = 0; i < 2; i++){ //遍历行
            for(int j = 0; j < 2; j++){ //遍历列
                ans.mat[i][j] = 0;
                for(int k =0; k < 2; k++){  //固定k进行矩阵乘法
                    ans.mat[i][j] = (ans.mat[i][j] + mat[i][k] * a.mat[k][j] % mod) % mod;
                }
            }
        }
        return ans;
    }
};
matrix power(matrix a, LL b){   //矩阵快速幂，与普通快速幂几乎没有区别
    matrix ans; //答案矩阵
    memset(ans.mat, 0, sizeof(ans.mat));    
    for(int i = 0; i < 2; i++){
        ans.mat[i][i] = 1;
    }
    //以上为初始化单位矩阵
    while(b){
        if(b & 1){  //b按位与1匹配
            ans = ans * a;
        }
        b >>= 1;
        a = a * a;
    }
    return ans;
}
int main()
{
    LL x ,y, n;

    while(scanf("%lld%lld", &x, &y) != EOF){    //输入x与y
        matrix a;
        scanf("%lld", &n);  //输入n
        a.mat[0][0] = 1;
        a.mat[0][1] = -1;
        a.mat[1][0] = 1;
        a.mat[1][1] = 0;
        //初始化矩阵
        //n为1或2单独判断
        if(n == 1){
            printf("%lld\n", (x % mod + mod) % mod);
        }else if(n == 2){
            printf("%lld\n", (y % mod + mod) % mod);
        }else{  //n>=3
            a = power(a, n - 2);    //计算矩阵a的n - 2次方
            LL ans = (((a.mat[0][0] * y + a.mat[0][1] * x) % mod) + mod ) % mod;
            
            printf("%lld\n", ans);
        }
    }
    return 0;
}

 

 

[FnFn−1]=[Fn−1+Fn−2Fn−1]=[Fn−1×1+Fn−2×1Fn−1×1+Fn−2×0]=[1110]×[Fn−1Fn−2]=[1110]n−1×[F1F0]=[1110]n−1×[10]