【计算摄影学】双边滤波通俗理解以及简单实现

概念

双边滤波是非常常用的一种滤波，在前面我们已经实现了三种滤波：均值滤波、高斯滤波与中值滤波。这三种滤波都能够在一定程度上消除噪声，但是其作用范围有限，只能针对特定种类的噪声。例如高斯滤波针对高斯噪声效果较好，而中值滤波针对椒盐噪声的效果较好。而且，这三种滤波对图像的边缘信息都会有不同程度的损坏，究其原因是没有考虑到图像边缘的信息。因而，我们引入双边滤波，其在利用高斯滤波去噪的同时，能够较好地保存图片的边缘信息。如果你还没有理解高斯滤波，请参考我的这篇博文：https://www.cnblogs.com/suubai/p/12484025.html

一般而言，区分图像是否为边缘部分的方法如下：

• 在图像的边缘部分，像素值的变化较为剧烈。
• 在图像的非边缘区域，像素值的变换较为平坦。

通过以上两点，我们可以总结出，想要保留图像边缘，必须引入一个能够衡量图像像素变换剧烈程度的变量。由此，我们引入了图像像素域核G_r。

首先看双边滤波的公式：

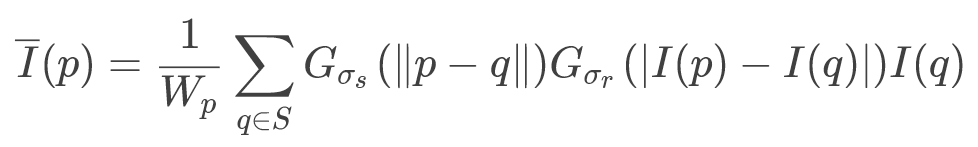
其中，W_p为：

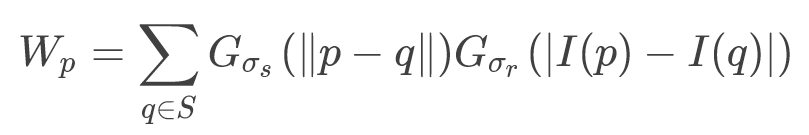
好像开始复杂了起来，那么这两个反人类的表达式究竟是什么意思呢？不要急，接下来我们开始慢慢剖析。

首先我们要知道，双边滤波中有两个衡量图像信息的核心变量，如上式中的G_σs为空间域核，G_σr为图像像素域核。空间域核其实就是二维高斯函数，可以把它视作高斯滤波，像素域核就是衡量像素变化剧烈程度的量。将这两个变量相乘，就可以得到他们俩共同作用的结果：在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊；在图像的边缘区域，像素值变化很大，像素范围域权重变大，从而保持了边缘的信息。

那么具体怎么求解图像的双边滤波呢？首先我们需要知道空间域核计算方法：

  

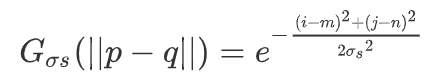
以及像素域核的计算方法：

 

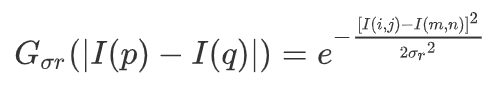
 在上面两个式子中，σ_s与σ_r都是已知的，或者说是自己输入的预设值，而其他的i，j，m，n都是需要我们在遍历中确定的值。其中（i，j）代表是窗口中心值，（m，n）代表的是滑动窗口中的某个值。

我们知道图像滤波大多数都是卷积的结果，对于双边滤波，其不仅仅是卷积那么简单。但是和卷积类似，都是需要一个滑动窗口来作用于整个图像。如下图所示：

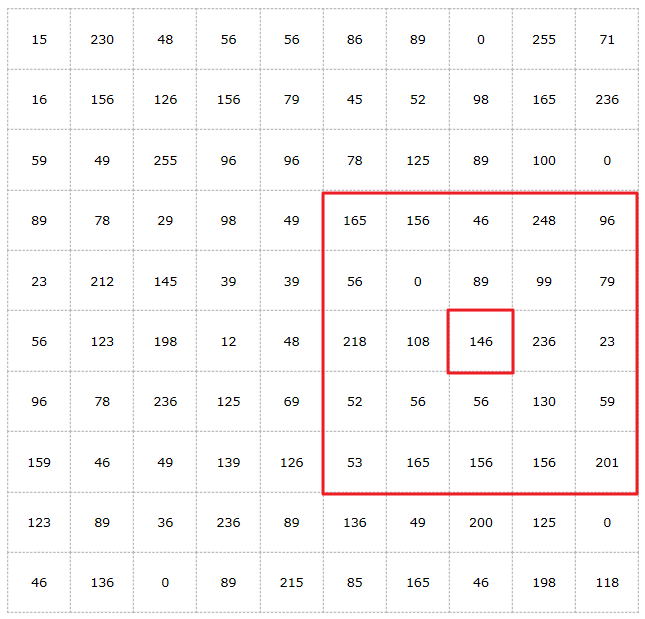
 整张图可以看作是10 × 10的一张图像，图中的数字表示每个点的像素值。在图中存在一个5 × 5大小的滑动窗口，我们需要求出中心点146的新像素值。

• 首先遍历整个窗口，第一个遍历到的点是165，那么中心点与该点的空间域计算结果为：

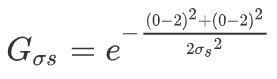
• 再计算中心点与该点的像素域结果：

• 当 σ_s 与 σ_r 分别为5和20时，G_σs = 0.8521，G_σr = 0.6368。
• 接着遍历整个窗口，将窗口内每个像素点都与中心点建立联系，求出它们的 G_σs 与 G_σr 的值，将 G_σs 与 G_σr 相乘即得到每个点对应的W_p，即W_p = G_σs × G_σr。
• 在遍历结束后，用每个点的W_p乘上该点的像素值I(m, n)，并求和，这是作为分子。将每个点的W_p相加，作为分母，两者相除，即得到需要的新输出图像的中心点（i，j）的像素值。

至此，大功告成。需要注意的是，如果是RGB三通道的图像，每个点的像素值就需要将RGB三通道分开求解。

 

理论分析

求解双边滤波的过程如下：

• 读取原始图像。
• 设定窗口大小，遍历整个图像，将窗口覆盖内的所有像素值与窗口中心像素比对，求取空间域核与图像像素域核大小，并将两者相乘作为该点的特征值。
• 将每一点的特征值与该点像素值乘积相加，除以所有特征值的和，得到的结果即作为中心点的像素值。

在求解过程中，需要注意的是，如果是RGB三通道的图像，每个点的像素值就需要将RGB三通道分开求解。

 

实验细节

遍历图像求解特征值

// 遍历图像
for (int i = 0; i < src.rows; i++) {
    for (int j = 0; j < src.cols; j++) {
        double fenzi_r, fenmu_r, fenzi_g, fenmu_g, fenzi_b, fenmu_b;
        fenzi_r = fenmu_r = fenzi_g = fenmu_g = fenzi_b = fenmu_b = 0;

        for (int m = i - window_size; m <= i + window_size; m++) {
            for (int n = j - window_size; n <= j + window_size; n++) {
                if (!(m<0 || m>src.rows - 1 || n<0 || n>src.cols - 1)) {
                    // 该条件排除了窗口内的图像边界外部值
                    double w = exp(-(1.0f)* (((m - i) * (m - i) + (n - j) * (n - j)) / (2.0f*sigma_s*sigma_s)));
                    double w_r = exp(-(1.0f)* (pow((double)(src.at<Vec3b>(i, j)[2] - src.at<Vec3b>(m, n)[2]), 2) / (2.0f*sigma_r*sigma_r)));
                    double w_g = exp(-(1.0f)* (pow((double)(src.at<Vec3b>(i, j)[1] - src.at<Vec3b>(m, n)[1]), 2) / (2.0f*sigma_r*sigma_r)));
                    double w_b = exp(-(1.0f)* (pow((double)(src.at<Vec3b>(i, j)[0] - src.at<Vec3b>(m, n)[0]), 2) / (2.0f*sigma_r*sigma_r)));
                    fenmu_r += w * w_r;
                    fenmu_g += w * w_g;
                    fenmu_b += w * w_b;
                    fenzi_r += w * w_r*(double)src.at<Vec3b>(m, n)[2];
                    fenzi_g += w * w_g*(double)src.at<Vec3b>(m, n)[1];
                    fenzi_b += w * w_b*(double)src.at<Vec3b>(m, n)[0];
                }
            }
        }

        dst.at<Vec3b>(i, j)[2] = (double)fenzi_r / (double)fenmu_r;
        dst.at<Vec3b>(i, j)[1] = (double)fenzi_g / (double)fenmu_g;
        dst.at<Vec3b>(i, j)[0] = (double)fenzi_b / (double)fenmu_b;
    }
}

 该部分为整个程序的主体部分。在该部分中，遍历图像的每一点，再在内部遍历以该点为中心点的窗口内部所有点。直接用公式求出每一点相对中心点的空间域的值，然后分为RGB三个通道求出像素域值。直接用分子、分母作为变量名，求出三个通道的所有需要的分子分母。在窗口循环结束后，直接作除法并赋值给目标输出图像即可。

 

成果展示

（原始图像）

（双边滤波处理图像，σ_s = 5，σ_r = 20）