【计算摄影学】高斯滤波的简单实现

概念

通常我们认为图像像素之间的相关性随着距离增加应该不断减弱，但是均值滤波并没有体现这一性质。在对图像进行均值滤波时，如果图像中有一些很显著的亮点，滤波后它的周围会形成光斑。这正是因为均值滤波无视了距离，对很远处的像素依旧采用同样的权重导致的。一些场合，我们为了美感会需要这种效果。另一些场合，这种结果是不利的，特别是在做图像处理时。因此我们引入了具有距离权重的高斯滤波。

通常而言，高斯函数可以分为一维和二维，一维高斯函数更广为人知，其就是正态分布的表达式。而二维高斯滤波则具有和一维相似的性质：

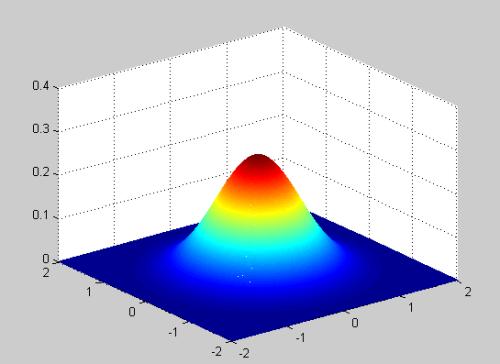
由二维高斯函数的图形，我们很容易看出，若用其作为卷积核，那么越靠近中心的像素相关性越大。在进行高斯滤波时，就是将二维高斯函数作为卷积核，对图像进行滑窗卷积。二维高斯函数的表达式如下：

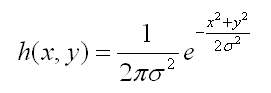
毫无疑问，卷积核通常是奇数长宽的窗口，以便于确定中心。高斯滤波的卷积核一般采用正方形，3 × 3或5 × 5甚至更大。由于高斯函数的高度对称性，取正方形作为卷积核是不难理解的。在本实验中，我们将高斯函数的卷积核大小设置为：

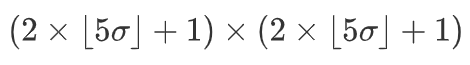
下面我们以3 × 3大小的卷积核为例，介绍具体如何求取卷积核的数值。在模板的各个位置的坐标如下图所示（x轴水平向右，y轴竖直向上）：

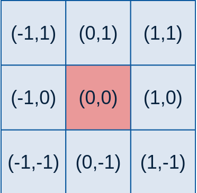
这样，将各个位置的坐标（x，y）代入到高斯函数G中，得到的每个值按照位置排列，就得到了模板。

例如：生成高斯核为3 × 3，σ = 0.8的模板：

0.057118	0.12476	0.057118
0.12476	0.2725	0.12476
0.057118	0.12476	0.057118

 

 

 

 

从以上描述中我们可以看出，高斯滤波模板中最重要的参数就是高斯分布的标准差σ。它代表着数据的离散程度，如果σ较小，那么生成的模板中心系数越大，而周围的系数越小，这样对图像的平滑效果就不是很明显；相反，σ较大时，则生成的模板的各个系数相差就不是很大，比较类似于均值模板，对图像的平滑效果就比较明显。

 

理论分析

 求解图像的高斯滤波与均值滤波的步骤相似，可以分为如下几步：

•  读取原始图像
•  求出高斯滤波的卷积核
•  利用 filter2D 函数进行卷积操作
•  写入高斯滤波后的图像

高斯滤波与均值滤波对比，主要的不同在于第二步求解卷积核，相比而言高斯滤波卷积核的求解稍微复杂一些。

 

实验细节

1、卷积核的求取

// 初始化高斯卷积核
kernel = Mat::ones(kHeight, kWidth, CV_32F);

// 找到高斯核的中心点
// 注意该中心点是以0开头，10σ结尾的中心点
int center = floor(5 * sigma);

// 遍历Mat，求值
for (int i = 0; i < kHeight; i++) {
    for (int j = 0; j < kWidth; j++) {
        // 坐标（i，j）对应的高斯坐标系中的坐标为(i - center, center - j)
        double x = i - center;
        double y = center - j;
        kernel.at<float>(i, j) = 1.0f / (2.0f * pi*sigma*sigma)*exp(-(1.0f)* ((x * x + y * y) / (2.0f*sigma*sigma)));
        cout << kernel.at<float>(i, j) << "\t\t";
    }
    cout << endl;
}

代码如上，由用户输入的σ，上面又规定了卷积核的大小，因此很容易确定卷积核的中心为：

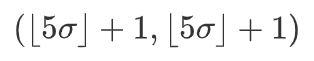
在真实的代码环境中，由于下标默认为0开始，因此卷积核的中心可以将最后的+1去掉。此时，将该中心设置为原点（0，0），对整个Mat进行遍历，对于掩膜矩阵中的每一个点（i，j），其在高斯坐标系中对应的（x，y）坐标为（i - center，center - j），直接套用高斯函数的公式即可求解出掩膜中每一个点的数值。这样就得到了我们想要的高斯卷积核。

2、利用 filter2D 函数进行卷积操作

与均值滤波类似，直接用filter2D进行卷积操作即可：

Point anchor(-1, -1); //中间的点
int depth = -1;       //深度和输入一样
int delta = 0;        //在处理之后　再加上delta,默认0

filter2D(src, dst, depth, kernel, anchor, delta);

 

结果展示

                                                                （原始图像）

                                               （高斯滤波输出图像，取σ = 0.8）

 

最后附上完整代码：

#include<opencv2/opencv.hpp>
#include<iostream>
using namespace std;
using namespace cv;
#define pi 3.1415926535

int main()
{
    Mat src, dst;
    Mat kernel;
    string image_name;
    string output_name;
    int kHeight, kWidth, img_height, img_width;
    double sigma;

    cout << "请输入需要读取的图像名称：";
    cin >> image_name;

    cout << "请输入输出的图像名称：";
    cin >> output_name;

    cout << "请输入需要的sigma：";
    cin >> sigma;

    // 进行初始判断
    src = imread(image_name, IMREAD_COLOR);
    if (src.empty()) {
        cout << "图像读取失败！" << endl;
        return 0;
    }
    else {
        // 若读取成功，判断卷积核的大小与图像大小的关系
        kHeight = 2 * floor(5 * sigma) + 1;
        kWidth = 2 * floor(5 * sigma) + 1;
        img_height = src.rows;
        img_width = src.cols;
        if (img_height < kHeight || img_width < kWidth) {
            cout << "卷积核大小超过图像大小！" << endl;
            return 0;
        }
    }

    // 初始化高斯卷积核
    kernel = Mat::ones(kHeight, kWidth, CV_32F);

    // 找到高斯核的中心点
    // 注意该中心点是以0开头，10σ结尾的中心点
    int center = floor(5 * sigma);

    // 遍历Mat，求值
    for (int i = 0; i < kHeight; i++) {
        for (int j = 0; j < kWidth; j++) {
            // 坐标（i，j）对应的高斯坐标系中的坐标为(i - center, center - j)
            double x = i - center;
            double y = center - j;
            kernel.at<float>(i, j) = 1.0f / (2.0f * pi*sigma*sigma)*exp(-(1.0f)* ((x * x + y * y) / (2.0f*sigma*sigma)));
            cout << kernel.at<float>(i, j) << "\t\t";
        }
        cout << endl;
    }

    Point anchor(-1, -1); //中间的点
    int depth = -1;//深度和输入一样
    int delta = 0; //在处理之后　再加上delta,默认0

    filter2D(src, dst, depth, kernel, anchor, delta);
    imshow("高斯滤波", dst);
    imwrite(output_name, dst);
    waitKey(0);
}