NFA转化为DFA
NFA（不确定的有穷自动机）转化为DFA（确定的有穷自动机）
NFA转换DFA，通常是将带空串的NFA（即：ε-NFA）先转化为不带空串的NFA（即：NFA），然后再转化为DFA。
提示：ε是空串的意思！空串没有任何字符！
这里直接讲将ε-NFA转化为DFA的过程，将NFA转化为DFA的情况类似。
转化的过程总的来说有两大步骤：ε-NFA转化为DFA，以及DFA简化
ε-NFA转化为DFA前件知识
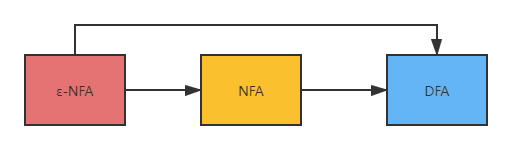
1、对状态图进行改造
增加状态X，Y，使之成为新的唯一的初态和终态，从X引ε弧到原初态节点，从原终态节点引ε弧到Y节点。
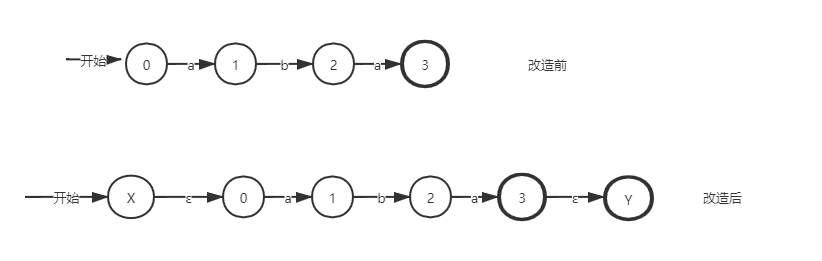
2、利用子集法对NFA进行确定化。
- 子集法
子集法：将NFA转化为接受同样语言的DFA。
DFA的每一个状态对应NFA的一组状态；
DFA使用它的状态去记录NFA读入一个符号后可能达到的所有状态
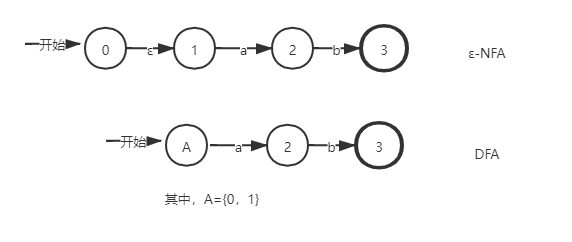
如上图，A对应ε-NFA的0和1状态，A代表的是一组状态。因此，DFA使用它的状态去记录NFA读入一个符号后可能达到的所有状态。
- 构造状态转化表
- ε-closure（ε-闭包）
状态集合I的ε-闭包是一状态集。
①任何状态q∈I，则q∈ε-closure(I)
②任何状态q∈I，则q经任意条ε弧而能到达的状态q'∈ε-closure(I)
比如上图，假设I={0}，那么0∈ε-closure(I);并且0经ε弧能到达1状态，因此，1∈ε-closure(I)。即：ε-closure({0})={0,1}。
案例再现
可能前面的理论有些乱，理不清，这里用一个例题演绎如何将ε-NFA转化为DFA。
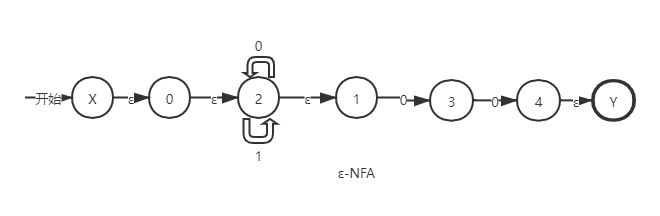
已知下面的NFA图，求确定后的DFA：
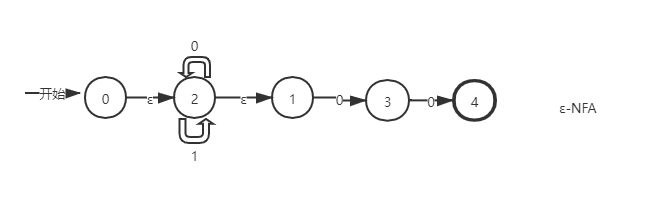
①改造状态图:在起始状态分别加上X、Y状态，连接输入符号为ε。
②状态转换表
| 状态集合 \状态 | 0 | 1 |
|---|---|---|
| A= | B={2，3，1} | C= |
| B= | D= | C= |
| C= | B= | C= |
| D= | D= | C= |
！提示：A,B,C,D表示状态集合；0，1分别表示状态0和1。第二行第二列表示状态集合A的状态在输入符号0后到达的状态的ε-闭包为B={2，3，1}。
获得改造后的状态图后，我们找到起始状态为X，由于X与0之间是输入的ε符号，所以X与0等价；同理，0与2等价，1与2等价。所以，起始状态有{X,0,2,1}，我们给它命名为状态A。
再看第二列，处于起始状态A时，当输入字符为0时到达的状态分别有：2输入0到达2本身；1输入0到达3，因此还有3状态。再看与2等价的状态有：1；与3等价的状态无。因此，输入字符0时到达的状态有{2，3}，它的闭包是：{2，3，1}。
第三列同理，处于起始状态A时，当输入字符为1时到达的状态只有2。2的等价状态有1。因此，输入字符1时A到达的状态有{2}，它的闭包是{2，1}。
！注意：状态转换表里面填入的是闭包结果。
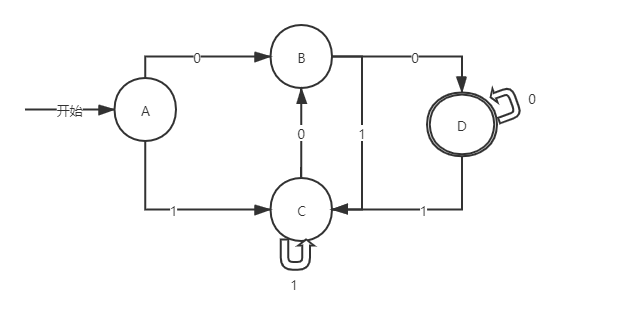
最后得到的DFA图为：(未简化)
DFA简化
状态S和状态T等价的条件
- 一致性条件：状态S和T必须同时为可接受状态或不可接受状态。
- 蔓延性条件：对于所有符号，状态S和T必须转换到等价的状态里。
DFA简化算法：
1、假定一个集合中的状态都是等价的，首先将DFA的所有状态放在一个集合I中。
2、所有状态分成两个子集——终态集和非终态集。运用判定状态等价原则分别对两个子集的状态进行分析和划分。若发现某个状态与其他状态不等价，则将其作为一个新的状态子集，如果无法区分，则放在同一子集中。
3、从每个子集中选出一个状态做代表，即可构成简化的DFA。
4、含有原来初态的子集仍为初态，各终态的子集仍为终态。
案例再现
将上面未简化的DFA图简化：
①I = {A,B,C,D}
②拆分终态集和非终态集：
非终态集{A,B,C}+终态集{D}
③对{A,B,C}继续拆分：
A输入0后到达B，而B⊆{A,B,C}，故A不能拆分；
再看B，B输入0后到达D，而D￠，故B可以拆分；
再看C，C输入0后到达B，B⊆{A,B,C}，故C也不能拆分。
综上：{A,B,C}可拆分为{A,C}+{B}。
④对{A，C}继续拆分：
A输入1时到达C，而C⊆{A,C}，故A不可拆分；
再看C，C输入1时到达C状态，而C⊆{A,C}，故C也不可拆分。
⑤综合起来，上面未简化的DFA图简化后得到的状态应该是：{A,C}+{B}+{D}。
！注意：同一个{}大括号里面的状态是等价的，因此，画图时选其一即可。
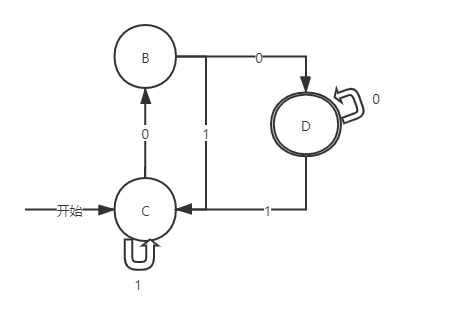
简化后的DFA图为：
Are you got it?(你学会了吗？)
