返回一个整数数组中最大子数组的和

题目：返回一个整数数组中最大子数组的和

要求：1，输入一个整形数组，数组里有正数也有负数。

           2 ，数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

           3，如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]，……A[n-1]，A[j-1]之和最大。

           4，同时返回最大子数组的位置。

           5，求所有子数组的和的最大值。

设计思想：在上课时，经过老师的提示，再加上自己下课分析，总结思路如下：对于一个数组，如果首位相连，那么我们可以把它当成一个环状，若想求最大子数组的和，必须把它剪开，这样就可以把复杂的                     问题转换成一个简单的数组求最大子数组的和，剪开后，若原来数组共n个子数，那么剪开后有n种结果，在其中一种可能中寻找最大子数组的和，找到后记录首末位子数位置，再将首尾换位置，子                   数位 置不变，遍历整个数组直到再找到一个最大子数组，例如第一次找到的末尾是第n个位置，那么下次就遍历第一个元素，因此环状数组不同于链状数组的地方就在于链状中是最大就是最大，而                     环状的数  组还要考虑首尾相接的地方。

实验代码：

#include<iostream>

#define n 100

using namespace std;
void main()
{
    int a[n], b[n][n];
    int length, i, j, w = 0, p = 0, q = 0, temp, m;
    cout << "输入随机整数" << endl;
    for (length = 0;;)
    {
        cin >> a[length];
        length++;
        if (getchar() == '\n')
        {
            break;
        }
    }
    cout << "这个数组的长度为：" << length << endl;
    //求子数组
    for (i = 0; i<length; i++)//两次循环，进行排除法，判断每个数所构成的最大子数组
    {
        m = i;
        w = 0;
        j = 0;
        while (j <= length - 1)
        {
            w += a[m];
            b[i][j] = w;
            m++;
            if (m>length - 1)
            {
                m = 0;
            }
            j++;
        }
    }
 
    temp = b[0][0];
    for (i = 0; i<length; i++)//将每个数对应的最大子数组进行判断，最后得到整个整数组的最大子数组
    {
        for (j = 0; j<length; j++)
        {
            if (b[i][j]>temp)
            {
                temp = b[i][j];
                p = i;
                q = j;
            }
        }
    }
 
    cout << "最大子数组的值为：" << temp << endl;
    cout << "最大子数组中元素的下标位子置：" << endl;
    i = 0;
    while (i <= q)
    {
        cout << p << "  ";
        p++;
        if (p >= length)
        {
            p = 0;
        }
        i++;
    }
 
    cout << endl;
}

测试结果：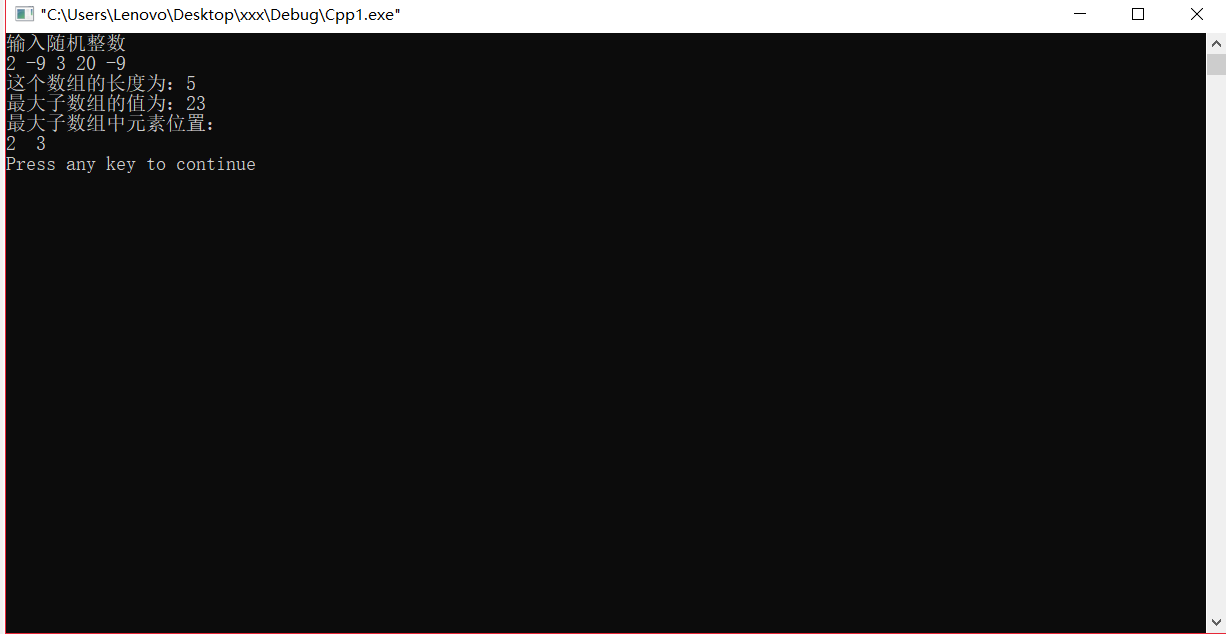

实验成员：常啸帆（负责分析代码，代码编程），毕文强（负责代码复审和代码测试）

总结：编程就像老师说的那样，如果我们把一件大事情分割成若干小事情，做好每件小事情最终把他们用一定的规则连接起来，就可以解决问题。