Matplotlib从兴趣到实践

先看下Matplotlib实现的效果

是不是出现了也想敲一个的心动，那让我们一起来了解Matplotlib吧

Matplotlib安装##

1.Windows系统安装Matplotlib
进入到cmd的命令界面，输入以下命令：
python -m pip install -U pip setuptools
python -m pip install matplotlibm

2.Linux系统安装Matplotlib

• Ubuntu: sudo apt-get install python-matplotlib
• Redhat: sudo yum install python-matplotlib

Mac OSX 系统安装 Matplotlib
可以使用 pip 命令来安装：sudo python -mpip install matplotlib

图文显示##

首先我们需要下载中文包：ShiHei字体包 将下载的字体包放置到项目目录中

import matplotlib
import numpy as np
from matplotlib import pyplot as plt

zhfont1 = matplotlib.font_manager.FontProperties(fname="SimHei.ttf")
x=np.array([1,2,3,4,5,6,7,8])
y = 2 * x + 5
plt.title("我的 - 测试", fontproperties=zhfont1)

fontproperties 设置中文显示，fontsize 设置字体大小
plt.xlabel("x 轴", fontproperties=zhfont1)
plt.ylabel("y 轴", fontproperties=zhfont1)
plt.plot(x, y,"-b")
plt.show()

执行结果：

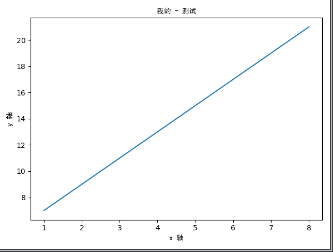
从执行结果来看不难分析出pil.xlable实现的是定义x轴的默认显示，ylabel定义的是y轴的显示 ，plot(x,y,'-b')中定义的是x y轴的数据以及显示的颜色和样式信息。
其中具体的样式和颜色信息的设置参数如下

字符	plot函数中字符描述
'-'	实线样式
'--'	短横线样式
'-.'	点划线样式
':'	虚线样式
'.'	点标记
','	像素标记
'o'	圆标记
'v'	倒三角标记
'^'	正三角标记
'<'	左三角标记
'>'	右三角标记
'1'	下箭头标记
'2'	上箭头标记
'3'	左箭头标记
'4'	右箭头标记
's'	正方形标记
'p'	五边形标记
'*'	星形标记
'h'	六边形标记 1
'H'	六边形标记 2
'+'	加号标记
'x'	X 标记
'D'	菱形标记
'd'	窄菱形标记
'|'	竖直线标记
'_'	水平线标记

字符	plot函数中颜色描述
'b'	蓝色
'g'	绿色
'r'	红色
'c'	青色
'm'	品红色
'y'	黄色
'k'	黑色
'w'	白色

下面我们可以运用Numpy的相关知识绘制各种图像##

我们的目的重点不是编写各种的图像，而是了解绘图的原理，通过学习能够绘制符合自己需要的图像（学习matplotlib前建议要学习Numpy的知识）

绘制正弦波###

#计算正弦曲线上点的 x 和 y 坐标
x = np.arange(0,  3  * np.pi,  0.1) 
y = np.sin(x)
plt.title("sine wave form")  
#使用 matplotlib 来绘制点
plt.plot(x, y) 
plt.show()

运行结果：

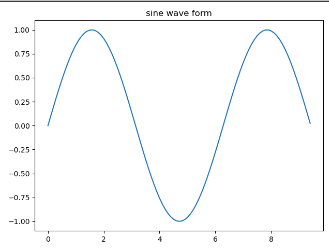
该代码中 x是一个数组，它是借助numpy.arange()方法实现0-（3*圆周率）的范围内每间隔0.1生成一个点
y = np.sin(x)
表示的是运用正弦函数生成与x轴点一 一对应的y轴的点，最后使用matplotlib的plot方法绘制出来相应的图像。

绘制同一窗口中不同的图像###

实现多个图像的绘制就要用的matplotlib的subplot（）函数

#subplot参数解释 以下创建的是一个高度为2，宽度为1，的第1个图像
plt.subplot(2, 1, 1)
#将第一个图像绘制出来
plt.plot(x,y_sin)
plt.title('Sin')
#subplot参数解释 以下创建的是一个高度为2，宽度为1，的第2个图像
plt.subplot(2, 1, 2)
#将第二个图像绘制出来
plt.plot(x,y_cos)
plt.title('Cos')
plt.show()

运行结果：

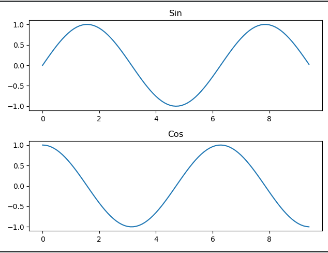
绘制条形图###

绘制条形图需要用到matplotlib的bar()函数生成条形图，使用原理与上面的图像绘制一样，不同的是方法产生的效果
可以通过以下代码来进一步加深图像绘制的印象

# 条形图 bar
x = [5,8,10]
y = [12,16,6]
x2 = [6,9,11]
y2 = [6,15,7]
plt.bar(x, y, align='center')
plt.bar(x2, y2, color='y', align='center')
plt.title('条形图', fontproperties=zhfont1)
plt.ylabel('Y 轴', fontproperties=zhfont1)
plt.xlabel('X 轴', fontproperties=zhfont1)
plt.show()

运行结果：

绘制直方图###

hist()函数可以将将数据和bin参数作为参数，并且能够转化为直方图

# 直方图 plt()
a = np.array([21,99,1,46,88,77,15,24,11,61,66,67,68,30,41,55,18,31,90,26])
plt.hist(a, color='g', bins=[0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
plt.title("histogram")
plt.show()

运行结果：

扩展##

关于matplotlib绘图的常用配置说明

# 导入 matplotlib 的所有内容（nympy 可以用 np 这个名字来使用）
from pylab import *

# 创建一个 8 * 6 点（point）的图，并设置分辨率为 80
figure(figsize=(8,6), dpi=80)

# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
subplot(1,1,1)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

# 绘制余弦曲线，使用蓝色的、连续的、宽度为 1 （像素）的线条
plot(X, C, color="blue", linewidth=1.0, linestyle="-")

# 绘制正弦曲线，使用绿色的、连续的、宽度为 1 （像素）的线条
plot(X, S, color="green", linewidth=1.0, linestyle="-")

# 设置横轴的上下限
xlim(-4.0,4.0)  /plt.xlim(X.min()*1.1, X.max()*1.1)

# 设置横轴记号
xticks(np.linspace(-4,4,9,endpoint=True))

# 设置纵轴的上下限
ylim(-1.0,1.0)

# 设置纵轴记号
yticks(np.linspace(-1,1,5,endpoint=True))

#添加图例 可以指定图例的位置
plt.legend(loc='upper left', frameon=False)

# 以分辨率 72 来保存图片
# savefig("exercice_2.png",dpi=72)

# 在屏幕上显示
show()

下面是一个综合运用的实例

# 绘制正弦波
# 计算正弦曲线上点的 x 和 y 坐标
x = np.linspace(-np.pi, np.pi, 256,endpoint=True)
y = np.sin(x)
C,S = np.cos(x), np.sin(x)
plt.title("sine wave form")
# 使用 matplotlib 来绘制点
plt.plot(x, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plt.plot(x, S, color="red", linewidth=2.5, linestyle="-", label="sine")
#以下是对边界的设置
plt.xlim(x.min()*1.1, x.max()*1.1)
#以下是对x轴的记号设置
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
           [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
#以下是对y轴的记号设置
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, +1],
           [r'$-1$', r'$+1$'])
#以下是对label图例位置进行设置
plt.legend(loc='upper left', frameon=False)
plt.show()

运行结果：

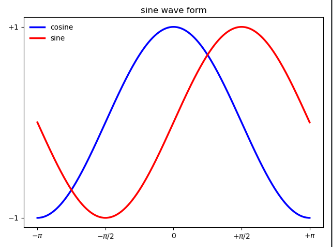
下面一个是使用matplotlib中的pie()函数实现的饼状图的实例：

n = 20
Z = np.random.uniform(0,1,n)
plt.pie(Z) 
plt.show()

运行结果：

也可以用来实现一些3D的图像效果，下面是一个实现的实例：

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot')
plt.savefig('sample.png', bbox_inches="tight")
show()

运行结果：

是不是