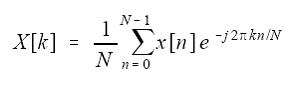傅里叶变换

傅里叶变化(FTT)：

主要思想：任何连续周期信号可以由一组适当的正弦曲线(函数)或者它们的积分组合而成

正弦信号特征：输入输出保持不变 可当做信号的特征向量

 

对应频域图：

频域：

幅度和相位：幅度-分量的幅度 角度是波的相对相位

频域图：横轴频率 纵轴幅度 描述了信号的频率结构及频率与该频率信号幅度的关系。

 

短时傅里叶变换(STFT)

利用窗函数在时间范围上对信号进行切分

不同时间范围内对应不同窗函数

窗函数有不同类型(余弦函数：汉明窗，指数窗：高斯窗等)

 

 

 

确定时变信号局部区域正弦波的频率和相位

计算多个时刻的频谱图（在时间上切分对局部进行傅里叶变换）

具有时间分辨率和频率分辨率两个条件

在信号变动剧烈时，需要时间分辨率较高(切分时间间隔较短)，对应频率分辨率较低

信号变动平缓时，需要时间分辨率较低(切分时间间隔较长)，对应频率分辨率较高

 

相关知识：

1.一个长度为N的信号可以分解为N/2+1个正余弦信号

  (最多只能有这些不同频率，再多超出计算机的精度范围)

2.时域到频域的转换

 

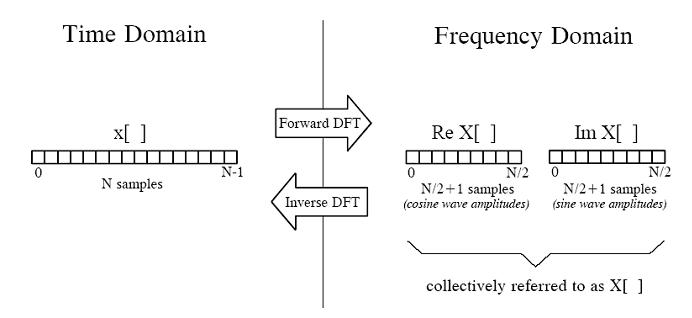
正逆变换

有N/2+1种频率，所以数组长度为N/2+1，复数形式的变换长度是N

2.频域中频率表示方法：

1）序号：0~N/2

2）分数：时域中信号样本数的比例 0~0.5：X[f]，f=k/N,范围0-1/2

3）弧度值：f*2π得到一个弧度值，自然频率表示方法:X[w]，w=2πf=2πk/N,取值范围0-π

4）赫兹：Hz 10kHz代表每秒10000个样本数 范围0~取样频率的一半

3.实数离散傅里叶变换(DFT)

ck[i] = cos(2πki/N)
sk[i] = sin(2πki/N)

k表示每个正余弦波的频率，如为2表示在0到N长度中存在两个完整的周期

合成原始信号(real实部 lmagine虚部)：

 

 

 

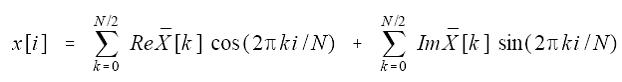
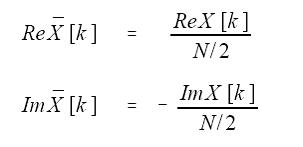
k=0 or N/2时，实数部分用到下面等式

 

 

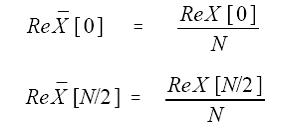
N是时域中点的总数，k是从0到N/2的序号。

 

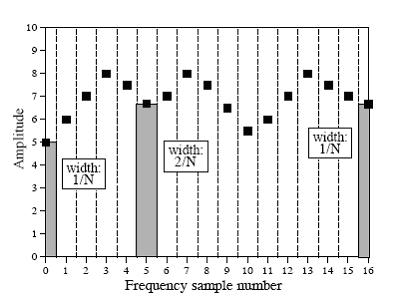
 信号相关性(correlation)：

 可以从噪声背景中检测已知信号，比如把一个待检测的信号波乘以另一个已知信号波，得到一个新的信号波，把新的

信号波所有点数相加(y)，得到平均值，就可以判断两个信号相似程度，0为不相似。0.5为包含。

（两个函数相乘，结果中每个点的总和为0，认为这两个函数是正交函数）

把输入信号和每一种频率的正余弦信号相乘，就可以得到原始信号和每种频率的关联程度，就是需要的傅里叶变换结果。

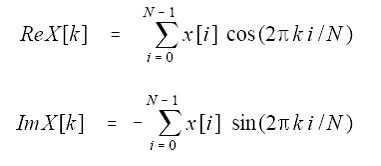
 复数相关知识：

M(magnitude)数量积，表示从原点到坐标点的距离

θ是相位角（phase），表示x轴到某个方向的夹角

 

计算方法如下：

 

 

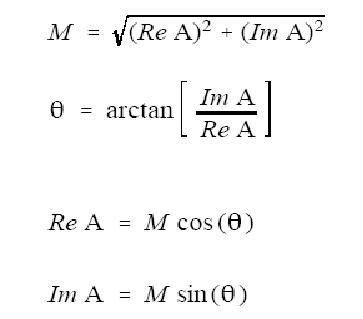
 直角坐标到极坐标转换：

 a + jb = M (cosθ + j sinθ)

直角坐标表示：

 

 

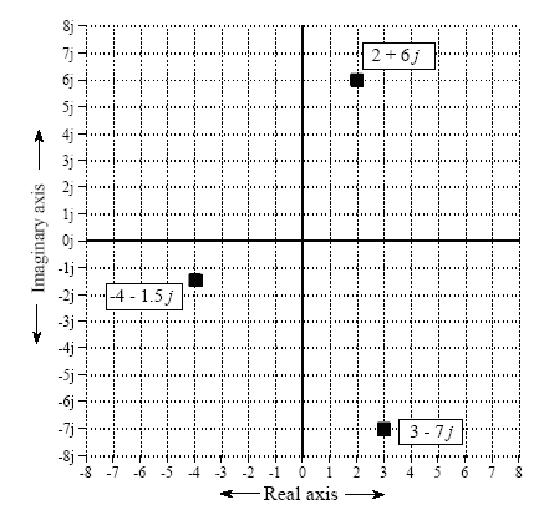
 极坐标表示：

 

 

 

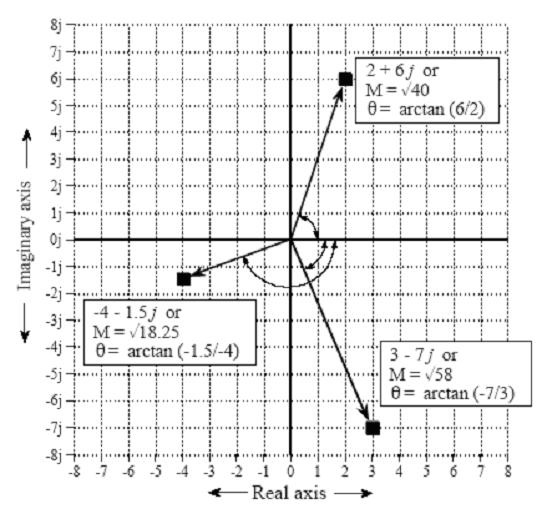
利用欧拉等式

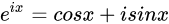(i：虚部)

 

 

得到

 

 

 

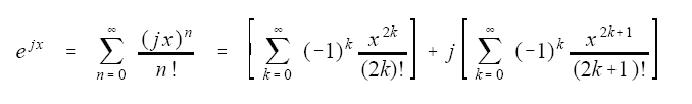
得到 a + jb = M ejθ （这便是复数的两个表达式）

 

 

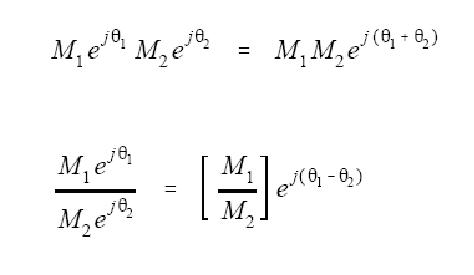
 正余弦复数形式运算条件：

1、参加运算的所有正余弦的频率必须是一样的；

2、运算操作必须是线性的，如两个正弦信号可以进行相加减，但不能进行乘除，象信号的放大、衰减、高低通滤波等系统都是线性的，象平方、缩短、取限等则不是线性的。要记住的是卷积和傅立叶分析也只有线性操作才可以进行。
   

相量变换：

正弦或余弦波变成复数的形式称为相量变换，Phasor transform

 

 

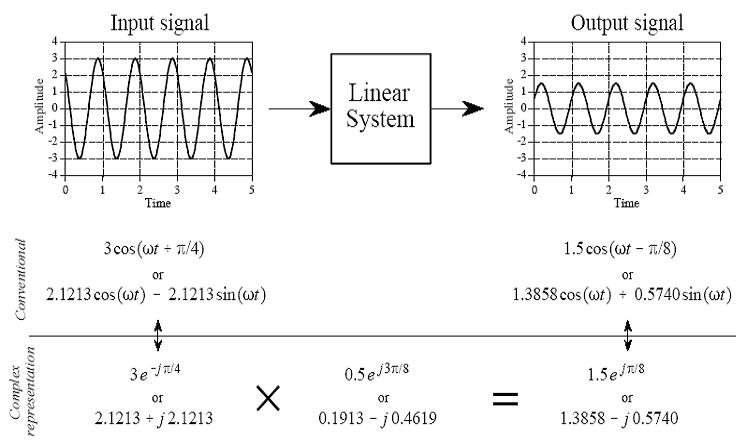
离散傅里叶变换复数形式：

通过欧拉等式可以把正余弦函数表示成复数的形式：
 
                    cos( x ) = 1/2 e j(-x) + 1/2 ejx 
                    sin( x ) = j (1/2 e j(-x) - 1/2 ejx)

 复数形式可以包含正负频率。

 原始信号乘以一个正交函数形式的信号，然后进行求总和，最后就能得到这个原始信号所包含的正交函数信号的分量。

 

正向变换式：

 

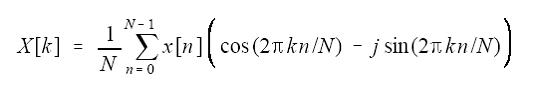
欧拉变换：