【学习笔记】莫队
【学习笔记】莫队
普通莫队
形式
假设 \(n=m\),那么对于序列上的区间询问问题,如果从 \([l,r]\) 的答案能够 \(O(1)\) 扩展到 \([l-1,r],[l+1,r],[l,r+1],[l,r-1]\)(即与 \([l,r]\) 相邻的区间)的答案,那么可以在 \(O(n \sqrt{n})\) 的复杂度内求出所有询问的答案。
解释
离线后排序,顺序处理每个询问,暴力从上一个区间的答案转移到下一个区间答案(一步一步移动即可)。
排序方法
对于区间 \(l,r\) , 以所 \(l\) 在块的编号为第一关键字, \(r\) 为第二关键字从小到大排序。
例题
优化 \(1\) :重新赋编号,数据可能相同值比较集中,所以加上这个优化直接从 44pts 变成 84pts。
优化 \(2\) :区间移动的代价不要写成函数 add 和 del,用 bool 压一下行,巨快。96pts。
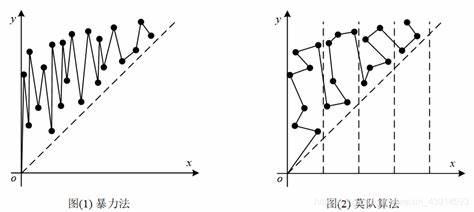
优化 \(3\) :奇偶性排序。因为根据莫队排序后点对 \((l, r)\) 的分布大概长这样(如右图),但我们可以继续优化:奇数块按 \(r\) 递增,偶数块按 \(r\) 递减,这样横坐标在块内移动的代价是 \(O(\sqrt{n})\),但纵坐标不会出现忽上忽下的情况。这个优化有通用性而且优化巨大。100pts。
#include<bits/stdc++.h>
#define F(i,l,r) for(int i(l);i<=(r);++i)
#define G(i,r,l) for(int i(r);i>=(l);--i)
using namespace std;
using ll = long long;
char buf[100], *p1 = buf, *p2 = buf, obuf[80000000], *o = obuf;
inline int gc(){
return (p1 == p2) && (p2 = (p1 = buf) + fread(buf, 1, 100, stdin), p1 == p2) ? EOF : *p1 ++;
}
inline int rd(){
int x = 0; char ch;
while(!isdigit(ch = gc()));
do x = (x << 3) + (x << 1) + (ch ^ 48); while(isdigit(ch = gc()));
return x;
}
inline void write(int x){
if(x > 9) write(x / 10);
*o++=(x % 10 + 48);
}
const int N = 1e6 + 5;
int cnt[N], a[N], from[N], ans[N];
int n, m, nw = 0, block, sum = 0;
struct node{
int id, l, r;
bool operator < (const node &o)const{
int ls = (l - 1) / block + 1, rs = (o.l - 1) / block + 1;
return (ls == rs) ? ((ls & 1) ? r < o.r : r > o.r) : ls < rs;
}
}q[N];
signed main(){
n = rd();
F(i, 1, n){
a[i] = rd();
if(!from[a[i]]) from[a[i]] = ++ nw;
a[i] = from[a[i]];
}
m = rd();
F(i, 1, m) q[i].id = i, q[i].l = rd(), q[i].r = rd();
block = m / __builtin_sqrt(n);
sort(q + 1, q + m + 1);
int L, R, l = 1, r = 0;
F(i, 1, m){
L = q[i].l, R = q[i].r;
while(l > L) sum += !(bool) cnt[a[-- l]] ++;
while(r < R) sum += !(bool) cnt[a[++ r]] ++;
while(l < L) sum -= !(bool) -- cnt[a[l ++]];
while(r > R) sum -= !(bool) -- cnt[a[r --]];
ans[q[i].id] = sum;
}
F(i, 1, m) write(ans[i]), *o++='\n';
return fwrite(obuf, o - obuf, 1, stdout), fflush(0), 0;
}
参考博客:

