矩阵【基础算法题】

题目一

 

 思路：

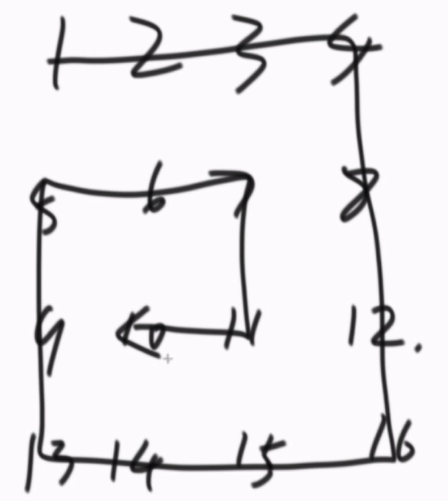
①得到二维数组左上角(a,b)和右下角(c,d)的点，就能打印出最外层的框。

如果，得到的左上角(a,b)和右下角(c,d)是在同一行，即a=c，说明该数组是棒状结构，直接从(a,b)加到(a,d)即可。

如果，得到的左上角(a,b)和右下角(c,d)是在同一列，即b=d，说明该数组是棒状结构，直接从(a,b)加到(c,b)即可。

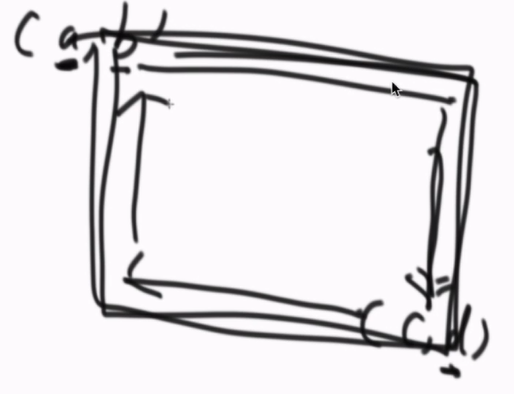
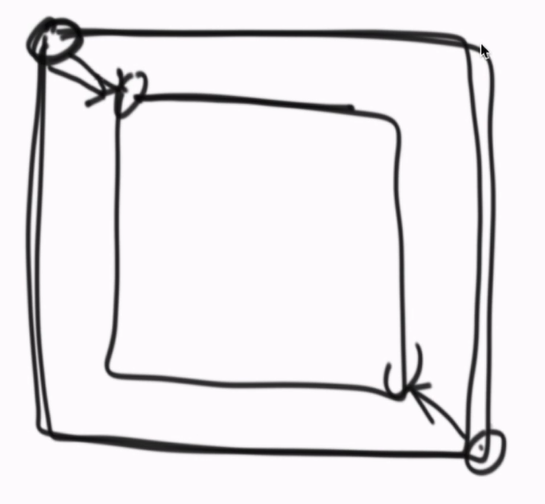
 ②最外层框打完之后，左下角和右下角的点，同时往对角线方向走一个点，再打印里面一层的框，···以此类推，直到左下角的行或列大于右下角的行或列就可以停了。

 

 代码实现

package class_03;

public class Code_06_PrintMatrixSpiralOrder {

    public static void spiralOrderPrint(int[][] matrix) {
        int tR = 0;//左下角的行
        int tC = 0;//左下角的列
        int dR = matrix.length - 1;//右下角的行
        int dC = matrix[0].length - 1;//右下角的列
        while (tR <= dR && tC <= dC) {//左下角没有越过右下角，就说明还有数可以打印
            printEdge(matrix, tR++, tC++, dR--, dC--);
        }
    }

    public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
        if (tR == dR) {//左下角和右下角在同一行
            for (int i = tC; i <= dC; i++) {
                System.out.print(m[tR][i] + " ");
            }
        } else if (tC == dC) {//左下角和右下角在同一列
            for (int i = tR; i <= dR; i++) {
                System.out.print(m[i][tC] + " ");
            }
        } else {
            int curC = tC;
            int curR = tR;
            while (curC != dC) {
                System.out.print(m[tR][curC] + " ");
                curC++;
            }
            while (curR != dR) {
                System.out.print(m[curR][dC] + " ");
                curR++;
            }
            while (curC != tC) {
                System.out.print(m[dR][curC] + " ");
                curC--;
            }
            while (curR != tR) {
                System.out.print(m[curR][tC] + " ");
                curR--;
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                { 13, 14, 15, 16 } };
        spiralOrderPrint(matrix);

    }

}

题目二

 

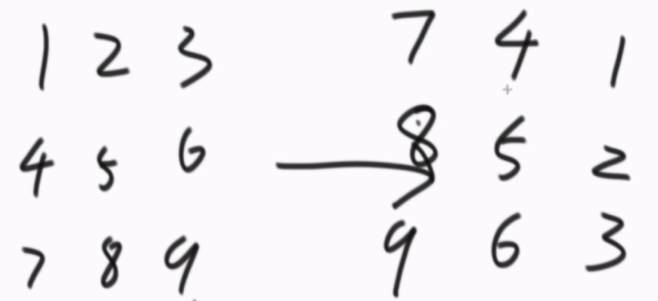
 思路

同样，得到矩阵的左上角和右下角，先转外圈的，再转内圈的，···以此类推，直到把框转没，最终就全部转了90度了。

外层为例：

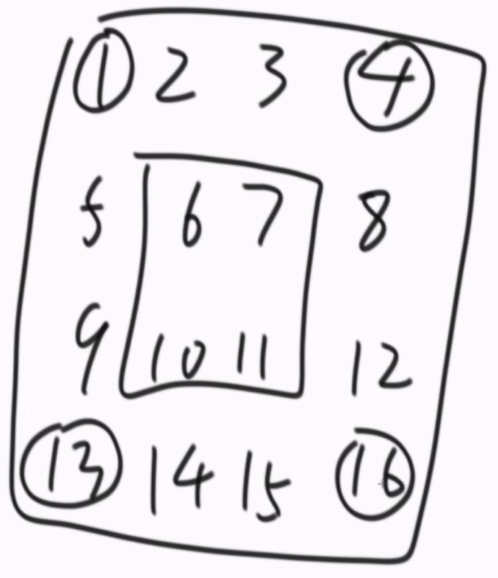
首先1、4、16、13，这四个点先交换位置，1→4、4→16、16→13、13→1；

接着2、8、15、9，这四个点交换位置，2→8、8→15、15→9、9→2；

接着3、12、14、5，这四个点交换位置，3→12、12→14、14→5、5→3；

····内层以此类推

 代码实现

package class_03;

public class Code_05_RotateMatrix {

    public static void rotate(int[][] matrix) {
        int tR = 0;
        int tC = 0;
        int dR = matrix.length - 1;
        int dC = matrix[0].length - 1;
        while (tR < dR) {
            rotateEdge(matrix, tR++, tC++, dR--, dC--);
        }
    }

    public static void rotateEdge(int[][] m, int tR, int tC, int dR, int dC) {
        int times = dC - tC; 
        int tmp = 0;
        for (int i = 0; i != times; i++) {
            tmp = m[tR][tC + i];
            m[tR][tC + i] = m[dR - i][tC];
            m[dR - i][tC] = m[dR][dC - i];
            m[dR][dC - i] = m[tR + i][dC];
            m[tR + i][dC] = tmp;
        }
    }

    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i != matrix.length; i++) {
            for (int j = 0; j != matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                { 13, 14, 15, 16 } };
        printMatrix(matrix);
        rotate(matrix);
        System.out.println("=========");
        printMatrix(matrix);

    }

}

题目三

 

 思路

设置A、B两个点，一开始都在(0,0)位置。每次A跟B都同时各自走一步

 A总是向右移动，撞到最右了，往下移动；

B总是向下移动，撞到最右了，往右移动；

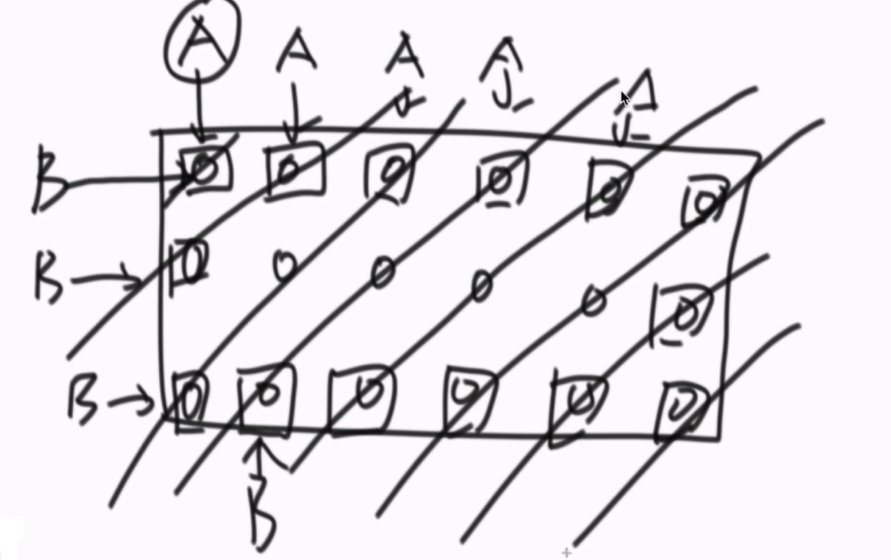
最终题目就转换为，已知一条对角线的右上点和左下点 ，怎么打印这条对角线？解决了这个问题，就可以依次打印每条对角线，首先打印第一个点(0,0)，然后开始打印对角线上的数，第一条从右上往左下打印，第二条从左下往右上打印，（可以设置一个布尔值来记录打印的方向是左上还是右下）···以此类推，直到打印完最后一条对角线上的数，最后打印整个矩阵右下角的数，就实现了题目的要求。

代码实现

package class_03;

public class Code_08_ZigZagPrintMatrix {

    public static void printMatrixZigZag(int[][] matrix) {
        int tR = 0;
        int tC = 0;
        int dR = 0;
        int dC = 0;
        int endR = matrix.length - 1;
        int endC = matrix[0].length - 1;
        boolean fromUp = false;
        while (tR != endR + 1) {
            printLevel(matrix, tR, tC, dR, dC, fromUp);
            tR = tC == endC ? tR + 1 : tR;
            tC = tC == endC ? tC : tC + 1;
            dC = dR == endR ? dC + 1 : dC;
            dR = dR == endR ? dR : dR + 1;
            fromUp = !fromUp;
        }
        System.out.println();
    }

    public static void printLevel(int[][] m, int tR, int tC, int dR, int dC,
            boolean f) {
        if (f) {
            while (tR != dR + 1) {
                System.out.print(m[tR++][tC--] + " ");
            }
        } else {
            while (dR != tR - 1) {
                System.out.print(m[dR--][dC++] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
        printMatrixZigZag(matrix);

    }

}

题目四

 思路

从右上角开始找，如果当前位置上的数比要找的数大，就往左走，如果当前位置上的数比要找的数小，就往下走，···以此类推，直到找到返回true，如果走到左下角还是没有就返回false。

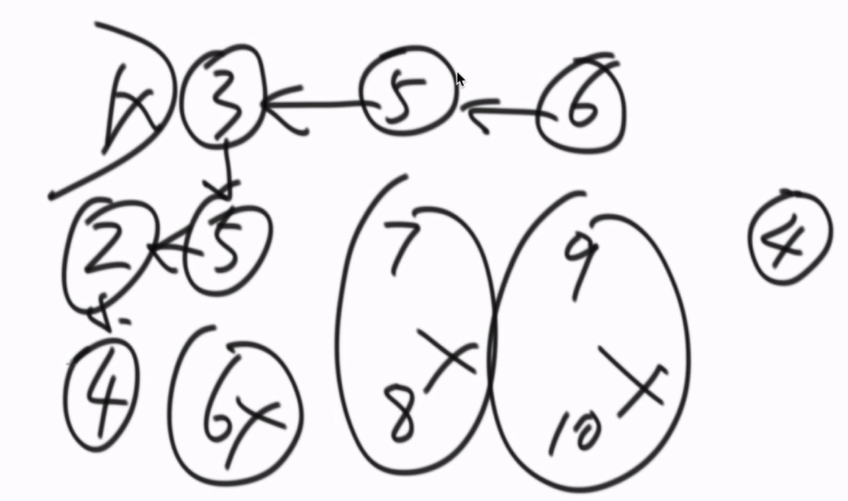复杂度O(n+m)

总结

题目给出的数据状况很特殊或问法特殊的话，就从这个特殊的数据状况上或问法上来着手，往往能够找到最优解。

代码实现

package class_03;

public class Code_09_FindNumInSortedMatrix {

    public static boolean isContains(int[][] matrix, int K) {
        int row = 0;
        int col = matrix[0].length - 1;
        while (row < matrix.length && col > -1) {
            if (matrix[row][col] == K) {
                return true;
            } else if (matrix[row][col] > K) {
                col--;
            } else {
                row++;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = new int[][] { { 0, 1, 2, 3, 4, 5, 6 },// 0
                { 10, 12, 13, 15, 16, 17, 18 },// 1
                { 23, 24, 25, 26, 27, 28, 29 },// 2
                { 44, 45, 46, 47, 48, 49, 50 },// 3
                { 65, 66, 67, 68, 69, 70, 71 },// 4
                { 96, 97, 98, 99, 100, 111, 122 },// 5
                { 166, 176, 186, 187, 190, 195, 200 },// 6
                { 233, 243, 321, 341, 356, 370, 380 } // 7
        };
        int K = 233;
        System.out.println(isContains(matrix, K));
    }

}