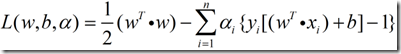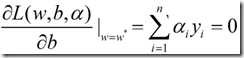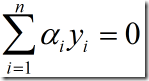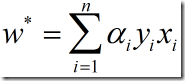支持向量机（3）

    第二篇主要是讲述了SVM中最简单的情况，也就是线性可分的两类问题。在前面给出的公式中，对Lagrange函数的产生过程及接下来的推导还是有一些疑问，后来查了一些资料，终于释放掉心中的疑云，现记录如下。

    有疑问的地方是：

    前文说的最优分类面问题转化成如下的约束优化问题，即在条件

        的约束下，求函数

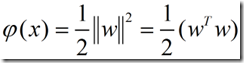    的最小值。这是没问题的，但是紧接着作者通过定义一个Lagrange函数将整个问题转化成了另一个极值问题。那么我们先来看看何为Lagrange乘子法。

    Lagrange乘子法：

    其实在上学的时候肯定学过Lagrange乘子法，但说实话现在的印象已经很朦胧了。通过查阅wiki和《模式识别》，加深了对它的了解。

    Lagrange乘子法是一种在等式约束条件下的优化算法。它将一个有n个变量与k个约束条件的最优化问题转化为一个有n+k个变量的方程组的极值问题，其变量不受任何约束。同时它引入了一个标量未知数--Lagrange乘子 。

    一个简单的例子就是：

    最大化

    受限于

    引入新变量拉格朗日乘数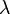，即可求解下列拉格朗日方程

         接下来主要就是通过使偏导的值为0来求出参数。

仿照上面的式子，我们就可以写出自己的Lagrange函数：

             （1）

接下来进行推导1。

    将（1）式对w和b求偏导，

                 （2）

                 （3）

由（2），（3）可得

               其中    （4）

              （5）

    将（5）和（4）代入（1），有：

       

    这样，运算过程基本上就清晰了。