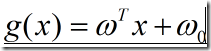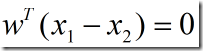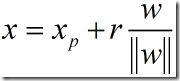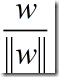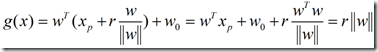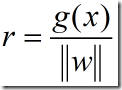支持向量机系列（1）

    上学的时候，在《模式识别》课程里面接触到支持向量机，但说实话，那时候对它一知半解。虽然当时完成了一个大作业，效果也不错，但终究对它有一种似是而非的感觉。为了不让这种感觉再继续下去，这段时间好好研究一下。接下来会用几篇日志记载这段时间的收获。

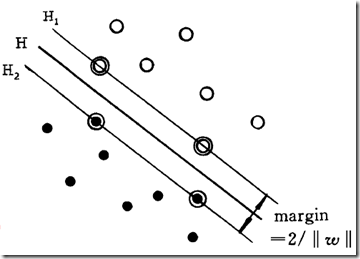
    要学习支持向量机，先从我教材《模式识别》（边肇祺，张学工版）出发。这次看书的时候对书上297页的一个地方，也就是最优分类面：

       

 

的分类间隔是 具体怎么推导出来有点不明白，书上的推导过程是放在4.1节即“线性判别函数”那一节。现在来看看具体的推导过程：

    给出两类情况下判别函数为线性的一般表达式：

            （1）

        式中x是d维特征向量，又称样本向量，w称为权向量， 是阈值权。则可以采用下面的决策规则：

    令

    

如果

       （2）

    方程g(x)实际上定义了一个决策面，将归类为 的点与归类为 的点分割开来。如果g(x)为线性函数，则这个决策面是超平面。假设 和 都是决策面上的点，则有：

             或      （3）

这表明w和超平面上任意向量正交，即w垂直于超平面。

    判别函数g(x)可以看成是特征空间中某点x到超平面的距离的一种代数度量。

    把x表示成：

           （4）

式中， 是x在H上的投影向量

    r是x到H的垂直距离

        是w方向上的单位向量。

    其实上面的式子就是把一个向量做正交分解，这个我们在高中物理中就学过了，因而这一块是没有问题的。

    将（4）式代入（1）式，可得到：

           或写作

               （5）

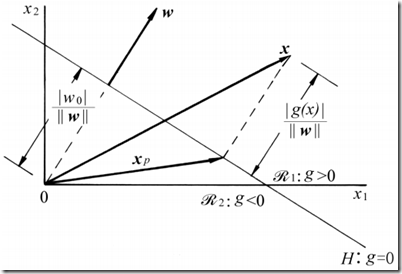
示意图如下图所示：

       

        其实让我有疑问的是公式（5）中的那一长串，原因是我被上面这张图误导了。这张图让我产生了一种错觉，让我以为 是垂直于 向量，那么就应该有。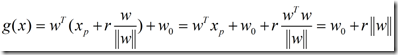

    结果我推来推去老得到超平面经过原点的结论。后来经过仔细阅读书上的文字，突然醒悟。原来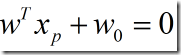 是一个很直观的结论，因为 是x在超平面上的投影，那么就意味着 在超平面上，而超平面上的点必须满足（1）式等于0。 其实，只要将上图中那条斜线看成一个平面，这样的错误就不会产生了，因为这时候能很明显的感觉到 跟超平面是有夹角的。

    一旦把这一关打通，后面就好理解了。

    后记：有时候人一旦陷入一个思维怪圈，就很难走出来。其实看明白之后，会发现自己在纠结一个最简单的问题，但如果没反应过来，那它就越来越复杂。生活中很多事情都是如此。