数据结构与算法-07树及二叉树

树

树（Tree）是一种非线性数据结构，它由若干个节点（Node）和若干个边（Edge）组成，节点之间的关系是一对多的关系。树的一个节点称为父节点（Parent Node），它的直接子节点称为子节点（Child Node），没有子节点的节点称为叶子节点（Leaf Node）。

树的一个重要特点是从根节点（Root Node）到任意节点都有唯一的一条路径。树的深度（Depth）是从根节点到叶子节点的最长路径长度，树的高度（Height）是从根节点到叶子节点的最短路径长度。

树可以用来表示层次关系，例如文件系统、组织结构、HTML文档等。树还可以用来实现搜索、排序、编译等算法。

树有很多种不同的形态，例如二叉树、平衡树、B树、红黑树等。其中二叉树是最简单、最基础的树形结构，它的每个节点最多有两个子节点，分别称为左子节点和右子节点。

树的常见应用场景

xml/html解析
路由协议
mysql数据库索引
文件系统结构

二叉树

二叉树（Binary Tree）是一种特殊的树形结构，它的每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的子树也是二叉树。

二叉树有很多种不同的形态，例如满二叉树、完全二叉树、平衡二叉树等。其中满二叉树是一种特殊的二叉树，它的每个节点都有两个子节点，除了叶子节点外没有空缺节点。完全二叉树是一种二叉树，它的最后一层节点可以不满，但是所有节点都集中在左侧。平衡二叉树是一种二叉树，它的左子树和右子树的高度差不超过1。

二叉树可以用来实现搜索、排序、编译等算法。二叉树的遍历有三种方式：前序遍历、中序遍历和后序遍历。前序遍历是先访问根节点，然后访问左子树，最后访问右子树。中序遍历是先访问左子树，然后访问根节点，最后访问右子树。后序遍历是先访问左子树，然后访问右子树，最后访问根节点。

二叉树的特点

在二叉树的第i层上至多有2^(i-1)个结点
深度为k的二叉树至多有2^k-1个结点
对于任意一颗二叉树, 如果其叶结点数为N, 则度数为2的节点总数为N+1
具有n个节点的完全二叉树的深度必为log2(n+1)
对于完全二叉树, i节点的左孩子变化为2i, 右孩子为2i+1

二叉树的分类

满二叉树（Full Binary Tree）：每个节点都有两个子节点，除了叶子节点外没有空缺节点（每一层都满了）。
完全二叉树（Complete Binary Tree）：最后一层节点可以不满，但是所有节点都集中在左侧（除了最下层,每一层都满了）。
平衡二叉树（Balanced Binary Tree）：左子树和右子树的高度差不超过1（任意两个节点的高度差不大于1）。
二叉搜索树（Binary Search Tree）：左子树的所有节点的值都小于根节点的值，右子树的所有节点的值都大于根节点的值。
红黑树（Red-Black Tree）：一种自平衡的二叉搜索树，保证了树的高度不超过2log(n+1)。
B树（B-Tree）：一种多路搜索树，每个节点可以有多个子节点，用于磁盘和数据库等应用。
Trie树（Trie Tree）：一种前缀树，用于字符串的匹配和搜索。
Huffman树（Huffman Tree）：一种用于数据压缩的树形结构，将出现频率高的字符编码为短的二进制码。

二叉树的实现

以下是Python实现一个二叉树的示例代码：
节点

class Node(object):
    def __init__(self, item):
        self.elem = item
        self.lchild = lchild
        self.rchild = rchild

树

class BinaryTree(object):
    def __init__(self, root=None):
        self.root = root
        
    def add(self, item):
        node = Node(item)
        if self.root is None
            self.root = node
            return
        else:
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)

二叉树遍历

根据先序遍历+中序遍历或后序+中序推导出一颗树

先从先序/后序中找出root节点
在中序中找到root节点分成两半
先序中安装中序中的两半分开
左右子树分别重复前三步操作

class BinaryTree(object):
    # ...
    # 广度优先遍历
    def breadth_travel(self):
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queuq.pop(0)
            print(cur_node.elem)
            if cur_node.lchild is not None:
                quequ.append(cur_node.lchild)
            if cur_node.rchild is not None:
                queue.append(rchild)
    # 先序遍历
    def preorder(self, node):
        if node is None:
            return
        print(node.elem)
        self.preorder(node.lchild)
        self.preorder(node.rchild)
        
    # 中序遍历
    def inorder(self, node):
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.elem)
        self.inorder(node.rchild)
        
    # 后序遍历
    def postorder(self, node):
        if node is None:
            return
        self.postorder(node.lchild)
        self.postorder(node.rchild)
        print(self.elem)

红黑树

红黑树（Red-Black Tree）是一种自平衡的二叉搜索树，它保证了树的高度不超过2log(n+1)，其中n是树中节点的数量。红黑树的每个节点都有一个颜色，可以是红色或黑色。红黑树满足以下性质：

每个节点要么是红色，要么是黑色。
根节点是黑色的。
每个叶子节点（NIL节点）是黑色的。
如果一个节点是红色的，则它的两个子节点都是黑色的。

对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

红黑树的插入和删除操作都会改变树的结构，因此需要进行自平衡操作，以保证树的高度不超过2log(n+1)。红黑树的自平衡操作包括左旋、右旋、变色等操作，这些操作可以保证树的性质不被破坏。

红黑树的时间复杂度比普通的二叉搜索树更稳定，插入、删除和查找操作的时间复杂度均为O(log n)。红黑树广泛应用于C++ STL中的map和set等容器，以及Java中的TreeMap和TreeSet等容器。

以下是Python实现一个红黑树的示例代码：

RED = True
BLACK = False

class Node:
    def __init__(self, key, value, color=RED):
        self.key = key
        self.value = value
        self.color = color
        self.left = None
        self.right = None

class RedBlackTree:
    def __init__(self):
        self.root = None

    def is_red(self, node):
        if node == None:
            return False
        return node.color == RED

def rotate_left(self, node):
    x = node.right
    node.right = x.left
    x.left = node
    x.color = node.color
    node.color = RED
    return x

def rotate_right(self, node):
    x = node.left
    node.left = x.right
    x.right = node
    x.color = node.color
    node.color = RED
    return x

def flip_colors(self, node):
    node.color = RED
    node.left.color = BLACK
    node.right.color = BLACK

def insert(self, key, value):
    self.root = self._insert(self.root, key, value)
    self.root.color = BLACK

def _insert(self, node, key, value):
    if node == None:
        return Node(key, value)
    if key < node.key:
        node.left = self._insert(node.left, key, value)
    elif key > node.key:
        node.right = self._insert(node.right, key, value)
    else:
        node.value = value

    if self.is_red(node.right) and not self.is_red(node.left):
        node = self.rotate_left(node)
    if self.is_red(node.left) and self.is_red(node.left.left):
        node = self.rotate_right(node)
    if self.is_red(node.left) and self.is_red(node.right):
        self.flip_colors(node)

    return node

def search(self, key):
    node = self.root
    while node != None:
        if key == node.key:
            return node.value
        elif key < node.key:
            node = node.left
        else:
            node = node.right
    return None

def delete(self, key):
    self.root = self._delete(self.root, key)

def _delete(self, node, key):
    if node == None:
        return None
    if key < node.key:
        node.left = self._delete(node.left, key)
    elif key > node.key:
        node.right = self._delete(node.right, key)
    else:
        if node.left == None:
            return node.right
        elif node.right == None:
            return node.left
        else:
            min_node = self._min(node.right)
            node.key = min_node.key
            node.value = min_node.value
            node.right = self._delete(node.right, min_node.key)

    if self.is_red(node.right) and not self.is_red(node.left):
        node = self.rotate_left(node)
    if self.is_red(node.left) and self.is_red(node.left.left):
        node = self.rotate_right(node)
    if self.is_red(node.left) and self.is_red(node.right):
        self.flip_colors(node)

    return node

def _min(self, node):
    while node.left != None:
        node = node.left
    return node

这个红黑树使用Node类来表示树中的节点，每个节点包括键、值、颜色、左子节点和右子节点。红黑树支持插入、查找和删除操作，其中插入和删除操作会改变树的结构，需要进行自平衡操作。红黑树的自平衡操作包括左旋、右旋、变色等操作，这些操作可以保证树的性质不被破坏。红黑树的时间复杂度比普通的二叉搜索树更稳定，插入、删除和查找操作的时间复杂度均为O(log n)。你可以根据自己的需求对这个示例代码进行修改和扩展。

B+树

B+树是一种多路搜索树，它是B树的一种变体，常用于数据库和文件系统中。B+树的特点是：
B+树

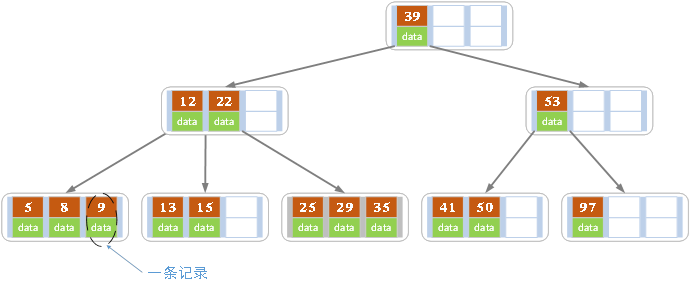
所有数据都存储在叶子节点中，非叶子节点只存储索引信息。
所有叶子节点都按照顺序连接成一个链表，便于范围查询。
非叶子节点的子节点数目可以大于2，通常为M路，其中M为一个固定的正整数。
所有叶子节点的深度相同，可以通过非叶子节点的指针快速定位。

B+树的插入和删除操作与B树类似，也需要进行节点分裂和合并等操作，以保持树的平衡。B+树的查找操作也与B树类似，从根节点开始逐层搜索，直到找到目标节点或者到达叶子节点。B+树的时间复杂度与B树类似，插入、删除和查找操作的时间复杂度均为O(log n)。

B+树的优点：

叶子节点的顺序连接可以提高范围查询的效率。
非叶子节点的子节点数目可以大于2，可以减少树的高度，提高查找效率。
所有数据都存储在叶子节点中，可以减少磁盘I/O操作，提高数据访问效率。

B+树广泛应用于数据库和文件系统中，例如MySQL、Oracle、MongoDB等数据库系统，以及Linux文件系统中的Ext4、XFS等。以下是Python实现一个B+树的示例代码：

class Node:
    def __init__(self, is_leaf=False):
        self.keys = []
        self.values = []
        self.children = []
        self.is_leaf = is_leaf

    def is_full(self):
        return len(self.keys) == M - 1

class BPlusTree:
    def __init__(self):
        self.root = Node(is_leaf=True)

    def search(self, key):
        node = self.root
        while not node.is_leaf:
            i = bisect_left(node.keys, key)
            if i < len(node.keys) and node.keys[i] == key:
                return node.values[i]
            node = node.children[i]
        i = bisect_left(node.keys, key)
        if i < len(node.keys) and node.keys[i] == key:
            return node.values[i]
        return None

    def insert(self, key, value):
        node = self.root
        path = []
        while not node.is_leaf:
            i = bisect_left(node.keys, key)
            path.append((node, i))
            node = node.children[i]
        i = bisect_left(node.keys, key)
        node.keys.insert(i, key)
        node.values.insert(i, value)
        if node.is_full():
            self._split(node, path)

    def _split(self, node, path):
        parent = None
        while path:
            node, i = path.pop()
            if not node.is_full():
                return
            new_node = Node(is_leaf=node.is_leaf)
            mid = len(node.keys) // 2
            new_node.keys = node.keys[mid:]
            new_node.values = node.values[mid:]
            node.keys = node.keys[:mid]
            node.values = node.values[:mid]
            if not node.is_leaf:
                new_node.children = node.children[mid:]
                node.children = node.children[:mid]
            i = bisect_left(parent.keys, new_node.keys[0]) if parent else 0
            parent.keys.insert(i, new_node.keys[0])
            parent.children.insert(i+1, new_node)
            node = parent
            parent = path.pop()[0] if path else None
        if not parent:
            parent = Node()
            parent.keys = [node.keys[0]]
            parent.children = [node, new_node]
            self.root = parent
        else:
            i = bisect_left(parent.keys, new_node.keys[0])
            parent.keys.insert(i, new_node.keys[0])
            parent.children.insert(i+1, new_node)

    def delete(self, key):
        node = self.root
        path = []
        while not node.is_leaf:
            i = bisect_left(node.keys, key)
            path.append((node, i))
            node = node.children[i]
        i = bisect_left(node.keys, key)
        if i < len(node.keys) and node.keys[i] == key:
            node.keys.pop(i)
            node.values.pop(i)
            if node.is_leaf:
                self._delete_leaf(node, path)
            else:
                self._delete_internal(node, path)
        else:
            return

    def _delete_leaf(self, node, path):
        while len(node.keys) < M // 2 and path:
            parent, i = path.pop()
            if i == len(parent.children) - 1:
                sibling = parent.children[i-1]
                if len(sibling.keys) > M // 2:
                    node.keys.insert(0, sibling.keys.pop())
                    node.values.insert(0, sibling.values.pop())
                    parent.keys[i-1] = sibling.keys[-1]
                    break
                else:
                    sibling.keys.extend(node.keys)
                    sibling.values.extend(node.values)
                    sibling.children.extend(node.children)
                    node = sibling
            else:
                sibling = parent.children[i+1]
                if len(sibling.keys) > M // 2:
                    node.keys.append(sibling.keys.pop(0))
                    node.values.append(sibling.values.pop(0))
                    parent.keys[i] = sibling.keys[0]
                    break
                else:
                    node.keys.extend(sibling.keys)
                    node.values.extend(sibling.values)
                    node.children.extend(sibling.children)
                    parent.keys.pop(i)
                    parent.children.pop(i+1)
                    node = parent
        if not node.keys and path:
            parent, i = path.pop()
            parent.children.pop(i)
            if len(parent.children) < M // 2 and path:
                self._delete_internal(parent, path)

def _delete_internal(self, node, path):
    while len(node.keys) < M // 2 and path:
        parent, i = path.pop()
        if i == len(parent.children) - 1:
            sibling = parent.children[i-1]
            if len(sibling.keys) > M // 2:
                node.keys.insert(0, parent.keys[i-1])
                parent.keys[i-1] = sibling.keys.pop()
                node.children.insert(0, sibling.children.pop())
                break
            else:
                sibling.keys.append(parent.keys.pop(i-1))
                sibling.keys.extend(node.keys)
                sibling.children.extend(node.children)
                node = sibling
        else:
            sibling = parent.children[i+1]
            if len(sibling.keys) > M // 2:
                node.keys.append(parent.keys[i])
                parent.keys[i] = sibling.keys.pop(0)
                node.children.append(sibling.children.pop(0))
                break
            else:
                sibling.keys.insert(0, parent.keys.pop(i))
                sibling.keys[:0] = node.keys
                sibling.children[:0] = node.children
                node = sibling
    if not node.keys and path:
        parent, i = path.pop()
        parent.children.pop(i)
        if len(parent.children) < M // 2 and path:
            self._delete_internal(parent, path)

这个B+树使用Node类来表示树中的节点，每个节点包括键、值、子节点和是否为叶子节点等信息。B+树支持插入、查找和删除操作，其中插入和删除操作会改变树的结构，需要进行节点分裂和合并等操作

posted @ 2023-06-07 18:51 韩志超阅读(85) 评论(0) 编辑收藏举报

刷新页面返回顶部

...

临渊