数据结构与算法-03链表

链表

链表是一种线性表，它使用一组通过指针相互连接的节点来存储元素。每个节点包含一个数据元素和一个指向下一个节点的指针。链表的元素在内存中不必连续存储，因此可以动态地增加或删除元素，而不需要移动其他元素。

链表分为单向链表、双向链表和循环链表等多种类型。单向链表每个节点只有一个指针，指向下一个节点；双向链表每个节点有两个指针，分别指向前一个节点和后一个节点；循环链表的最后一个节点指向第一个节点，形成一个环。

链表的优点是插入和删除操作比较快，适合于元素数量频繁变化的场景。缺点是访问效率比较低，因为需要遍历整个链表才能访问指定位置的元素。另外，链表需要额外的存储空间来存储指针，因此占用的内存比顺序表更大。

链表通常使用指针来实现，指针指向下一个节点或者前一个节点。链表的头节点是一个特殊的节点，它不包含数据元素，只包含指向第一个节点的指针。链表的尾节点的指针通常为空，表示链表的结束。

一个节点分为两部分,数据区和链接区, 链接区指向下一个节点

单项链表

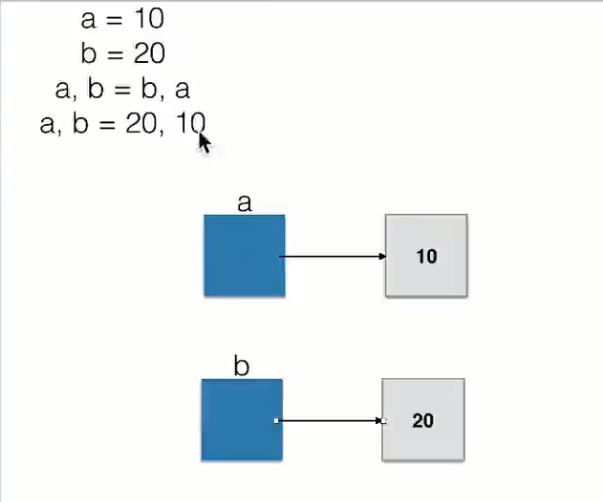
a, b = b, a的本质
python中变量是一块单独的空间, 其中保存的是所代表对象的地址

单项链表的实现

"""单项链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class SingleLinkList(object):
    def __init__(self, node=None):
        self.__head = node

    def add(self, item):
        node = Node(item)
        if self.__head:
            self.__head, node.next = node, self.__head
        else:
            self.__head = node

    def append(self, item):
        node = Node(item)
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        else:
            self.__head = node
        
    def travel(self):
        if self.__head:
            cur = self.__head
            while cur is not None:
                print(cur.elem)
                cur = cur.next

    def remove(self, item):
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                if cur.next.elem == item:
                    cur.next = cur.next.next
                    break
                cur = cur.next
            else:
                print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item):
        i = 0
        cur = self.__head
        if pos == 0:
            self.add(item)
        elif pos + 1 > self.length:
            raise ValueError
        else:
            while cur.next is not None:
                i += 1
                if i == pos:
                    new_node = Node(item)
                    cur.next, new_node.next = new_node, cur.next
                    break
                elif i > pos:
                    raise ValueError
                cur = cur.next

    def search(self, item):
        if self.__head:
            cur = self.__head
            while cur is not None:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next

    @property
    def length(self):
        count = 0
        if self.__head:
            cur = self.__head
            while cur is not None:
                count += 1
                cur = cur.next
        return count

    def is_empty(self):
        return self.__head is None

循环链表

循环链表是一种链表，它的最后一个节点指向第一个节点，形成一个环。循环链表可以从任意一个节点开始遍历，因此比单向链表和双向链表更加灵活。

循环链表的节点通常包含两个部分：数据元素和指向下一个节点的指针。循环链表的头节点可以是任意一个节点，因为从任意一个节点开始遍历都可以遍历整个链表。

循环链表的插入和删除操作与单向链表和双向链表类似，但是需要特别处理最后一个节点指向第一个节点的情况。循环链表的访问效率与单向链表和双向链表类似，但是需要特别处理从最后一个节点到第一个节点的情况。

循环链表的实现

"""循环链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class CircleLinkList(object):
    def __init__(self, node=None):
        if node is None:
            self._head = None
        else:
            self._head = node.next = node

    def add(self, item):
        node = Node(item)
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur
            node.next, self._head = self._head, node
            last.next = self._head
        else:
            self._head = node.next = node

    def append(self, item):
        node = Node(item)
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur
            last.next, node.next = node, self._head
        else:
            self._head = node.next = node
        
    def travel(self):
        if self._head:
            cur = self._head
            while cur.next != self._head:
                print(cur.elem, end=" ")
                cur = cur.next
            print(cur.elem)

    def remove(self, item):   # 单节点remove
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur

            cur = self._head
            if cur.elem == item:
                self._head = last.next = cur.next
            else:
                while cur.next != self._head:
                    if cur.next.elem == item:
                        cur.next = cur.next.next
                        break
                    cur = cur.next 
                else:
                    print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item): 
        length = self.length
        if pos == 0:
            self.add(item)
        elif pos == length:
            self.append(item)
        elif pos > length:
            raise ValueError
        else:
            i = 0
            cur = self._head
            while cur.next != self._head :
                i += 1
                if i == pos:
                    node = Node(item)
                    cur.next, node.next = node, cur.next
                    break
                cur = cur.next

    def search(self, item):
        if self._head:
            cur = self._head
            while cur.next != self._head:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next
            else:
                if cur.elem == item:
                    print(cur.elem)

    @property
    def length(self):
        count = 0
        if self._head:
            cur = self._head
            while cur.next != self._head:
                count += 1
                cur = cur.next
            count += 1
        return count

    def is_empty(self):
        return self._head is None

if __name__ == '__main__':
    s = CircleLinkList()
    s.append(0)
    s.append(1)
    s.append(2)
    s.append(3)
    s.remove(0)
    s.insert(3, 4)
    s.search(1)
    s.travel()

双向链表

双向链表是一种链表，每个节点包含两个指针，一个指向前一个节点，一个指向后一个节点。双向链表可以从前往后遍历，也可以从后往前遍历，因此比单向链表更加灵活。

双向链表的节点通常包含三个部分：数据元素、指向前一个节点的指针和指向后一个节点的指针。双向链表的头节点和尾节点的指针通常为空，表示链表的开始和结束。

双向链表的插入和删除操作比较方便，因为可以通过前一个节点和后一个节点的指针来修改节点的连接关系。双向链表的访问效率比单向链表高，因为可以从前往后或者从后往前遍历，但是双向链表需要额外的存储空间来存储前一个节点的指针，因此占用的内存比单向链表更大。

双向链表的实现

"""双项链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.pre = None
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class DoubleLinkList(object):
    def __init__(self, node=None):
        self.__head = node

    def add(self, item):
        node = Node(item)
        if self.__head:
            self.__head, self.__head.pre, node.next = node, node, self.__head
        else:
            self.__head = node

    def append(self, item):
        node = Node(item)
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            cur.next, node.pre = node, cur
        else:
            self.__head = node
        
    def travel(self):
        if self.__head:
            cur = self.__head
            while cur is not None:
                print(cur.elem, end=" ")
                cur = cur.next

    def remove(self, item):
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                if cur.next.elem == item:
                    cur.next, cur.next.next.pre = cur.next.next, cur
                    break
                cur = cur.next
            else:
                print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item):
        i = 0
        cur = self.__head
        if pos == 0:
            self.add(item)
        elif pos + 1 > self.length:
            raise ValueError
        else:
            while cur.next is not None:
                i += 1
                if i == pos:
                    new_node = Node(item)
                    cur.next, new_node.next, new_node.pre = new_node, cur.next, cur
                    break
                elif i > pos:
                    raise ValueError
                cur = cur.next

    def search(self, item):
        if self.__head:
            cur = self.__head
            while cur is not None:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next

    @property
    def length(self):
        count = 0
        if self.__head:
            cur = self.__head
            while cur is not None:
                count += 1
                cur = cur.next
        return count

    def is_empty(self):
        return self.__head is None

跳表

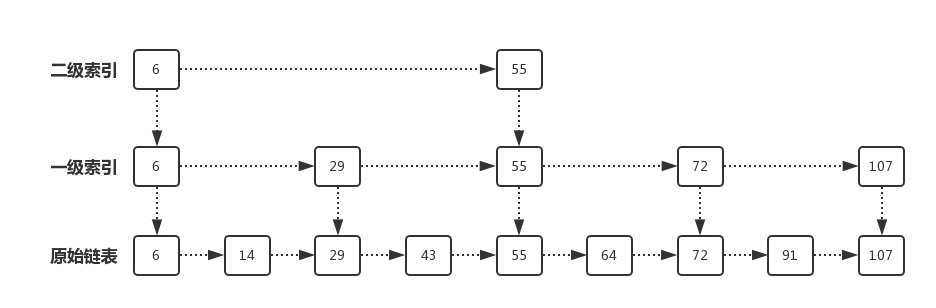
跳表（Skip List）是一种基于链表的数据结构，用于快速查找有序链表中的元素。

跳表的特点

• 跳表中的元素按照升序排列。
• 跳表中的每个节点包含多个指针，可以跨越多个节点进行快速查找。
• 跳表中的每个节点包含一个随机数，用于决定该节点的指针数量。

跳表的查找操作与二分查找类似，从顶层开始逐层查找，直到找到目标元素或者到达底层。跳表的插入和删除操作也与链表类似，需要进行节点的插入和删除操作，同时需要更新节点的指针信息，以保持跳表的平衡。跳表的时间复杂度与平衡树类似，插入、删除和查找操作的时间复杂度均为O(log n)。

跳表的优点：

• 跳表的实现简单，易于理解和实现。
• 跳表的插入、删除和查找操作的时间复杂度均为O(log n)，与平衡树类似。
• 跳表的空间复杂度较低，只需要额外存储每个节点的指针信息。

跳表广泛应用于Redis等内存数据库中，以及一些高性能的网络库中，例如Nginx等。以下是Python实现一个跳表的示例代码：

import random

class Node:
    def __init__(self, key=None, value=None, level=0):
        self.key = key
        self.value = value
        self.forward = [None] * (level + 1)

class SkipList:
    def __init__(self):
        self.head = Node()
        self.level = 0

    def search(self, key):
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].key < key:
                node = node.forward[i]
        node = node.forward[0]
        if node and node.key == key:
             return node.value
        return None

    def insert(self, key, value):
        update = [None] * (self.level + 1)
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].key < key:
                node = node.forward[i]
            update[i] = node
        node = node.forward[0]
        if node and node.key == key:
            node.value = value
        else:
            level = self._random_level()
            if level > self.level:
                for i in range(self.level + 1, level + 1):
                    update[i] = self.head
                self.level = level
            node = Node(key, value, level)
            for i in range(level + 1):
                node.forward[i] = update[i].forward[i]
                update[i].forward[i] = node
    
    def delete(self, key):
        update = [None] * (self.level + 1)
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].key < key:
                node = node.forward[i]
            update[i] = node
        node = node.forward[0]
        if node and node.key == key:
            for i in range(self.level + 1):
                if update[i].forward[i] != node:
                    break
                update[i].forward[i] = node.forward[i]
            while self.level > 0 and not self.head.forward[self.level]:
                self.level -= 1
    
    def _random_level(self):
        level = 0
        while random.random() < 0.5 and level < 16:
            level += 1
        return level

在这个示例代码中，跳表使用Node类来表示节点，每个节点包括键、值和多个指针信息。跳表支持查找、插入和删除操作，其中插入和删除操作需要进行节点的插入和删除操作，同时需要更新节点的指针信息，以保持跳表的平衡。跳表的时间复杂度与平衡树类似，插入、删除和查找操作的时间复杂度均为O(log n)。