面向对象第一单元总结
面向对象第一单元总结
前言
由于在三次作业中本人以基于重构的方式历次实现的,存储数据的原理在第一次到第二次有了质的改变;解析表达式的方法也在第二次到第三次有了突变。最终第三次实现了一种比较合理的解析、运算与存储结构,因此下面的分析将以第三次为主,前两次为辅。
一、度量分析
程序实现与架构
主类:
MainClass负责读入数据,并做最初步的处理,将初步优化的字符串传递给下属类解析。最后进行输出。
数据保管:
Factor类为一个抽象因子类,其中保存了因子的指数exp(常数的exp为其本身),并有get/set/derive等基础方法;Cos/Sin/Const/power/Poly五个类继承了Factor类,并根据自己特殊需要重写、增加了一些方法;Item类为因子类,保存着一个ArrayList型的factor容器,和系数base;Expression为表达式类,保存着一个ArrayList型的item容器。
运算:
MulDerive类实现对项求导并返回表达式。
化简:
所有的化简都在ToSimplify中实现,包括在一个项中对因子实现乘法合并;在一个表达式中对项实现减加法合并;三角函数优化等等。
类图
根据每次作业类与类之间的关系,我大致梳理总结了各次作业的类图
第一次作业
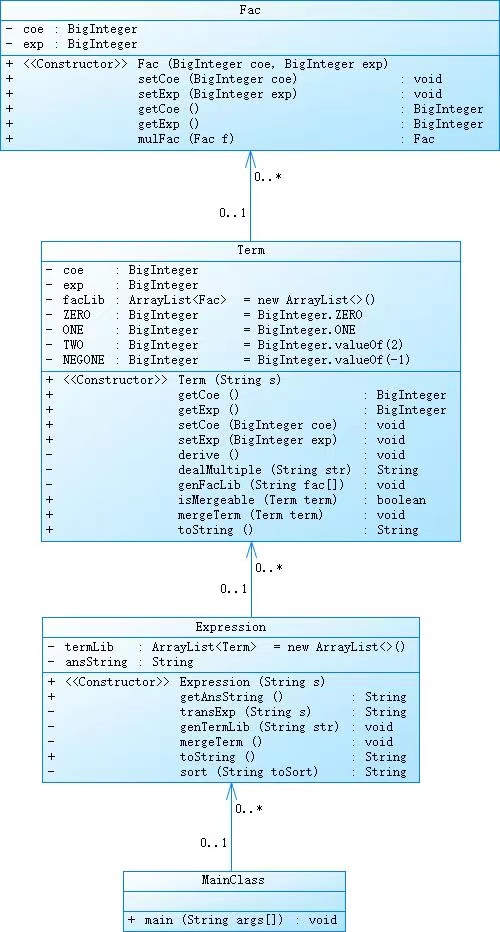
可以看到,第一次作业的耦合性还是很高的。
第二次作业
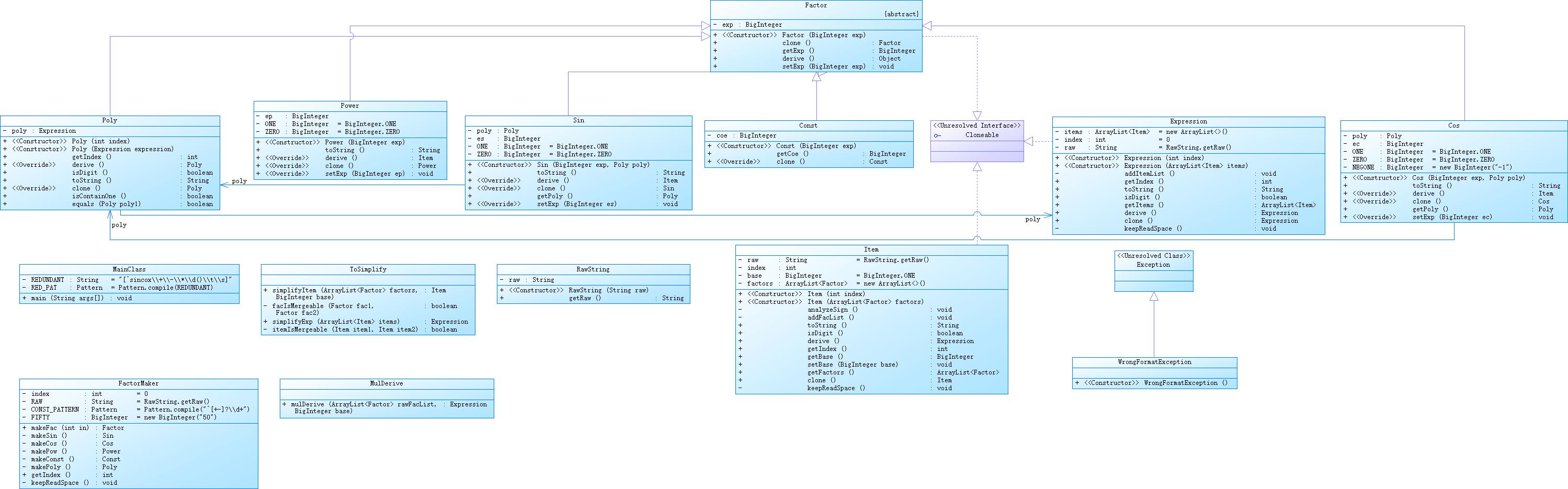
第三次作业
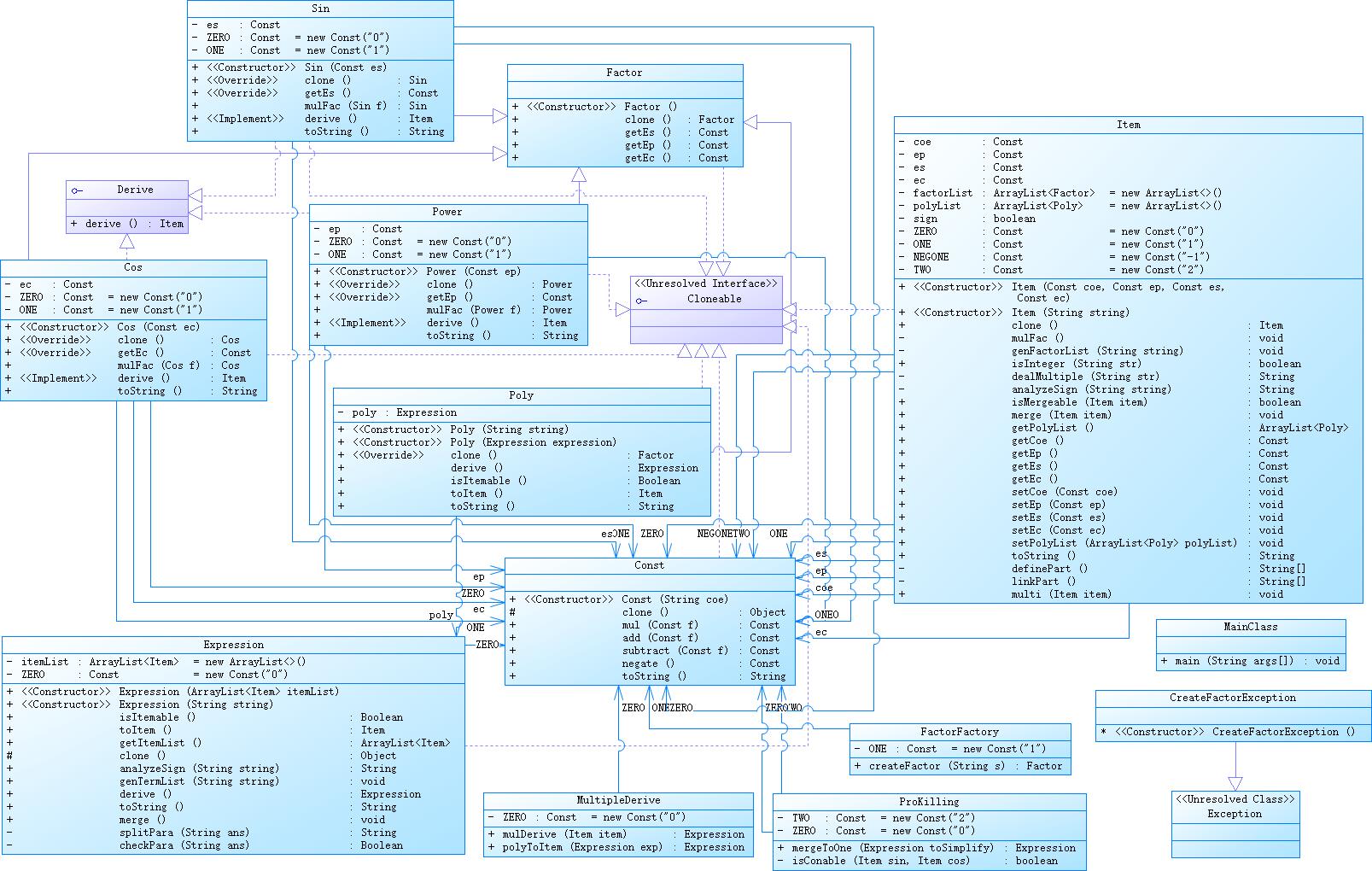
度量分析
对方法的度量分析
下表展示了程序中每个方法的度量分析,首先做一下表内名词解释
ev(G):基本复杂度,用于衡量程序的非结构化程度,基本复杂度高意味着非结构化程度高,难以模块化和维护。
iv(G):模块设计复杂度,用来衡量模块判定结构,即模块和其他模块的调用关系。该值高意味着耦合度高,难以隔离、维护。
v(G):圈复杂度,用来衡量一个模块判定结构的复杂程度,即合理的预防错误所需测试的最少路径条数。
第一次作业
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Term.toString() | 14.0 | 11.0 | 6.0 | 15.0 |
| Term.Term(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| Term.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.setCoe(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.mergeTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.isMergeable(Term) | 1.0 | 2.0 | 1.0 | 2.0 |
| Term.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getCoe() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.genFacLib(String[]) | 11.0 | 1.0 | 4.0 | 5.0 |
| Term.derive() | 5.0 | 1.0 | 3.0 | 3.0 |
| Term.dealMultiple(String) | 8.0 | 3.0 | 4.0 | 6.0 |
| MainClass.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.setCoe(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.mulFac(Fac) | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.getCoe() | 0.0 | 1.0 | 1.0 | 1.0 |
| Fac.Fac(BigInteger,BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.transExp(String) | 11.0 | 1.0 | 10.0 | 10.0 |
| Expression.toString() | 7.0 | 5.0 | 5.0 | 6.0 |
| Expression.sort(String) | 7.0 | 4.0 | 2.0 | 8.0 |
| Expression.mergeTerm() | 8.0 | 4.0 | 5.0 | 5.0 |
| Expression.getAnsString() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.genTermLib(String) | 5.0 | 1.0 | 4.0 | 4.0 |
| Expression.Expression(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 78.0 | 48.0 | 60.0 | 80.0 |
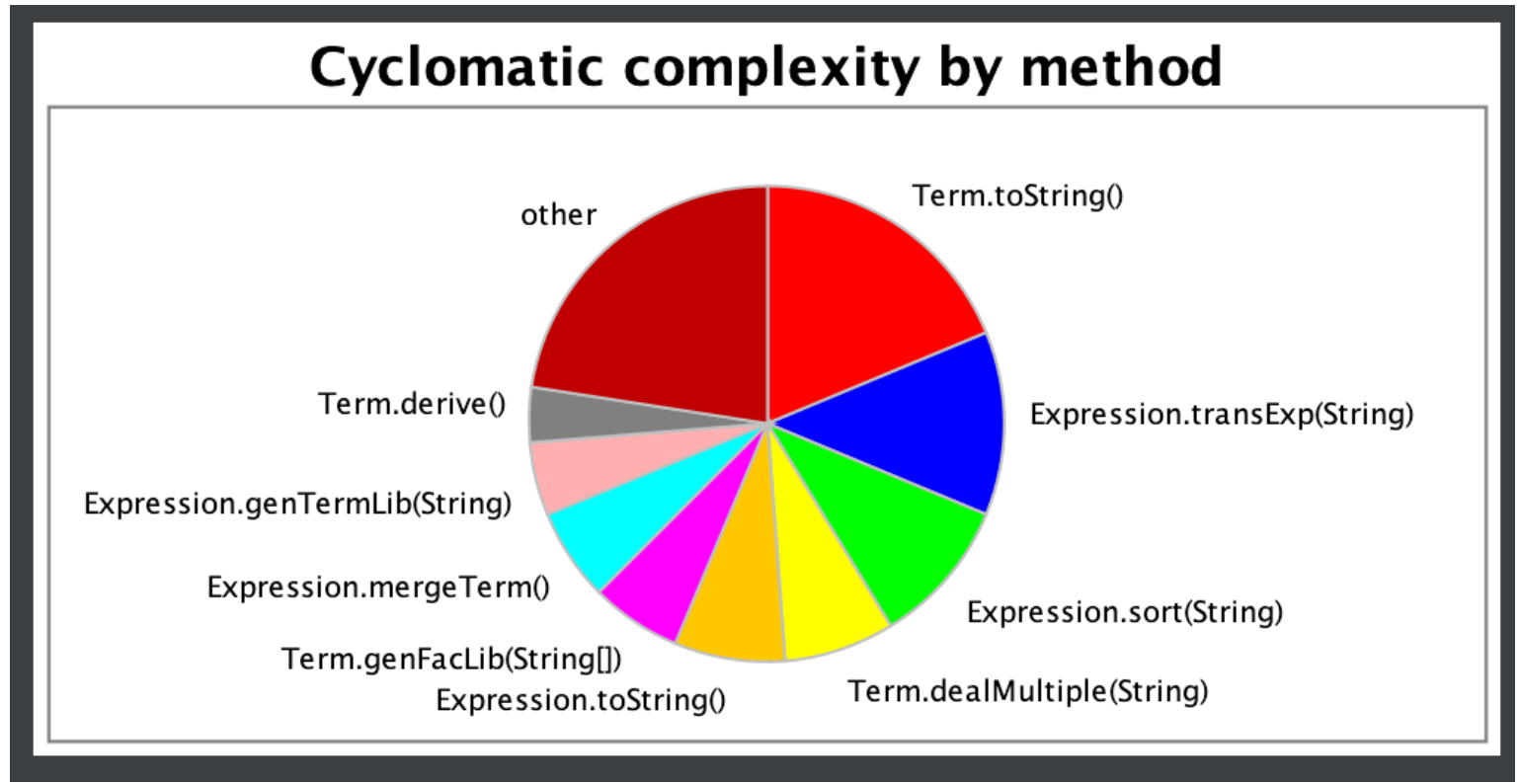
从上表可见,Term类中的toString方法圈复杂度较其他方法很高,主要原因是在判断和优化时过多次调用了toString。这个问题在第二次让我吃了大亏——为程序TLE埋下了可怕的种子。
第二次作业
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Sin.toString() | 2.0 | 3.0 | 1.0 | 3.0 |
| Sin.Sin(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.mulFac(Sin) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.getEs() | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.derive() | 1.0 | 2.0 | 1.0 | 2.0 |
| Sin.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| ProKilling.mergeToOne(Expression) | 18.0 | 1.0 | 13.0 | 13.0 |
| ProKilling.isConable(Item,Item) | 1.0 | 2.0 | 1.0 | 2.0 |
| Power.toString() | 2.0 | 3.0 | 1.0 | 3.0 |
| Power.Power(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.mulFac(Power) | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.getEp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.derive() | 1.0 | 2.0 | 1.0 | 2.0 |
| Power.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.toString() | 1.0 | 2.0 | 1.0 | 2.0 |
| Poly.toItem() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.Poly(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.Poly(Expression) | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.isItemable() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.derive() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| MultipleDerive.polyToItem(Expression) | 6.0 | 1.0 | 4.0 | 4.0 |
| MultipleDerive.mulDerive(Item) | 5.0 | 1.0 | 6.0 | 6.0 |
| MainClass.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.toString() | 3.0 | 3.0 | 5.0 | 6.0 |
| Item.setPolyList(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.setEs(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.setEp(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.setEc(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.setCoe(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.multi(Item) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.mulFac() | 6.0 | 1.0 | 5.0 | 5.0 |
| Item.merge(Item) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.linkPart() | 14.0 | 1.0 | 12.0 | 12.0 |
| Item.Item(String) | 1.0 | 1.0 | 1.0 | 2.0 |
| Item.Item(Const,Const,Const,Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.isMergeable(Item) | 1.0 | 2.0 | 1.0 | 2.0 |
| Item.isInteger(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getPolyList() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getEs() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getEp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getEc() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getCoe() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.genFactorList(String) | 9.0 | 1.0 | 5.0 | 5.0 |
| Item.definePart() | 12.0 | 1.0 | 5.0 | 9.0 |
| Item.dealMultiple(String) | 8.0 | 3.0 | 4.0 | 6.0 |
| Item.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.analyzeSign(String) | 8.0 | 1.0 | 6.0 | 8.0 |
| FactorFactory.createFactor(String) | 9.0 | 7.0 | 4.0 | 7.0 |
| Factor.getEs() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getEp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getEc() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.Factor() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.toString() | 13.0 | 8.0 | 8.0 | 10.0 |
| Expression.toItem() | 1.0 | 2.0 | 2.0 | 2.0 |
| Expression.splitPara(String) | 4.0 | 3.0 | 5.0 | 5.0 |
| Expression.merge() | 8.0 | 4.0 | 5.0 | 5.0 |
| Expression.isItemable() | 1.0 | 2.0 | 1.0 | 2.0 |
| Expression.getItemList() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.genTermList(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| Expression.Expression(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.Expression(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.derive() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.checkPara(String) | 6.0 | 3.0 | 3.0 | 5.0 |
| Expression.analyzeSign(String) | 19.0 | 1.0 | 8.0 | 19.0 |
| CreateFactorException.CreateFactorException() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.toString() | 2.0 | 3.0 | 1.0 | 3.0 |
| Cos.mulFac(Cos) | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.getEc() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.derive() | 1.0 | 2.0 | 1.0 | 2.0 |
| Cos.Cos(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.subtract(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.negate() | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.mul(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.Const(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.add(Const) | 0.0 | 1.0 | 1.0 | 1.0 |
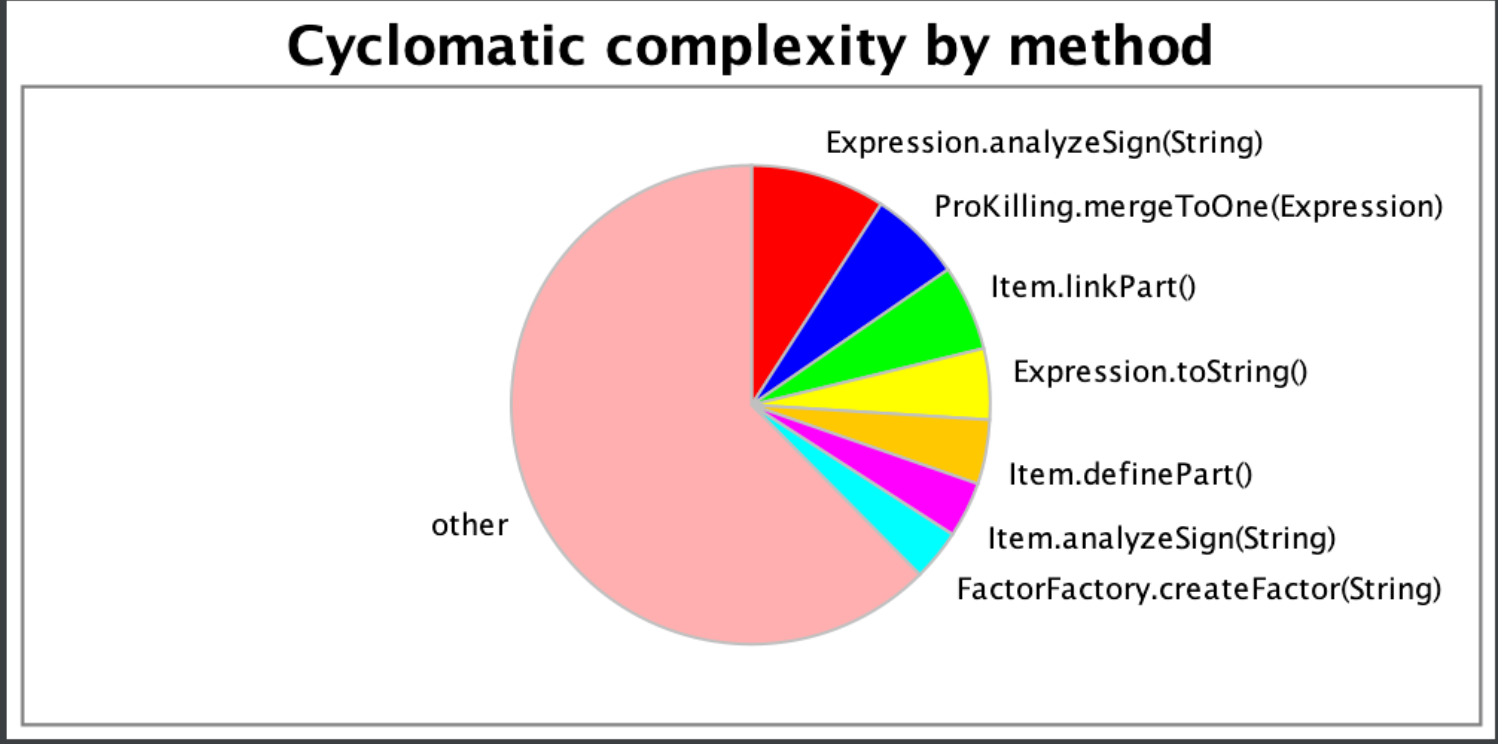
ProKilling.mergeToOne(Expression)是一个优化方法,把多个相同的项合并成一个;Item.linkPart()也是个优化方法,把多个因子合并成一个;Expression.analyzeSign(String)则是分析表达式的正负号,其调用了过多的toString等方法...
以上三个方法的复杂性较高,主要由于优化时没能做到针对部分优化,而是糅杂到了一起,也因此产生了很多bug。
第三次作业
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Const.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.Const(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Const.getCoe() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.Cos(BigInteger,Poly) | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.derive() | 3.0 | 3.0 | 3.0 | 4.0 |
| Cos.getPoly() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Cos.toString() | 2.0 | 3.0 | 3.0 | 3.0 |
| Expression.addItemList() | 7.0 | 5.0 | 2.0 | 5.0 |
| Expression.clone() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.derive() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.Expression(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.Expression(int) | 1.0 | 2.0 | 2.0 | 2.0 |
| Expression.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.getItems() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.isDigit() | 3.0 | 3.0 | 2.0 | 3.0 |
| Expression.keepReadSpace() | 3.0 | 3.0 | 2.0 | 3.0 |
| Expression.toString() | 8.0 | 5.0 | 4.0 | 6.0 |
| Factor.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.derive() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.Factor(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| FactorMaker.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| FactorMaker.keepReadSpace() | 3.0 | 3.0 | 2.0 | 3.0 |
| FactorMaker.makeConst() | 1.0 | 2.0 | 1.0 | 2.0 |
| FactorMaker.makeCos() | 7.0 | 7.0 | 2.0 | 7.0 |
| FactorMaker.makeFac(int) | 5.0 | 6.0 | 6.0 | 6.0 |
| FactorMaker.makePoly() | 1.0 | 2.0 | 1.0 | 2.0 |
| FactorMaker.makePow() | 4.0 | 4.0 | 2.0 | 4.0 |
| FactorMaker.makeSin() | 7.0 | 7.0 | 2.0 | 7.0 |
| Item.addFacList() | 9.0 | 4.0 | 3.0 | 5.0 |
| Item.analyzeSign() | 6.0 | 3.0 | 3.0 | 6.0 |
| Item.clone() | 1.0 | 1.0 | 2.0 | 2.0 |
| Item.derive() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getBase() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.isDigit() | 3.0 | 3.0 | 1.0 | 3.0 |
| Item.Item(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.Item(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.keepReadSpace() | 3.0 | 3.0 | 2.0 | 3.0 |
| Item.setBase(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.toString() | 5.0 | 5.0 | 3.0 | 6.0 |
| MainClass.main(String[]) | 3.0 | 3.0 | 2.0 | 4.0 |
| MulDerive.mulDerive(ArrayList,BigInteger) | 7.0 | 4.0 | 3.0 | 4.0 |
| Poly.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.derive() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.equals(Poly) | 1.0 | 2.0 | 1.0 | 2.0 |
| Poly.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.isContainOne() | 6.0 | 3.0 | 5.0 | 6.0 |
| Poly.isDigit() | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.Poly(Expression) | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.Poly(int) | 0.0 | 1.0 | 1.0 | 1.0 |
| Poly.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.derive() | 2.0 | 3.0 | 1.0 | 3.0 |
| Power.Power(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Power.toString() | 2.0 | 3.0 | 2.0 | 3.0 |
| RawString.getRaw() | 0.0 | 1.0 | 1.0 | 1.0 |
| RawString.RawString(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.clone() | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.derive() | 3.0 | 3.0 | 2.0 | 4.0 |
| Sin.getPoly() | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.Sin(BigInteger,Poly) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sin.toString() | 2.0 | 3.0 | 3.0 | 3.0 |
| ToSimplify.facIsMergeable(Factor,Factor) | 9.0 | 8.0 | 4.0 | 8.0 |
| ToSimplify.itemIsMergeable(Item,Item) | 10.0 | 7.0 | 5.0 | 8.0 |
| ToSimplify.simplifyExp(ArrayList) | 8.0 | 4.0 | 5.0 | 5.0 |
| ToSimplify.simplifyItem(ArrayList,BigInteger) | 8.0 | 4.0 | 5.0 | 5.0 |
| WrongFormatException() | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 145 | 163 | 130.0 | 181 |
| Average | 1.96 | 2.20 | 1.76 | 2.45 |

从上表可分析得出,ToSimplify化简相关方法的基本复杂度都相当高,这也是我经常因为化简出bug,且较难修复的主要原因;不仅如此,FactorMaker因子构造类中的每个方法基本复杂度都较高,这与优化过程中不断重新构造、递归构造因子有关;Item类的toString方法的基本复杂度也很高,这是因为在其他类,如上级Expression,化简ToSimplify,乘法MulDerive等类中都有调用toString方法,使得程序非结构化程度高。
除了以上三点,其他部分的耦合情况与复杂度都在一个较低水平上。
对类的度量分析
为了降低博客冗长性,这里只给出针对第三次作业的具体分析,一、二次作业将用Pie Chart饼图来更直观、清晰的展示。
第一次作业
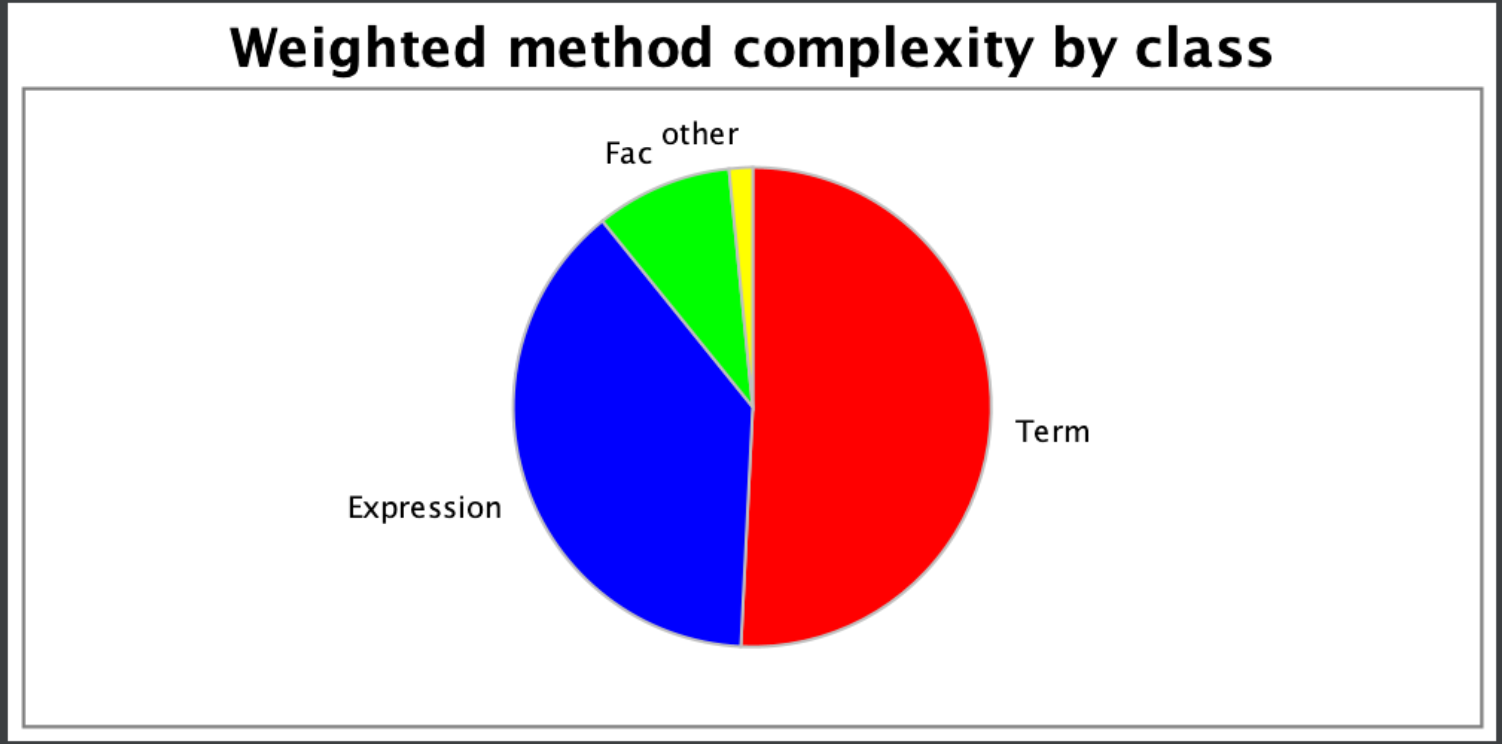
可见,第一次作业中Term承担的功能过多,未能实现较好的面向对象思想。
第二次作业
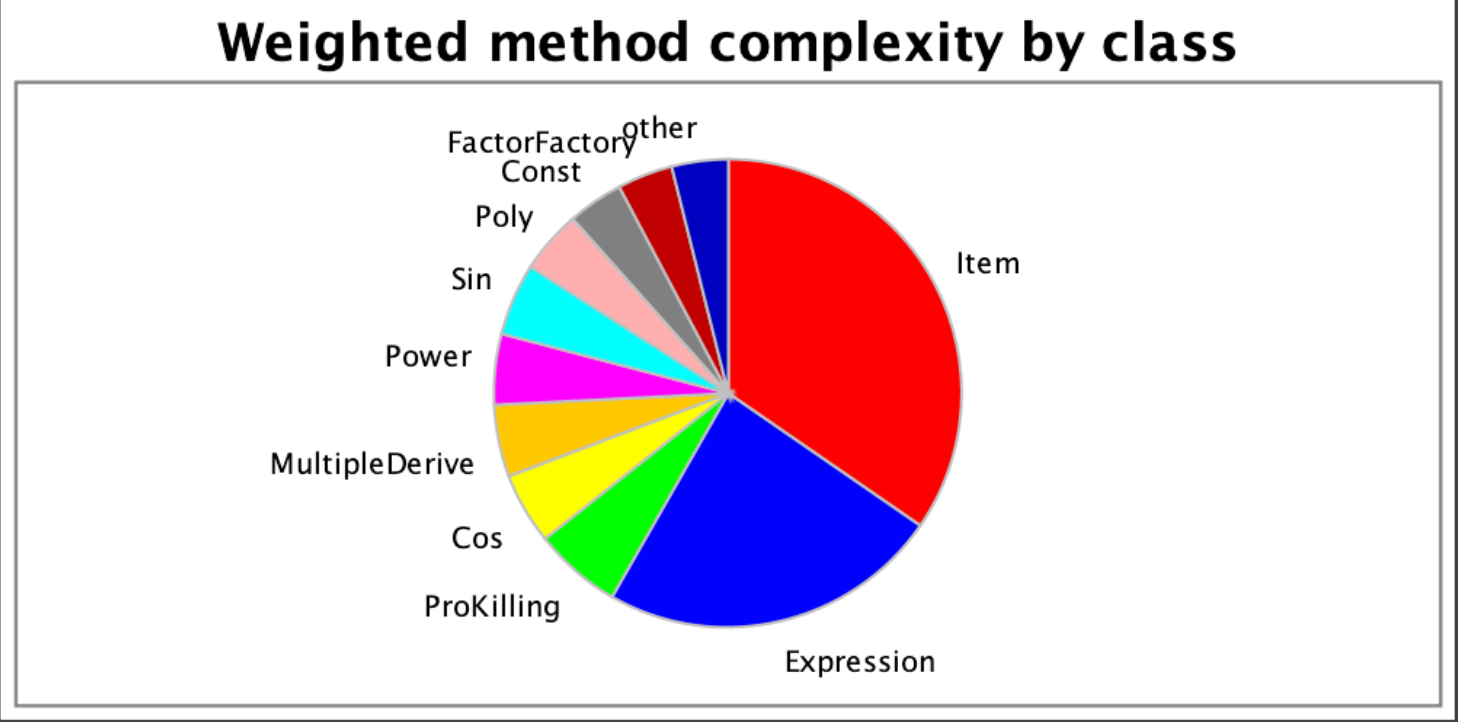
相比于第一次,这一次Item类承受的功能减少了,分配到了MultipleDerive/FactorFactory/ProKilling中了一些,降低了耦合性。
第三次作业
下表展示了第三次作业对每个类的度量分析,下面为名词解释。
OCavg:Average Operation Complexity,计算了非继承类中所有非抽象方法的平均圈复杂度。
OCmax:Maximum Operation Complexity,计算了非继承类中所有非抽象方法的最大圈复杂度。
WMC:Weighted Method Complexity,计算了每个类中的圈复杂度总和。
| Class | 属性个数 | OCavg | OCmax | WMC |
|---|---|---|---|---|
| Const | 1 | 1.0 | 1.0 | 3.0 |
| Cos | 2 | 1.83 | 4.0 | 11.0 |
| Expression | 3 | 2.6 | 6.0 | 26.0 |
| Factor | 1 | 1.0 | 1.0 | 5.0 |
| FactorMaker | 3 | 4.0 | 7.0 | 32.0 |
| Item | 3 | 2.38 | 6.0 | 31.0 |
| MainClass | 0 | 3.0 | 3.0 | 3.0 |
| MulDerive | 0 | 4.0 | 4.0 | 4.0 |
| Poly | 1 | 1.44 | 4.0 | 13.0 |
| Power | 1 | 1.8 | 3.0 | 9.0 |
| RawString | 1 | 1.0 | 1.0 | 2.0 |
| Sin | 2 | 1.83 | 4.0 | 11.0 |
| ToSimplify | 0 | 6.25 | 8.0 | 25.0 |
| WrongFormatException | 0 | 1.0 | 1.0 | 1.0 |

从上表与圈复杂度占权图中可以分析到,MulDerive求导类、ToSimplify化简类和FactorMaker因子构造类的复杂度较高,这与刚刚对各个类分析的结果一致。
从饼图可以对比看出,第三次作业每个类的职能更加平均分配了,没有出现像第一次某个类占一半多复杂度的情况,可见面向对象思想在三次作业中体现得愈加明显,类与类之间的耦合性也在逐步降低。
二、bug分析
第一次作业
暂时没有找到bug
第二次作业
1、TLE,程序在运行某些测试样例时会运行过慢,例如
(x*(x*(x*(x*(x*(x*(x*(x*(x*(x+1)+1)+1)+1)+1)+1)+1)+1)+1)+1)
- 原因:在优化过程中多次调用toString方法,在每个节点上造成了多倍的开销,整体性能变为指数级别。
- 解决方案:只需要把同一个函数里用到的相同的toString先存起来到一个变量里再调用就可以了,而不要每次使用都去做toString操作。
2、在解析类似于x*(-x+(-x))的项时会出现符号判断错误。
- 原因:在每个项与表达式前都进行了符号判断与解析,使得两次解析后反而错误。
- 解决方案:删除掉项前符号处理即可。
3、在对以下三角函数优化处理时,会出现莫名其妙的bug
- 原因:在进行判断时,只考虑了是否满足平方项,而忘记判断中间的符号是否为正。
- 解决方案:要么放弃此类三角函数优化,要么增加对符号的特殊判断。
第三次作业
1、忘记在sin、cos函数左括号后读空格,使得形如
的输入会被判定成Wrong Format!
- 原因:因为判断sin中是否为因子的操作是最后才想起来加的,因此在特判时考虑不周
- 解决方案:由于我写了keepReadSpace方法,因此在修复时主需要在判断因子前调用一下这个方法即可。
2、优化失误之,在对项合并时会误将指数上限设定为2
- 解决方案:关闭优化开关
| method | CogC | Ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| ToSimplify.simplifyItem(ArrayList,BigInteger) | 8.0 | 4.0 | 5.0 | 5.0 |
| ToSimplify.simplifyExp(ArrayList) | 8.0 | 4.0 | 5.0 | 5.0 |
| ToSimplify.itemIsMergeable(Item,Item) | 10.0 | 7.0 | 5.0 | 8.0 |
| ToSimplify.facIsMergeable(Factor,Factor) | 9.0 | 8.0 | 4.0 | 8.0 |
可见,除了第一个考虑不周的bug,主要的优化方法的圈复杂度出奇地高(其他在1.0、2.0左右)。
总结
三次作业的bug产生原因集中在优化失误上,无论是优化导致的toString调用过多,还是忘记某些条件,或是出现巨大漏洞,都启发我优化时一定要小心谨慎,多多进行测试。
且产生bug的地方往往圈复杂度很高,即耦合性高、非结构化程度高、可读性低。这提示着我以后在写程序时应该尽量降低类与类之间的复杂关联度,并且在完成时看一下各个方法的圈复杂度,以帮助我察觉隐蔽的bug。
三、测试策略
根据每次作业不同的复杂性,我采用了不同的测试方法
-
全自动测试程序->第一次作业。
由于第一次作业表达式较为简单,运算复杂度较低,因此我采用了全自动测试方法。
在Python中根据表达式可能的正则构造出长度不同、侧重点不同的测试数据,并链接外部java文件读入结果,进行格式处理,与Python自己计算结果进行比对。因为对两个结果做过一样的格式处理,因此每一个表达式只有唯一的标准答案。最后利用python的diff库来比对,如果不匹配,可以以可视化的形式显示出差异位置。
-
半自动测试程序->第二次与第三次作业。
在二、三次作业中,由于表达式逐渐复杂,考虑到自动生成的覆盖面窄、形式统一等问题,我采用了半自动测试方法。即不生成测试样例,但是对我输入的样例进行验证。
在朋友的指导与推荐下,我学会了将java文件打包成jar格式的方法,这样可以达到同时对7个同学进行测试的效果。且为了减轻评测机负担,验证正确性的方法从之前的形式比对验证,转换成了输入多个x值,验证标答与同学答案计算出结果的差异,失误率较低,且快捷。
-
构造测试样例->从一般到特殊
在每次作业完成后,我首先会人为构造一些测试样例来进行验证,此时要保证样例的全面性和特殊性,也要覆盖一些所谓的阴间数据。
例如,第一次作业的测试数据,涵盖了基础测试、大数、前导0、各种优化验证等方面。
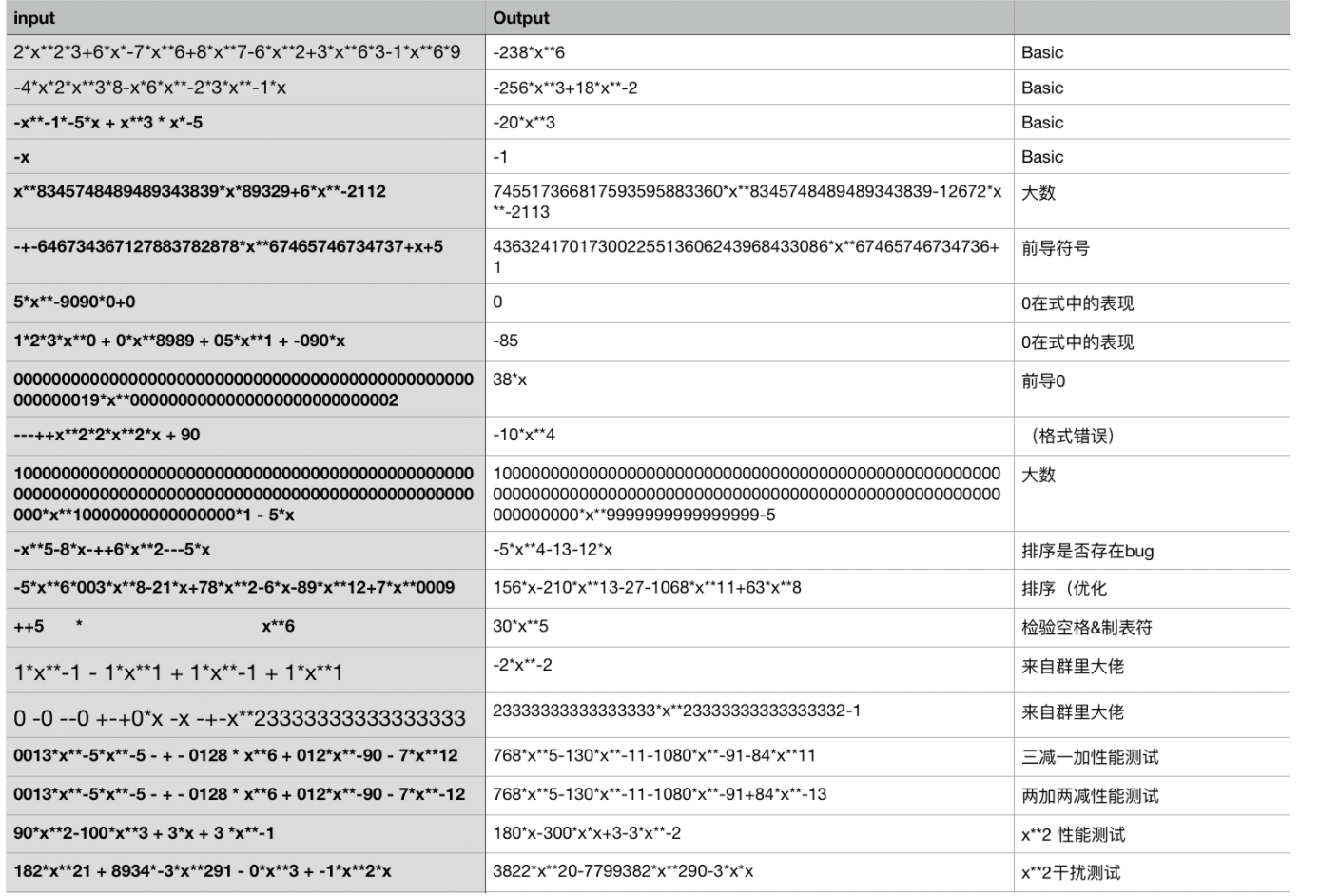
-
Hack策略
- 肉眼观察法。尤其注意其toString方法和解析字符串方法的设计,这两个很容易肉眼发现bug。
- 阴间数据测试法。对于一些自己踩过的坑,可以把坑放到其他人面前看会不会也掉下去。如第二次作业我的TLE数据也同样hack到了同组同学。
- 评测机无脑评测法。
四、重构经历
由于面向对象思想的不成熟、代码设计的不规范、逐步学习到高效的设计思路、对作业的理解逐步加深等原因,本人每次作业都在重构...
第一次->第二次
解析方法
第一次作业用了非常投机取巧的解析方法:把所有**替换成@,所有符合标准的+-替换成A+/A-,从而用split来分割,全程没用正则匹配;而这种方法显然不能继续用在第二次,于是第二次采用了括号拆分法,跳跃较大。
类图
第一次我只使用了四个类,没有继承与多态;而第二次作业则对因子、项与表达式分别存储,且引入了父类Factor,用继承实现,整体存储结构也从线性过渡到表达式树。
度量分析
第一次作业类的圈平均复杂度在2.60,而第二次则在2.25。可见虽然程序解决的问题更为复杂,但在对面向对象深入理解、重构后,圈复杂度反而降低了。
第二次->第三次
解析方法
在朋友和老师的安利下,第三次我终于采用了递归下降的方法解析表达式。不仅时间复杂度只有O(n),而且非常非常清晰易懂,几乎没有在解析中出现bug。
类图
二到三的类图变化不大,表达式树的关系也基本一致。
度量分析
第二次的圈平均复杂度在2.25,第三次在2.38。分析变高的原因,主要是由于写崩了的ToSimplify化简类复杂度实在太高,如果不算这个类,第三次的圈复杂度在2.17,相比第二次还是下降了的。
五、心得体会
-
不要有投机取巧的想法
由于第一次的投机取巧,第二次作业对我来讲完成难度过大,不仅完全重构,而且还要补上之前没学的知识,实在是害人害己。
-
慎重优化
纵观我的历次bug,几乎出在优化上,且第三次作业的圈复杂度还因为优化类被大大拖累。因此在优化前应该对整个程序有一个大的认识与思考,并一定要思考周全,不能妄为。
-
要利用好讨论区与同学的智慧
三次作业中,第二次作业被强测测出了bug。而此bug在我提交之前就已经发现了,但是一直无法解决。bug修复阶段向讨论区求助,得到了非常非常多同学们的回复与帮助。最后发现修复非常简单,只需要改不到4行代码。
可见如果早点在讨论区提问,也许可以规避此bug,也能帮到遇到同样问题的同学,悔不当初啊//
-
向前看,不要后悔
由于本人做了很多优化,又出了很多优化bug,因此可能要比其他放弃优化的同学用更多的时间写代码。但是在出bug-解决bug的过程中,我还是学到了挺多东西的。因此虽然很多优化看似白白浪费了时间还没用上,但——不能后悔


