上一节讲线性SVM时,文末提到在线性可分的情况下,找到一个支持向量,可求得b
但是当出现下图实例时,一些异常点导致的线性不可分
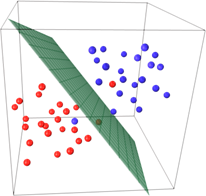
针对这种情况SVM提出了软间隔(soft margin),相对于硬间隔来说,简单将线性SVM看做硬间隔。
回顾硬间隔时优化目标:
min $\frac{1}{2}\left \| w_{2} \right \|_{2}^{2}$
$s.t y_{i}(w\cdot x_{i}+b)≥1$
在软间隔中,我们给每个样本点的函数距离减去了一个松弛变量( slack variable):
$y_{i}(w\cdot x_{i}+b)≥1-\xi $
且$\xi≥0$
Tips:
如何理解软间隔的几何含义?
原本我们希望有所的点到超平面的几何距离≥1,最后简化为函数距离。(这里不懂回顾线性SVM)
那么在超平面一侧的样本到超平面的函数距离最小为1,当减去$\xi$时,表明允许部分样本跨越支持向量,向着另一侧出发。
$\xi$还可以理解为离群点在另一侧时,该点到支持向量的函数距离。这样就引入了线性不可分问题。
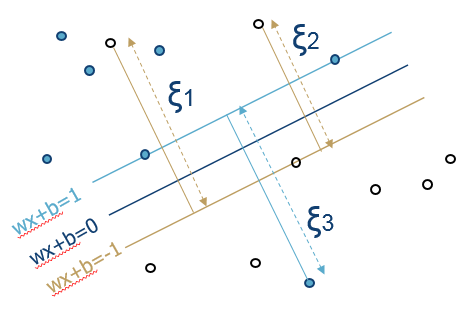
文末有详细的讨论过程。
但是这个松弛变量的加入是有代价的,我们在优化目标中加入了惩罚项(这里惩罚项可以看做是正则化)
min $\frac{1}{2}\left \| w_{2} \right \|_{2}^{2}+C\sum \xi _{i}$
$s.t y_{i}(w\cdot x_{i}+b)≥1-\xi$
$\xi≥0$
这里C>0,C越大表示我们对误分类惩罚越大,C可以根据样本点中重要程度调整。
优化目标函数:
$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}\left \| w \right \|_{2}^{2}+C\sum \xi _{i}-\sum \alpha _{i}\left [ y_{i}(w\cdot x_{i}+b)-1+\xi _{i} \right ]-\sum\mu _{i} \xi _{i}$
其中$\mu _{i}>0, \alpha _{i}>0$.(此处为什么大于零不懂去看KKT条件)
优化目标变成:
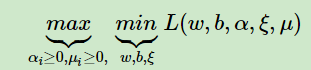
和线性SVM一样,对$w,b,\xi $求偏导
$\frac{\partial L}{\partial w}=0\Rightarrow w = \sum a_{i}y_{i}x_{i}$
$\frac{\partial L}{\partial b}=0\Rightarrow b = \sum a_{i}y_{i}$
$\frac{\partial L}{\partial \xi }=0\Rightarrow C-\alpha _{i}-\mu _{i}\Rightarrow C=\alpha _{i}+\mu _{i}$
带入L中,推导过程如下图(又是不知羞耻的盗图QAQ):

发现一件神奇的事情,这里最后的化解结果和线性SVM一模一样,当然总得有不一样的地方,就是约束条件
现在的优化目标如下:
$\underset{a}{max}=-\frac{1}{2}\sum \sum a_{i}a_{j}y_{i}y_{j}x_{i}\cdot x_{j}+\sum a_{i}$
$s.t \sum a_{i}y_{i}=0 (1)$
$C=\alpha _{i}+\mu _{i} (2)$
$\mu _{i}>0, \alpha _{i}>0 (3)$
由约束条件2和3可以得到$0\leqslant \alpha _{i}\leqslant C$
最后的优化目标成为:
$\underset{a}{min}=\frac{1}{2}\sum \sum a_{i}a_{j}y_{i}y_{j}\phi(x_{i}) \cdot\phi(x_{j})-\sum a_{i}$
$s.t \sum a_{i}y_{i}=0$
$0\leqslant \alpha _{i}\leqslant C$
与线性SVM相比仅仅多了一个约束条件$0\leqslant \alpha _{i}\leqslant C$,然后根据SMO算法得到$\alpha _{i}$,最后求w,b。
对松弛变量的简单理解:
在$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}\left \| w \right \|_{2}^{2}+C\sum \xi _{i}-\sum \alpha _{i}\left [ y_{i}(w\cdot x_{i}+b)-1+\xi _{i} \right ]-\sum\mu _{i} \xi _{i}$中,
根据软间隔最大化时KKT条件的对偶互补条件

(下图与文中Tips中的图不一样的地方是这里用的是离群点的几何距离)
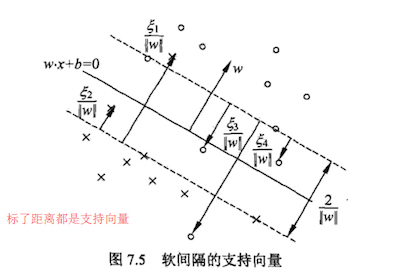
参考:


