接上一节KKT条件
感知机(perceptron)是理解神经网络和支持向量机的基础,值得我们认真学习。
感知机原理很朴素,功能也较为单一,即在样本线性可分的情况下,求得一个超平面P$\sum_{i=1}^{n}w _{i}\cdot x_{i}=0$,使得输入空间中的实例全部正确划分。
超平面的直观感受:

流程:
现有m个n维样本,n维简单理解为样本的特征(feature)个数。$x_{1}^{i},x_{2}^{i}···x_{n}^{i} ,y_{i}(i = 1,2,,,m,y=+1/-1)$
目标:找到超平面P$\sum_{i=1}^{n}w _{i}\cdot x_{i}=0$(令x0=1),使得输入空间实例,满足
一部分实例$\sum_{i=1}^{n}w _{i}\cdot x_{i}>0$,
另一部分实例$\sum_{i=1}^{n}w _{i}\cdot x_{i}<0$
令w=[θ0,···,θn],x=[x0,···,xn]
定义感知机模型$f(x)=sign(w\cdot x+b) ,( b=w _{0}\cdot x_{0} )$ , 其中

且,y=+1的实例有$w\cdot x+b>0$,
y=-1的实例有$w\cdot x+b<0$,这样定义是为了方便定义损失函数
定义损失函数为误分类点到超平面P的距离。我们希望的是误分类点到超平面P的距离最小
有点到平面的距离$d=\frac{\left | w\cdot x_{i}+b \right |}{\left \| w \right \|_{2}}$
Tips:
点到超平面的距离的理解
类似与解析几何
Ax+By+C=0,点(x0,y0)到平面的距离为
$d=\frac{Ax_{0}+By_{0}+C}{\sqrt{A^{2}+B^{2}}}$,
所以点到超平面P的距离为$d=\frac{\left | w\cdot x_{i}+b \right |}{\left \| w \right \|_{2}}$
其中,$\left \| w \right \|_{2}$为L2范数,简单理解L2范数就是欧几里得距离
就误分类的点必有-yi(w·xi+b)>0,等价于$\left | w\cdot x_{i}+b \right |>0$,所以
$d=\frac{-y\left | w\cdot x_{i}+b \right |}{\left \| w \right \|_{2}}$
设误分类点集合M,有
$d=-\frac{1}{\left \| w \right \|_{2}}\sum_{x_{i}\subseteq M}^{ }y_{i}(w\cdot x_{i}+b)$
我们发现,点到平面距离 d 的分子分母均有W,即分子分母成倍数关系,我们可以固定分子或分母为1,来简化损失函数。
在感知机模型中,常常保留分子,最终感知机损失函数L为:
$L\left ( w,b \right )=-\sum_{x_{i}\subseteq M}^{ }y_{i}(w\cdot x_{i}+b)$
感知机优化:
采用随机梯度下降法,通过误分类点来更新梯度
损失函数求偏导:
$\frac{\partial }{\partial w}L\left ( w,b \right )=-\sum_{x_{i}\subset M}^{ }y_{i}x_{i}$
$\frac{\partial }{\partial b}L\left ( w,b \right )=-\sum_{x_{i}\subset M}^{ }y_{i}$
$w=w-\eta (-\sum_{x_{i}\subset M}^{ }y_{i}x_{i})$
$w=w+\eta \sum_{x_{i}\subset M}^{ }y_{i}x_{i}$
其中,$\eta $为步长,yi=-1/+1,x为已知样本
对偶形式:
没有实践,纸上谈兵,不做太多赘述。
个人理解为,通过查询Gram矩阵来选择一个误分类点,一次內积运算节省了时间。
参考:https://www.bilibili.com/video/av23933161/?p=20
http://www.cnblogs.com/pinard/p/6042320.html
实例
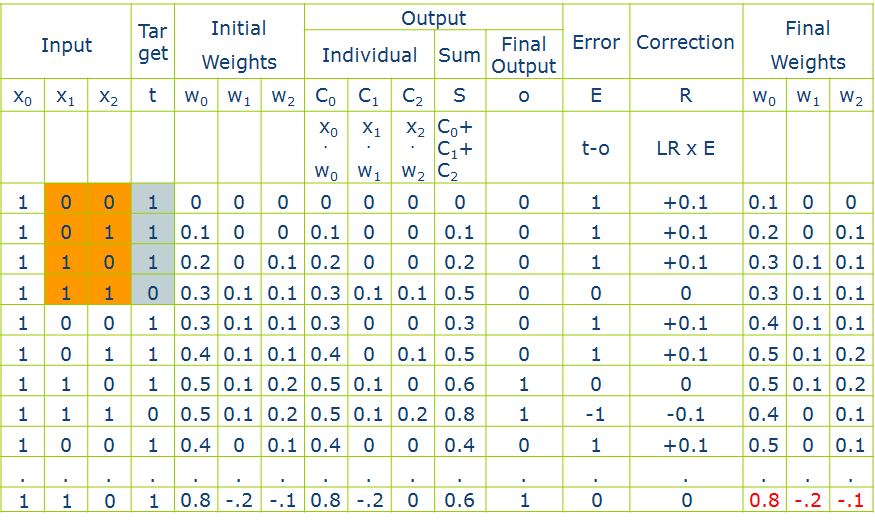
四个样本,两个维度,一个Y(如图标黄的部分),设定sign函数>0.5为1,≤0.5为0,学习速率即步长为0.1
我简单讲解一行
每个超平面(每一行)都设定x0都为1,将第一个样本带入(0,0,1)--input和target,对应的初始权重(initial weights),1×0+0×0+0×0=0(output,sum)因为sign该函数的规定,0<0.5,所以final output=0,误差error等于target-final output=t-o=1-0=1(得到正确的解时每一行都应为0,比如最后一行)
更新w,W0=W0+η×Y×X0=0+0.1×1×1=0.1,W1=W1+η×Y×X1=0+0.1×0×0=0,,,,,以此类推