Karush–Kuhn–Tucker conditions
接第一节,拉格朗日乘子法https://www.cnblogs.com/super-yb/p/10705789.html
我先直接给出公式(别跑!),然后慢慢解释每一条内容,欢迎批评指正!
我们优化的目标是:
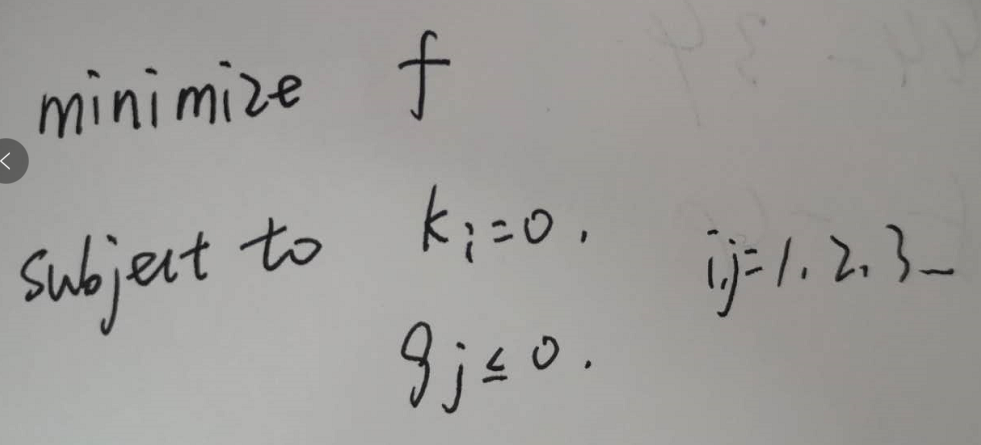
其中,KKT条件如下:
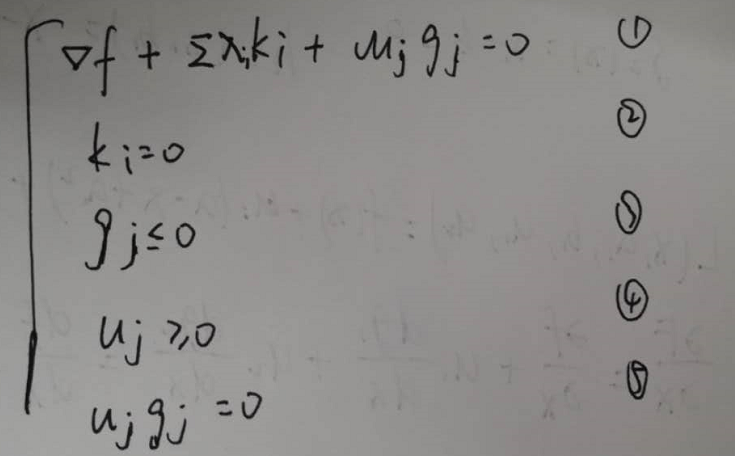
公式1、2、3不多解释。
公式4、5,通过一个简单例子说明:
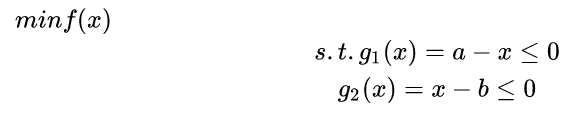
gi添加一个 ≥0 的松弛变量![]() 、
、![]() 。得到
。得到
由此,我们将不等式转化为等式约束,应用拉格朗日乘子法。
拉格朗日方程如下:
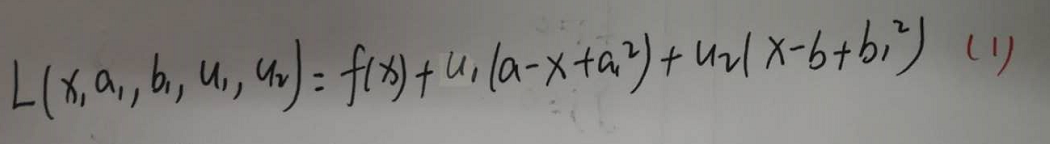
对方程求偏导如下:

注意红笔写的条件,我们会稍后解释。
那么现在开始解方程组
首先考虑 式5,
当u1=0,a1≠0时,即 g1 对f(x)无约束
当u1≠0,a1=0时,即 g1 对f(x)有约束,且根据式3可知, g1 也等于0。
式6同理。注意,不等式对f(x)有约束效果时,不等式等于零。
此时,方程组简化成
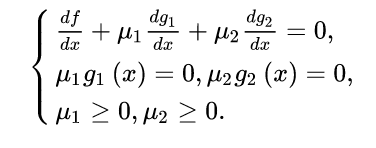
推广,对于多个不等式约束,有
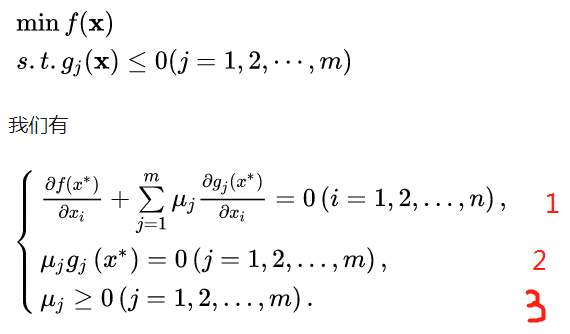
上述不等式称之为KKT条件,与本文一开始略有不同的是没有了等式的约束(不用在此纠结,我们关心的是不等式的约束问题),其中uj称之为KKT乘子
最后利用几何的角度说明,为什么在极值点处KKT乘子大于等于零?
其实用一个不等式约束很好理解,类似拉格朗日乘子法,
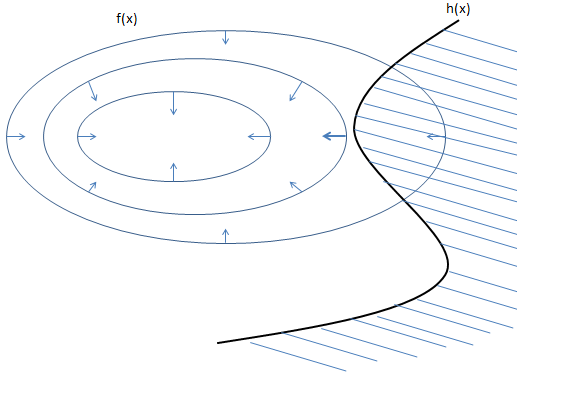
f(x)的负梯度与g(x)的梯度同向,所以u1≥0.
现增加一个不等式约束。
将式1用梯度表示并移项,
![]()
x*表示极值点。
那么,此时f(x)的负梯度可以表示成所有有效约束条件在该点梯度的线性组合,梯度为向量,且与等高线垂直,有效指的是该约束条件(不等式)对应的KKT乘子。
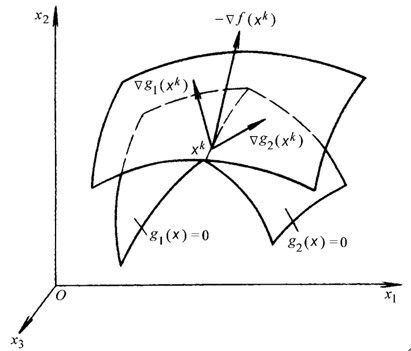
如图,极值点XK一定落在g1(X)=0和g2(X)=0两平面的交线上,且点XK处f(x)的负梯度可以为g1(X)和g2(X)梯度的线性组合。考虑两种情况:
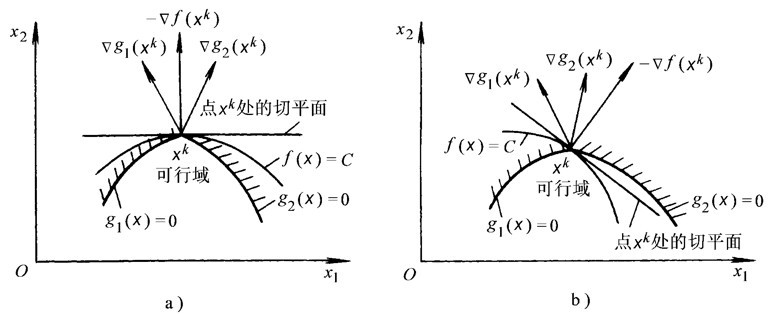
注意,由于约束条件为不等式,所以极值点的可行域为下半平面。
当在b情况时,(ui小于0)在可行域C值可以变化,所以这种情况极值点不是最优。如图
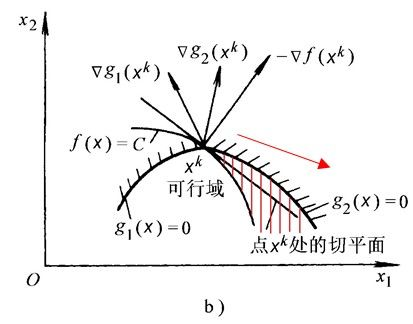
在a情况下,ui≥≥0,当C发生变化时,约束条件破坏,即该点为局部最优点。
接下一节感知机
参考:https://www.matongxue.com/madocs/987.html
https://zhuanlan.zhihu.com/p/26514613
https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions
https://www.cnblogs.com/liaohuiqiang/p/7805954.html
https://www.cnblogs.com/xinchen1111/p/8804858.html
最后附一个拉格朗日对偶问题讲的很好的博文


