网上博文与教学视频的结合+自我总结,难免有错,欢迎交流,多多指教!
拉格朗日乘子法(lagrange multipier)
即带有等式约束的优化问题,公式如下:
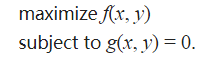
之后建立拉格朗日函数:
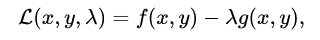
λ即为拉格朗日乘子。之后将该函数分别对x,y,λ求偏导即可。现在我们试图阐明该方法的原理。
举实例:min f(x,y) = x2 + y2,
s.t. g(x,y) = x2y , g = 3
下图为g(x,y)的等高线(contour),蓝色为 g = 3 时的投影。
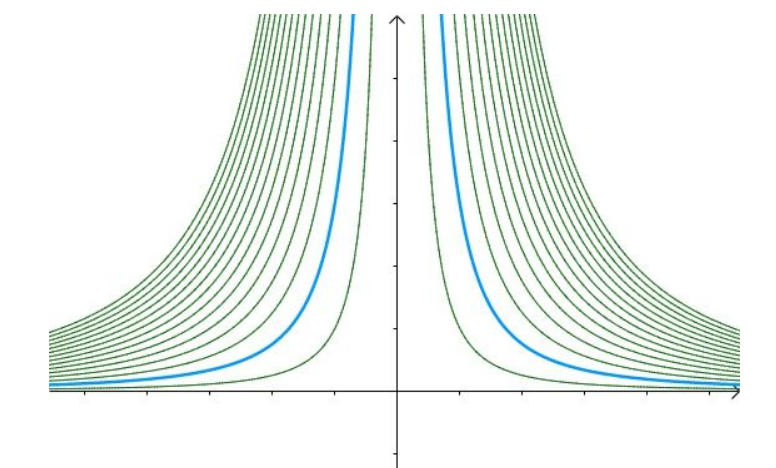
下图为f(x,y)的等高线,为直观,我放两张图
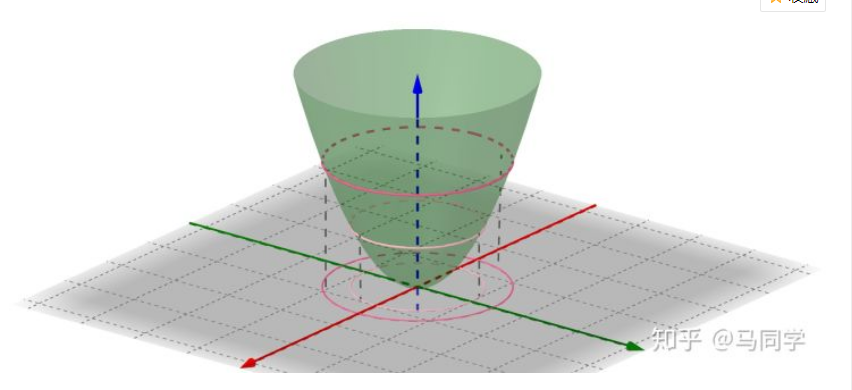

而我们要求的解 在这
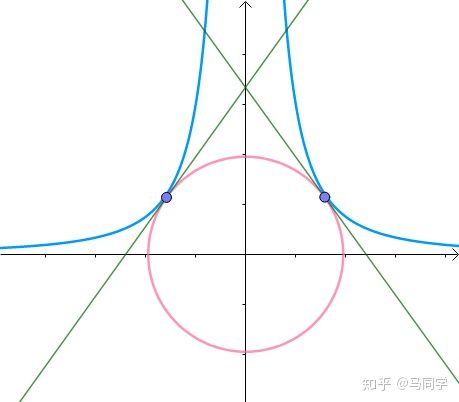
有什么特殊?1 两等高线相切;2 切线的法向量平行,而法向量就是函数的梯度(此处有不理解以后会更新)。
那么有 :

化简:

而我们的拉格朗日函数求解时为

看到这,我想应该,明白了wiki上的那副经典的图片了,上图
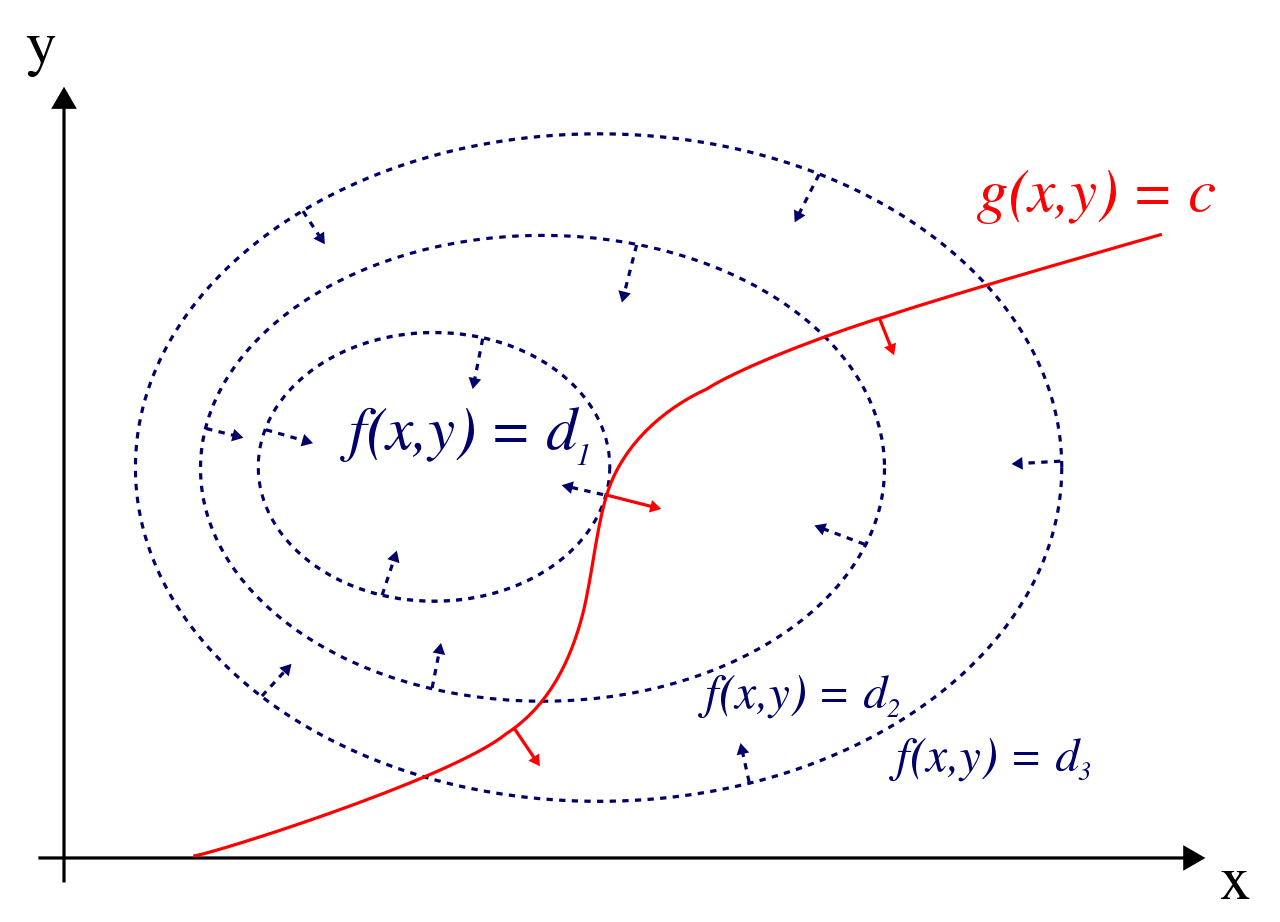
同时,博文3中的这句话也能理解了:
假设g(x)与等高线相交,交点就是同时满足等式约束条件和目标函数的可行域的值,但肯定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优值,如下图所示,即等高线和目标函数的曲线在该点的法向量必须有相同方向,所以最优值必须满足:f(x)的梯度 = a* g(x)的梯度
而支持向量机中常用到的KKT条件,请参见下文https://www.cnblogs.com/super-yb/p/10811713.html
参考:Lagrange multiplier - Wikipedia https://en.wikipedia.org/wiki/Lagrange_multiplier
https://www.zhihu.com/question/38586401/answer/105273125
https://blog.csdn.net/xianlingmao/article/details/7919597



