图像标注 python实现-普通RNN篇
RNN介绍
神经网络包含输入层、隐层、输出层,通过激活函数控制输出,层与层之间通过权值连接。激活函数是事先确定好的,那么神经网络模型通过训练“学“到的东西就蕴含在“权值“中。
RNN与普通神经网络最大的不同就是建立了时序和状态的概念,即某个时刻的输出依赖与前一个状态和当前的输入,所以RNN可以用于处理序列数据。
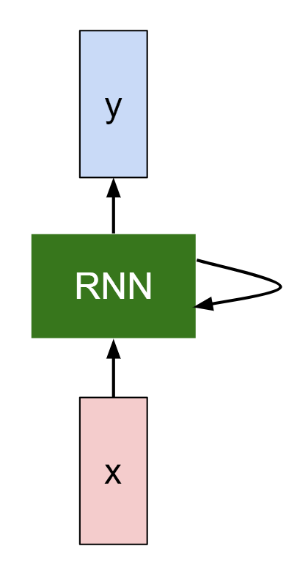 展开之后
展开之后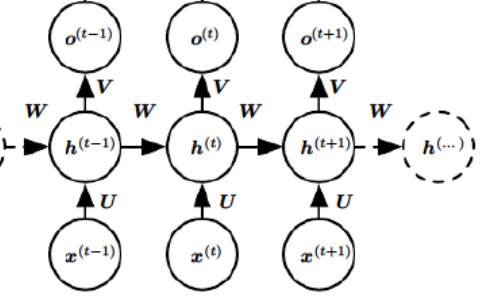
箭头上的字母代表权重矩阵,也就是不同层之间的连接。x代表输入序列,h代表状态,也就是时刻,o代表输出。
可以看到,整个网络是共享W、U、V三个矩阵的,这样的设计主要有两个好处:
(1)收敛快。参数越少越容易收敛
(2)可以想要有多少层就有多少层。因为权重就是固定的这三个,所以每次训练或者测试的数据长度不需要相等,比较灵活。
这是多输出对多输出的,RNN还有很多其他灵活的变体,可以根据不同的场景选择:
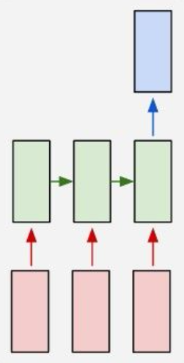
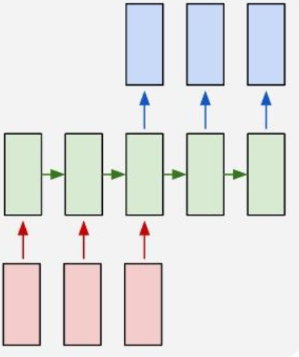
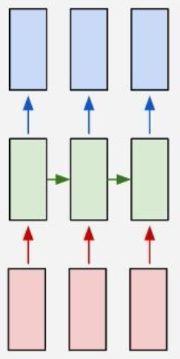
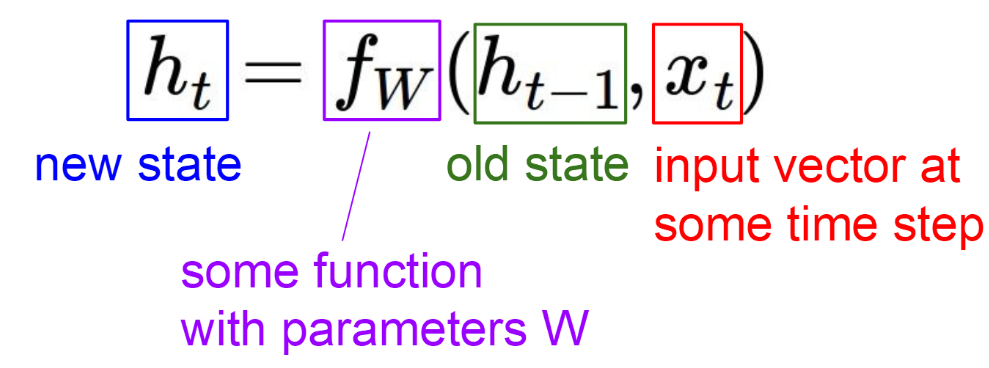
前向传播:
对于t时刻:
$$h^{(t)}=f_{w}(W*h^{(t-1)}+U*x^{t}+b)$$
其中是$f_{w}$激活函数,一般来说会选择tanh函数,原因见下面激活函数介绍,b为偏置。
t时刻的输出:
$$o^{(t)}=V*h^{(t)}+c$$
最终模型的预测输出为:
$$y^{(t)}=\sigma(o^{(t)})$$
通常最后的单时刻任务还是分类,所以激活函数$\sigma$选用softmax函数。
所有的y按时刻顺序组织起来就是最终输出。
反向传播:
RNN的反向传播跟普通的神经网络反向传播从本质上来说都是链式求导,没有什么太大的区别。
需要注意的就是权重就共享的,所以梯度需要累加,最后传播到$h_{0}$的时候更新一次就行。
求导并不难,只是堆在一起之后比较复杂,看起来比较吓人,用链式法则一步一步求就好了,这里就不写公式了,编辑比较麻烦。
想看具体怎么反向传播的公式可以直接看代码。
激活函数:
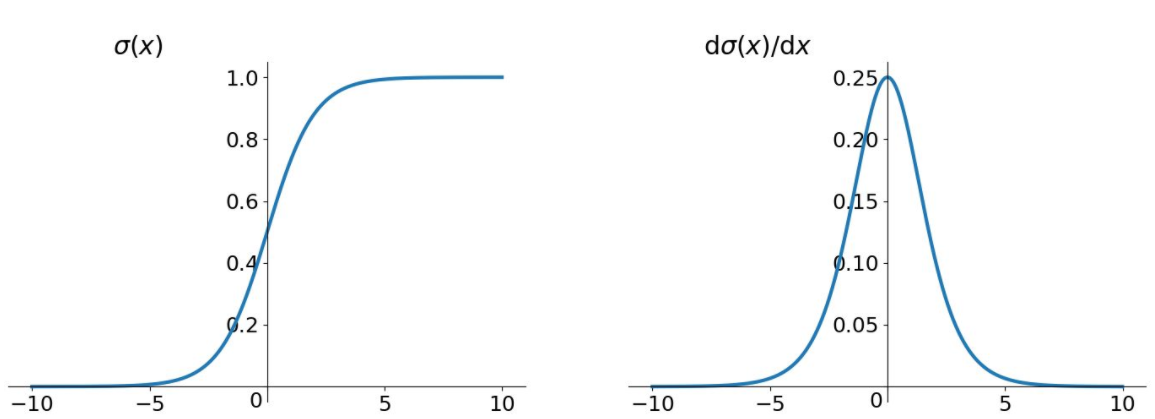
sigmoid函数图像和导数图像
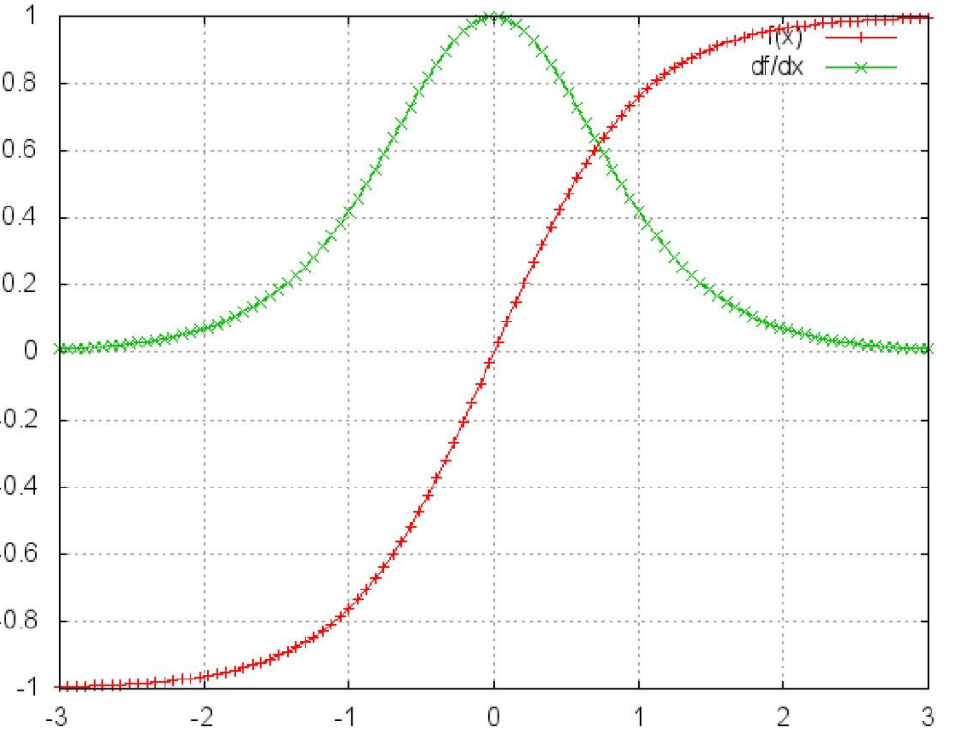
tanh函数的图像和导数图像
二者的函数图像很相似,都把输出压缩在了一个范围之内。他们的导数图像也非常相近,,sigmoid函数的导数范围是(0,0.25],tanh函数的导数范围是(0,1],他们的导数最大都不大于1。这就会导致一个问题,在上面式子累乘的过程中,是一堆小数相乘,会越乘越小,随着时间序列的不断深入,小数的累乘就会导致梯度越来越小直到接近于0,这就是“梯度消失“现象。在较为深层的神经网络中会导致反向传播时梯度消失,梯度消失就意味消失那一层的参数再也不更新,那么那一层隐层就变成了单纯的映射层,毫无意义。但是看起来tanh会比sigmoid消失的更加慢一些,所以这里选用tanh函数。
还有一个原因是sigmoid函数还有一个缺点,Sigmoid函数输出不是零中心对称。sigmoid的输出均大于0,这就使得输出不是0均值,称为偏移现象,这将导致后一层的神经元将上一层输出的非0均值的信号作为输入。关于原点对称的输入和中心对称的输出,网络会收敛地更好。
图像标注:
有了上面的基础,接下来就可以进入正题了。
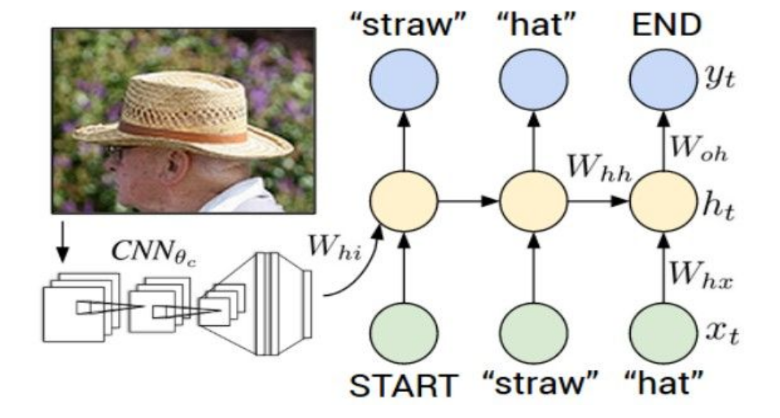
首先对输入的图像用CNN进行处理,得到降维的特征(这里直接用VGG16的fc7的输出),然后把正确标注和特征送入RNN。
在实际应用中,对单词直接处理比较不方便,所以一般会把单词映射成一个整数,这样就变成了一个分类问题。编码过程由word_embedding_forward函数完成。
好了详细的内容直接上代码吧。
RNN.py就一个类,定义网络结构
1 import numpy as np 2 3 from cs231n.layers import * 4 from cs231n.rnn_layers import * 5 6 class CaptioningRNN(object): 7 """ 8 这个类只是构建RNN的网络结构和定义内部计算 9 具体的权值更新训练过程不在这里实现 10 """ 11 12 def __init__(self, word_to_idx,input_dim=512,wordvec_dim=128, 13 hidden_dim=128,cell_type='rnn',dtype=np.float32): 14 15 ''' 16 - word_to_idx: 字典,存储了单词到整数的映射关系. 17 - input_dim: 单个输入的维度 18 - wordvec_dim: 单词向量的维度. 19 - hidden_dim: 隐层的大小. 20 - cell_type: 'rnn' or 'lstm'. 21 ''' 22 if cell_type not in {'rnn','lstm'}: 23 raise ValueError('Invalid cell type "%s"' %cell_type) 24 25 self.cell_type=cell_type 26 self.dtype=dtype 27 self.word_to_idx=word_to_idx 28 self.idx_to_word={i:w for w,i in word_to_idx.items()} 29 self.params={} 30 31 vocab_size=len(word_to_idx) 32 self._null=word_to_idx['<NULL>'] 33 self._start=word_to_idx.get('<START>',None) 34 self._end=word_to_idx.get('<END>',None) 35 36 #初始化代表每个单词的向量 37 self.params['W_embed']=np.random.randn(vocab_size,wordvec_dim) 38 self.params['W_embed']/=100 39 40 #由CNN的输出向RNN的第一层转换 41 #注意:给的输入数据已经是经过VGG16提取的特征,所以这里没有CNN层 42 self.params['W_proj']=np.random.randn(input_dim,hidden_dim) 43 self.params['W_proj']/=np.sqrt(input_dim) 44 self.params['b_proj']=np.zeros(hidden_dim) 45 46 #初始化RNN的参数,每一层共享参数,所以参数只需要设置一次 47 48 ####################这里的4是什么意思???????????见下回lstm分解 49 dim_mul={'lstm':4,'rnn':1}[cell_type] 50 self.params['Wx']=np.random.randn(wordvec_dim,dim_mul*hidden_dim) 51 self.params['Wx']/=np.sqrt(wordvec_dim) 52 self.params['Wh']=np.random.randn(hidden_dim,dim_mul*hidden_dim) 53 self.params['Wh']/=np.sqrt(hidden_dim) 54 self.params['b']=np.zeros(dim_mul*hidden_dim) 55 56 #得到每个时间点的输出,输出是每个单词的得分 57 self.params['W_vocab']=np.random.randn(hidden_dim,vocab_size) 58 self.params['W_vocab']/=np.sqrt(hidden_dim) 59 self.params['b_vocab']=np.zeros(vocab_size) 60 61 #强制转换,保证每个权重矩阵都是我们设置的数据类型 62 for k,v in self.params.items(): 63 self.params[k]=v.astype(self.dtype) 64 65 def loss(self,features,captions): 66 """ 67 Inputs: 68 - features: 输入的特征,shape (N, D) 69 - captions: Ground-truth; 数组,shape (N, T),N张图片都用T个单词描述 70 71 Returns a tuple of: 72 - loss: Scalar loss 73 - grads: Dictionary of gradients parallel to self.params 74 75 返回loss和梯度(如果是训练过程) 76 77 """ 78 79 #输入的描述和输出的描述对完整的描述有点区别 80 #具体在于输入去掉最后一个单词'<end>' 输出去掉第一个单词'<start>' 81 #因为输入第一个单词的时候就已经需要预测下一个单词了 所以有一个单词的错位 82 captions_in=captions[:,:-1] 83 captions_out=captions[:,1:] 84 85 #每个描述长度有所不同,短的用NULL补齐到T长度,所以NULL不计入loss 86 mask=(captions_out!=self._null) 87 88 W_proj,b_proj=self.params['W_proj'],self.params['b_proj'] 89 W_embed=self.params['W_embed'] 90 Wx,Wh,b=self.params['Wx'],self.params['Wh'],self.params['b'] 91 W_vocab,b_vocab=self.params['W_vocab'],self.params['b_vocab'] 92 93 #前向计算过程: 94 #(1)使用仿射函数将从CNN提取的特征转换到第一个RNN的隐层状态(N,H) 95 #(2)将captions_in从单词转换成向量(N,T,W) 96 #(3)在RNN各个隐层中进行运算,(N,T,H) 97 #(4)在每个时间点计算各个单词的得分(N,T,V) 98 #(5)用softmax计算各时间点的loss 99 # W表示单词向量的维度 V表示单词词库的个数 100 loss,grads=0.0,{} 101 102 #begin 103 104 affine_out,affine_cache=affine_forward(features,W_proj,b_proj) 105 106 word_embedding_out,word_embedding_cache=word_embedding_forward(captions_in,W_embed) 107 108 if self.cell_type=='rnn': 109 rnn_or_lstm_out,rnn_cache=rnn_forward(word_embedding_out,affine_out,Wx,Wh,b) 110 elif self.cell_type=='lstm': 111 rnn_or_lstm_out,lstm_cache=lstm_foward(word_embedding_out,affine_out,Wx,Wh,b) 112 else: 113 raise ValueError('Invalid cell type "%s"' %self.cell_type) 114 115 temporal_affine_out,temporal_affine_cache=temporal_affine_forward(rnn_or_lstm_out,W_vocab,b_vocab) 116 117 ''' 分割线''' 118 loss,dtemporal_affine_out=temporal_softmax_loss(temporal_affine_out,captions_out,mask) 119 120 #反向传播 121 drnn_or_lstm_out,grads['W_vocab'],grads['b_vocab']=temporal_affine_backward(dtemporal_affine_out,temporal_affine_cache) 122 123 if self.cell_type=='rnn': 124 dword_embedding_out,daffine_out,grads['Wx'],grads['Wh'],grads['b']=rnn_backward(drnn_or_lstm_out,rnn_cache) 125 else: 126 dword_embedding_out,daffine_out,grads['Wx'],grads['Wh'],grads['b']=lstm_backward(drnn_or_lstm_out, lstm_cache) 127 128 grads['W_embed']=word_embedding_backward(dword_embedding_out,word_embedding_cache) 129 130 dfeatures,grads['W_proj'],grads['b_proj']=affine_backward(daffine_out,affine_cache) 131 132 #end 133 134 return loss,grads 135 136 137 def sample(self,features,max_len=30): 138 ''' 139 预测 140 RNN与CNN不同,CNN的预测和训练过程没有区别 141 但是RNN不同,训练过程每个时刻都有输入,但是预测的时候根本没有输出怎么办? 142 还好我们有个<start>,可以当作第一个时刻的输入,可以得到第一个时刻的输出,把第一个时刻的输出当作第二个时刻的输入 143 依次类推 144 ''' 145 N,D=features.shape 146 captions=self._null*np.ones((N,max_len),dtype=np.int32) 147 148 W_proj, b_proj = self.params['W_proj'], self.params['b_proj'] 149 W_embed = self.params['W_embed'] 150 Wx, Wh, b = self.params['Wx'], self.params['Wh'], self.params['b'] 151 W_vocab, b_vocab = self.params['W_vocab'], self.params['b_vocab'] 152 153 affine_out,affine_cache=affine_forward(features,W_proj,b_proj) 154 prev_word_idx=[self._start]*N 155 prev_h=affine_out 156 prev_c=np.zeros(prev_h.shape) 157 captions[:,0]=self._start 158 159 for i in range(1,max_len): 160 prev_word_embed=W_embed[prev_word_idx] 161 if self.cell_type=='rnn': 162 next_h,rnn_step_cache=rnn_step_forward(prev_word_embed,prev_h,Wx,Wh,b) 163 elif self.cell_type=='lstm': 164 pass 165 else: 166 raise ValueError('Invalid cell_type "%s"' % self.cell_type) 167 vocab_affine_out,vocab_affine_cache=affine_forward(next_h,W_vocab,b_vocab) 168 captions[:,i]=list(np.argmax(vocab_affine_out,axis=1)) 169 prev_word_idx=captions[:,i] 170 prev_h=next_h 171 172 return captions
layer.py 分步实现各个层之间的计算 import numpy as np """ This file defines layer types that are commonly used for recurrent neural networks. """ def rnn_step_forward(x, prev_h, Wx, Wh, b): """ Run the forward pass for a single timestep of a vanilla RNN that uses a tanh activation function. Inputs: - x: Input data for this timestep, of shape (N, D). - prev_h: Hidden state from previous timestep, of shape (N, H) - Wx: Weight matrix for input-to-hidden connections, of shape (D, H) - Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H) - b: Biases of shape (H,) Returns a tuple of: - next_h: Next hidden state, of shape (N, H) - cache: Tuple of values needed for the backward pass. """ next_h, cache = None, None ############################################################################## # TODO: Implement a single forward step for the vanilla RNN. Store the next # # hidden state and any values you need for the backward pass in the next_h # # and cache variables respectively. # ############################################################################## a=prev_h.dot(Wh)+x.dot(Wx)+b next_h=np.tanh(a) cache=(x,prev_h,Wh,Wx,b,next_h) return next_h, cache def rnn_step_backward(dnext_h, cache): """ Backward pass for a single timestep of a vanilla RNN. Inputs: - dnext_h: Gradient of loss with respect to next hidden state - cache: Cache object from the forward pass Returns a tuple of: - dx: Gradients of input data, of shape (N, D) - dprev_h: Gradients of previous hidden state, of shape (N, H) - dWx: Gradients of input-to-hidden weights, of shape (D, H) - dWh: Gradients of hidden-to-hidden weights, of shape (H, H) - db: Gradients of bias vector, of shape (H,) """ dx, dprev_h, dWx, dWh, db = None, None, None, None, None ############################################################################## # TODO: Implement the backward pass for a single step of a vanilla RNN. # # # # HINT: For the tanh function, you can compute the local derivative in terms # # of the output value from tanh. # ############################################################################## x,prev_h,Wh,Wx,b,next_h=cache da=dnext_h*(1-next_h*next_h) dx=da.dot(Wx.T) dprev_h=da.dot(Wh.T) dWx=x.T.dot(da) dWh=prev_h.T.dot(da) db=np.sum(da,axis=0) return dx, dprev_h, dWx, dWh, db def rnn_forward(x, h0, Wx, Wh, b): """ Run a vanilla RNN forward on an entire sequence of data. We assume an input sequence composed of T vectors, each of dimension D. The RNN uses a hidden size of H, and we work over a minibatch containing N sequences. After running the RNN forward, we return the hidden states for all timesteps. Inputs: - x: Input data for the entire timeseries, of shape (N, T, D). - h0: Initial hidden state, of shape (N, H) - Wx: Weight matrix for input-to-hidden connections, of shape (D, H) - Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H) - b: Biases of shape (H,) Returns a tuple of: - h: Hidden states for the entire timeseries, of shape (N, T, H). - cache: Values needed in the backward pass """ h, cache = None, None ############################################################################## # TODO: Implement forward pass for a vanilla RNN running on a sequence of # # input data. You should use the rnn_step_forward function that you defined # # above. You can use a for loop to help compute the forward pass. # ############################################################################## N,T,D=x.shape H=b.shape[0] h=np.zeros((N,T,H)) prev_h=h0 cache=[] for t in range(T): xt=x[:,t,:] next_h,step_cache=rnn_step_forward(xt,prev_h,Wx,Wh,b) cache.append(step_cache) h[:,t,:]=next_h prev_h=next_h return h, cache def rnn_backward(dh, cache): """ Compute the backward pass for a vanilla RNN over an entire sequence of data. Inputs: - dh: Upstream gradients of all hidden states, of shape (N, T, H) Returns a tuple of: - dx: Gradient of inputs, of shape (N, T, D) - dh0: Gradient of initial hidden state, of shape (N, H) - dWx: Gradient of input-to-hidden weights, of shape (D, H) - dWh: Gradient of hidden-to-hidden weights, of shape (H, H) - db: Gradient of biases, of shape (H,) """ dx, dh0, dWx, dWh, db = None, None, None, None, None ############################################################################## # TODO: Implement the backward pass for a vanilla RNN running an entire # # sequence of data. You should use the rnn_step_backward function that you # # defined above. You can use a for loop to help compute the backward pass. # ############################################################################## N,T,H=dh.shape D=cache[0][0].shape[1] dprev_h=np.zeros((N,H)) dx=np.zeros((N,T,D)) dWx=np.zeros((D,H)) dWh=np.zeros((H,H)) db=np.zeros((H,)) for t in range(T): t=T-1-t dx[:,t,:], dprev_h, dWxt, dWht, dbt=rnn_step_backward(dh[:,t,:]+dprev_h,cache[t]) dWx, dWh, db = dWx+dWxt, dWh+dWht, db+dbt dh0=dprev_h return dx, dh0, dWx, dWh, db def word_embedding_forward(x, W): """ Forward pass for word embeddings. We operate on minibatches of size N where each sequence has length T. We assume a vocabulary of V words, assigning each to a vector of dimension D. Inputs: - x: Integer array of shape (N, T) giving indices of words. Each element idx of x muxt be in the range 0 <= idx < V. - W: Weight matrix of shape (V, D) giving word vectors for all words. Returns a tuple of: - out: Array of shape (N, T, D) giving word vectors for all input words. - cache: Values needed for the backward pass """ out, cache = None, None ############################################################################## # TODO: Implement the forward pass for word embeddings. # N,T=x.shape V,D=W.shape out=np.zeros((N,T,D)) for i in range(N): for j in range(T): out[i,j]=W[x[i,j]] cache=(x,W.shape) return out, cache def word_embedding_backward(dout, cache): """ Backward pass for word embeddings. We cannot back-propagate into the words since they are integers, so we only return gradient for the word embedding matrix. HINT: Look up the function np.add.at Inputs: - dout: Upstream gradients of shape (N, T, D) - cache: Values from the forward pass Returns: - dW: Gradient of word embedding matrix, of shape (V, D). """ dW = None ############################################################################## # TODO: Implement the backward pass for word embeddings. # # # # Note that Words can appear more than once in a sequence. # # HINT: Look up the function np.add.at # ############################################################################## x,W_shape=cache dW=np.zeros(W_shape) np.add.at(dW,x,dout) return dW def sigmoid(x): """ A numerically stable version of the logistic sigmoid function. """ pos_mask = (x >= 0) neg_mask = (x < 0) z = np.zeros_like(x) z[pos_mask] = np.exp(-x[pos_mask]) z[neg_mask] = np.exp(x[neg_mask]) top = np.ones_like(x) top[neg_mask] = z[neg_mask] return top / (1 + z) def temporal_affine_forward(x, w, b): """ Forward pass for a temporal affine layer. The input is a set of D-dimensional vectors arranged into a minibatch of N timeseries, each of length T. We use an affine function to transform each of those vectors into a new vector of dimension M. Inputs: - x: Input data of shape (N, T, D) - w: Weights of shape (D, M) - b: Biases of shape (M,) Returns a tuple of: - out: Output data of shape (N, T, M) - cache: Values needed for the backward pass """ N, T, D = x.shape M = b.shape[0] out = x.reshape(N * T, D).dot(w).reshape(N, T, M) + b cache = x, w, b, out return out, cache def temporal_affine_backward(dout, cache): """ Backward pass for temporal affine layer. Input: - dout: Upstream gradients of shape (N, T, M) - cache: Values from forward pass Returns a tuple of: - dx: Gradient of input, of shape (N, T, D) - dw: Gradient of weights, of shape (D, M) - db: Gradient of biases, of shape (M,) """ x, w, b, out = cache N, T, D = x.shape M = b.shape[0] dx = dout.reshape(N * T, M).dot(w.T).reshape(N, T, D) dw = dout.reshape(N * T, M).T.dot(x.reshape(N * T, D)).T db = dout.sum(axis=(0, 1)) return dx, dw, db def temporal_softmax_loss(x, y, mask, verbose=False): """ A temporal version of softmax loss for use in RNNs. We assume that we are making predictions over a vocabulary of size V for each timestep of a timeseries of length T, over a minibatch of size N. The input x gives scores for all vocabulary elements at all timesteps, and y gives the indices of the ground-truth element at each timestep. We use a cross-entropy loss at each timestep, summing the loss over all timesteps and averaging across the minibatch. As an additional complication, we may want to ignore the model output at some timesteps, since sequences of different length may have been combined into a minibatch and padded with NULL tokens. The optional mask argument tells us which elements should contribute to the loss. Inputs: - x: Input scores, of shape (N, T, V) - y: Ground-truth indices, of shape (N, T) where each element is in the range 0 <= y[i, t] < V - mask: Boolean array of shape (N, T) where mask[i, t] tells whether or not the scores at x[i, t] should contribute to the loss. Returns a tuple of: - loss: Scalar giving loss - dx: Gradient of loss with respect to scores x. """ N, T, V = x.shape x_flat = x.reshape(N * T, V) y_flat = y.reshape(N * T) mask_flat = mask.reshape(N * T) probs = np.exp(x_flat - np.max(x_flat, axis=1, keepdims=True)) probs /= np.sum(probs, axis=1, keepdims=True) loss = -np.sum(mask_flat * np.log(probs[np.arange(N * T), y_flat])) / N dx_flat = probs.copy() dx_flat[np.arange(N * T), y_flat] -= 1 dx_flat /= N dx_flat *= mask_flat[:, None] if verbose: print('dx_flat: ', dx_flat.shape) dx = dx_flat.reshape(N, T, V) return loss, dx
import numpy as np from cs231n import optim from cs231n.coco_utils import sample_coco_minibatch class CaptioningSolver(object): """基于RNN结构的训练过程""" def __init__(self,model,data,**kwargs): """ 必选参数: - model: 符合一定要求的model - data: 特定格式的训练和验证数据 可选参数: - update_rule: 可选梯度下降方法,默认sgd - optim_config: 梯度下降的参数 - lr_decay: 学习率衰减参数,各个epoch更新lr_decay=lr*lr_decay.默认不衰减,即1.0 - batch_size: 批大小 - num_epochs: 训练的epoch数量 - print_every: 几个epochs打印一次信息,默认一个. - verbose: 训练过程中是否打印信息 """ self.model=model self.data=data self.update_rule=kwargs.pop('update_rule','sgd') self.optim_config=kwargs.pop('optim_config',{}) self.lr_decay=kwargs.pop('lr_decay',1.0) self.batch_size=kwargs.pop('batch_size',128) self.num_epochs=kwargs.pop('num_epochs',10) self.print_every=kwargs.pop('print_every',1) self.verbose=kwargs.pop('verbose',True) #有错误或者多余参数 报错 if len(kwargs)>0: extra=','.join('"%s"' % k for k in kwargs.keys()) raise ValueError('Unrecognized arguments %s'%extra) if not hasattr(optim,self.update_rule): raise ValueError('Invalid update rule %s' %self.update_rule) self.update_rule=getattr(optim,self.update_rule) self._reset() def _reset(self): #对一些重要变量的追踪 self.epoch=0 self.best_val_acc=0 self.best_paprams={} self.loss_history=[] self.train_acc_history=[] self.val_acc_history=[] #给每个权重矩阵都保存一份优化参数,有的方法如adam需要保存一些历史信息 #而每个参数矩阵的历史信息不一样,需要各自保存 self.optim_configs={} for p in self.model.params: d={k:v for k,v in self.optim_config.items()} self.optim_configs[p]=d def _step(self): ''' 单步更新参数,即一个迭代,只能被train()调用 ''' #获取小批量数据 minibatch=sample_coco_minibatch(self.data,batch_size=self.batch_size,split='train') captions,features,urls=minibatch #计算这批数据在现在参数下的loss和梯度 loss,grads=self.model.loss(features,captions) self.loss_history.append(loss) #更新参数 for p,w in self.model.params.items(): dw=grads[p] config=self.optim_configs[p] next_w,next_config=self.update_rule(w,dw,config) self.model.params[p]=next_w self.optim_configs[p]=next_config #计算正确率 def check_accuracy(self,X,y,num_samples=None,batch_size=128): N=X.shape[0] print(X.shape,y.shape) #如果num_sample不为空 则只从全部数据中选则num_sample个数据计算 if num_samples is not None and N>num_samples: mask=np.random.choice(N,num_samples) N=num_samples X=X[mask] y=y[mask] num_batches=N//batch_size if N%batch_size!=0: num_batches+=1 y_pred=[] for i in range(num_batches): start=i*batch_size end=(i+1)*batch_size y_pred.append(self.model.sample(X[start:end])) y_pred=np.concatenate(y_pred,axis=0) acc=np.mean(y_pred==y) return acc def train(self): ''' 自动训练全过程 ''' num_train=self.data['train_captions'].shape[0] iterations_pre_epoch=max(num_train//self.batch_size,1) num_iterations=self.num_epochs*iterations_pre_epoch for t in range(num_iterations): self._step() epoch_end=(t+1)%iterations_pre_epoch==0 if epoch_end: self.epoch+=1 for k in self.optim_configs: self.optim_configs[k]['learning_rate']*=self.lr_decay if(self.epoch%self.print_every==0): print ('(epoch %d / %d) loss: %f' % (self.epoch, self.num_epochs, self.loss_history[-1])) ''' first_it=(t==0) last_it=(t==num_iterations-1) if first_it or last_it or epoch_end: train_acc=self.check_accuracy(self.data['train_features'][self.data['train_image_idxs'] ],self.data['train_captions'],num_samples=1280) val_acc= self.check_accuracy(self.data['val_features'][self.data['val_image_idxs'] ],self.data['val_captions'],64) self.train_acc_history.append(train_acc) self.val_acc_history.append(val_acc) #可视化进度 if self.verbose: print ('(Epoch %d / %d) train acc: %f; val_acc: %f' % ( self.epoch, self.num_epochs, train_acc, val_acc)) #检查、保存模型 if val_acc>self.best_val_acc: self.best_val_acc=val_acc self.best_params={} for k,v in self.model.params.items(): self.best_params[k]=v.copy() '''
参考:https://blog.csdn.net/zhaojc1995/article/details/80572098
http://cs231n.github.io


