一、线性回归
线性回归是比较简单的机器学习算法，很多书籍介绍的第一种机器学习算法就是线性回归算法。线性回归平常容易忽视的三类问题，（1）线性回归的理论依据是什么，（2）过拟合意味着什么。（3）模型优化的方向。
1 线性回归的理论依据
泰勒公式
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，成立下式：
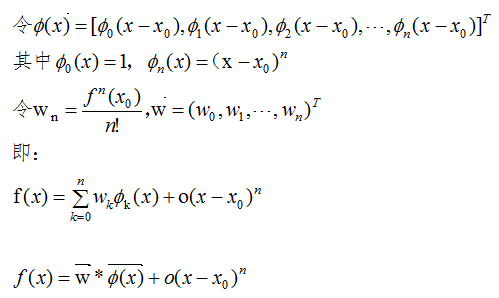
结论：对于区间[a,b]上任意一点，函数值都可以用两个向量内积的表达式近似，其中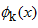
是基函数（basis function），
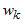是相应的系数。高阶表达式
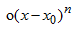表示两者值的误差。
傅里叶级数
周期函数f(x)可以用向量内积近似，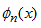
表示基函数，
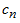表示相应的系数，
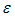表示误差
线性回归
由泰勒公式和傅里叶级数可知，当基函数的数量足够多时，向量内积无限接近于函数值。线性回归的向量内积表达式如下：
2 过拟合问题
构建模型的训练误差很小或为0，测试误差很大，这一现象称为过拟合。
高斯噪声数据模型
我们采集的样本数据其实包含了噪声，假设该噪声的高斯噪声模型，均值为0，方差为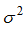
。若样本数据的标记为y1，理论标记为y，噪声为η，则有：
y1 = y + η，（其中，η是高斯分布的抽样）
上节的线性回归表达式的方差
表示的意义是噪声高斯分布的随机抽样，书本的线性回归表达式把方差
也包含进去了。
过拟合原因
数学术语：当基函数的个数足够大时，线性回归表达式的方程恒相等。
如下图
机器学习术语：模型太过复杂以致于把无关紧要的噪声也学进去了。
当线性回归的系数向量间差异比较大时，则大概率设计的模型处于过拟合了。用数学角度去考虑，若某个系数很大，对于相差很近的x值，结果会有较大的差异，这是较明显的过拟合现象。
过拟合的解决办法是降低复杂度。
3 模型的优化方向
模型的不同主要是体现在参数个数，参数大小以及正则化参数λ，优化模型的方法是调节上面三个参数（但不仅限于此，如核函数），目的是找到最优模型。
通过泰勒公式和傅里叶级数的例子说明线性回归的合理性，线性回归表达式包含了方差项，该方差是高斯噪声模型的随机采样，若训练数据在线性回归的表达式恒相等，那么就要考虑过拟合问题了，回归系数间差异比较大也是判断过拟合的一种方式。模型优化的方法有很多种，比较常见的方法是调节参数个数，参数大小以及正则化参数λ。
参考链接：https://mp.weixin.qq.com/s/ANY0JBfaaP343pvQBxcUwQ
4 python代码实现
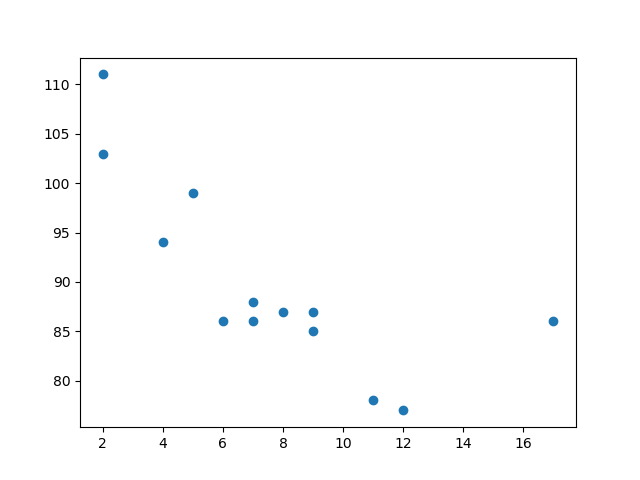
绘制散点图
import matplotlib.pyplot as plt x = [5,7,8,7,2,17,2,9,4,11,12,9,6] y = [99,86,87,88,111,86,103,87,94,78,77,85,86] plt.scatter(x, y) plt.show()
结果：
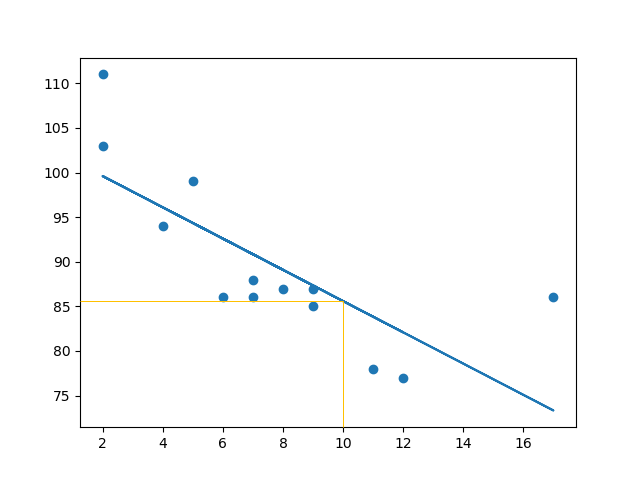
2 导入 scipy 并绘制线性回归线：
import matplotlib.pyplot as plt from scipy import stats x = [5,7,8,7,2,17,2,9,4,11,12,9,6] y = [99,86,87,88,111,86,103,87,94,78,77,85,86] slope, intercept, r, p, std_err = stats.linregress(x, y) def myfunc(x): return slope * x + intercept mymodel = list(map(myfunc, x)) plt.scatter(x, y) plt.plot(x, mymodel) plt.show()
结果：
二、多项式回归
如果数据点显然不适合线性回归（穿过数据点之间的直线），那么多项式回归可能是理想的选择。像线性回归一样，多项式回归使用变量 x 和 y 之间的关系来找到绘制数据点线的最佳方法。
1 绘制散点图
import matplotlib.pyplot as plt x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22] y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100] plt.scatter(x, y) plt.show()
结果：
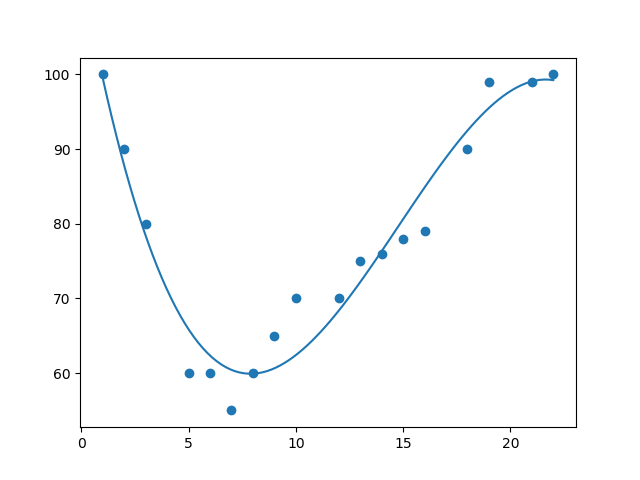
2 导入 numpy 和 matplotlib，然后画出多项式回归线：
import numpy import matplotlib.pyplot as plt x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22] y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100] mymodel = numpy.poly1d(numpy.polyfit(x, y, 3)) myline = numpy.linspace(1, 22, 100) plt.scatter(x, y) plt.plot(myline, mymodel(myline)) plt.show()
结果
R-Squared
重要的是要知道 x 轴和 y 轴的值之间的关系有多好，如果没有关系，则多项式回归不能用于预测任何东西。
该关系用一个称为 r 平方（ r-squared）的值来度量。
r 平方值的范围是 0 到 1，其中 0 表示不相关，而 1 表示 100％ 相关。
Python 和 Sklearn 模块将为您计算该值，您所要做的就是将 x 和 y 数组输入：
import numpy from sklearn.metrics import r2_score x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22] y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100] mymodel = numpy.poly1d(numpy.polyfit(x, y, 3)) print(r2_score(y, mymodel(x)))
三、多元回归
多元回归就像线性回归一样，但是具有多个独立值，这意味着我们试图基于两个或多个变量来预测一个值。
在 Python 中，我们拥有可以完成这项工作的模块。首先导入 Pandas 模块：
import pandas
Pandas 模块允许我们读取 csv 文件并返回一个 DataFrame 对象。
此文件仅用于测试目的，您可以在此处下载：cars.csv
df = pandas.read_csv("cars.csv")
然后列出独立值，并将这个变量命名为 X。
将相关值放入名为 y 的变量中。
X = df[['Weight', 'Volume']] y = df['CO2']
提示：通常，将独立值列表命名为大写 X，将相关值列表命名为小写 y。
我们将使用 sklearn 模块中的一些方法，因此我们也必须导入该模块：
from sklearn import linear_model
在 sklearn 模块中，我们将使用 LinearRegression() 方法创建一个线性回归对象。
该对象有一个名为 fit() 的方法，该方法将独立值和从属值作为参数，并用描述这种关系的数据填充回归对象：
regr = linear_model.LinearRegression()
regr.fit(X, y)
现在，我们有了一个回归对象，可以根据汽车的重量和排量预测 CO2 值：
# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量： predictedCO2 = regr.predict([[2300, 1300]])
完整实例：
import pandas from sklearn import linear_model df = pandas.read_csv("cars.csv") X = df[['Weight', 'Volume']] y = df['CO2'] regr = linear_model.LinearRegression() regr.fit(X, y) # 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量： predictedCO2 = regr.predict([[2300, 1300]]) print(predictedCO2)
打印回归对象系数值
import pandas from sklearn import linear_model df = pandas.read_csv("cars.csv") X = df[['Weight', 'Volume']] y = df['CO2'] regr = linear_model.LinearRegression() regr.fit(X, y) print(regr.coef_)
