#include <iostream>
#include <cstdio>
#include <cstring>
#define MAXN 40010
using namespace std ;
struct Graph
{
int vex , next , dis ;
};
Graph g[MAXN * 2] , Q[400];
int first[MAXN] , head[MAXN] , set[MAXN] , away[MAXN] , n , m ;
bool visited[MAXN] ;
//first[v]用来查找节点所在边,即g[first[v]],同时, g[i].next记录与节点v连接的节点,这俩个记录十分的关键,也就是这俩记录来实现深搜的
//head[v]用来查找该节点所在的询问的路径,和first[v]的作用类似,主要是为了在访问该节点的时候,将所有与该节点相邻或有关的已访问过的节点的询问路径的距离求出来
//away[v]用来记录节点v到根节点的距离
void Add (int v , int w , int d , int &j)
{
cout<<"v: "<<v<<" w: "<<w<<" d: "<<d<<" j: "<<j<<" ";
g[j].dis = d ;cout<<"g[j].dis: "<<g[j].dis<<" ";
g[j].vex = w ;cout<<"g[j].vex: "<<g[j].vex<<" ";
g[j].next = first[v] ;cout<<"g[j].next: "<<g[j].next<<" "; //记录与v相邻的路径
first[v] = j++;cout<<"first[v]: "<<first[v]<<endl;
}
void Add2 (int v , int w , int &j)
{
Q[j].dis = -1 ; //未计算过,初始化为-1
Q[j].vex = w ;
Q[j].next = head[v] ;
head[v] = j ++ ;
}
void Read ()
{
int i , j , v , w , d ;
memset (first , -1 , sizeof (first)) ;
memset (head , -1 , sizeof (head)) ;
memset (visited , false , sizeof (visited)) ;
//初始化是肯定要的
scanf ("%d%d" , &n , &m) ;
for (j = 0 , i = 1 ; i < n ; i ++)//j从0 开始
{
scanf ("%d%d%d" , &v , &w , &d) ;
Add (v , w , d , j) ;
Add (w , v , d , j) ;
//这里进行俩次记录,主要是为下面记录的俩次询问路径做准备
}
for (i = j = 0 ; i < m ; i ++)
{
scanf ("%d%d" , &v , &w) ;
Add2 (v , w , j) ;
Add2 (w , v , j) ;
//这里用进行俩次记录,首先,v到w和w到v的距离是一样的,其次,
//因为在访问到v的时候,w可能还没访问到,如果没进行俩次记录的话,当访问到w时,则也不会计算v和w的距离
//当然,记录俩次,但只会计算一次
}
}
int Find (int x)
{
if (x != set[x])
set[x] = Find (set[x]) ;
return set[x] ;
} //查找父节点,同时路径压缩
void DFS (int v , int dis)
{
int i ;
set[v] = v ;
visited[v] = true ;
away[v] = dis ;
printf("访问节点%d\n",v);
for (i = head[v] ; i != -1 ; i = Q[i].next)
{
printf("q[i].next为%d\n",Q[i].next);
if (visited[Q[i].vex])
{
printf("计算节点%d和%d的距离\n",v,Q[i].vex);
Q[i].dis = away[v] + away[Q[i].vex] - 2 * away[Find (set[Q[i].vex])] ;
//这步计算很好理解,关键是确定了Find(set[Q[i].vex)就是v和Q[i].vex的最近公共祖先
printf("此时%d 的父节点为%d ,%d的父节点为%d\n",v,set[v],Q[i].vex,Find(set[Q[i].vex]));
printf("away[v] :%d ,away[q[i].vex]: %d ,away[Find(set[q[i].vex])]:%d \n",away[v],away[Q[i].vex],away[Find(set[Q[i].vex])]);
}
}
for (i = first[v] ; i != -1 ; i = g[i].next)
{
printf("i为:%d g[i].vex为: %d v为: %d first[v]为: %d g[i].next为: %d 节点%d 是否已查: %d\n",i,g[i].vex,v,first[v],g[i].next,g[i].vex,visited[g[i].vex]);
if (!visited[g[i].vex])
{
printf("进入递归\n");
DFS (g[i].vex , dis + g[i].dis) ; //注意这里的距离累加 dis + g[i].dis,因为这一步的累加,所以,away[g[i].vex]就记录了该节点到根节点的距离
set[g[i].vex] = v ; //这一步十分重要,当v的某一子树访问完了,才将子树连接到节点v上
printf("退出一个递归,此时%d的父节点为%d\n",g[i].vex,set[g[i].vex]);
}
}
}
void Print ()
{
int i , j ;
for (i = j = 0 ; i < m ; i ++ , j += 2)
if (Q[j].dis != -1)
printf ("%d\n" , Q[j].dis) ;
else
printf ("%d\n" , Q[j + 1].dis) ; //这里的话,因为这些边都重复的插入,都一条边只会被访问一次,所以俩者必有一个
}
int main ()
{
int t ;
scanf ("%d" , &t) ;
while (t --)
{
Read () ;
DFS (1 , 0) ;
Print () ;
}
return 0 ;
}
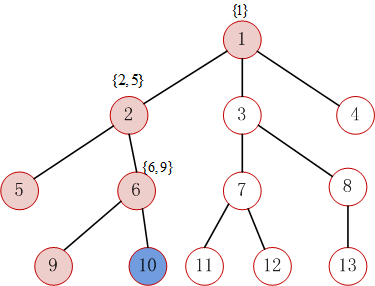
代码调试显示
1
13 1
1 2 1
1 3 1
1 4 1
2 5 1
2 6 1
3 7 1
3 8 1
6 9 1
6 10 1
7 11 1
7 12 1
8 13 1
11 13
1
13 1
1 2 1
v: 1 w: 2 d: 1 j: 0 g[j].dis: 1 g[j].vex: 2 g[j].next: -1 first[v]: 0
v: 2 w: 1 d: 1 j: 1 g[j].dis: 1 g[j].vex: 1 g[j].next: -1 first[v]: 1
1 3 1
v: 1 w: 3 d: 1 j: 2 g[j].dis: 1 g[j].vex: 3 g[j].next: 0 first[v]: 2
v: 3 w: 1 d: 1 j: 3 g[j].dis: 1 g[j].vex: 1 g[j].next: -1 first[v]: 3
1 4 1
v: 1 w: 4 d: 1 j: 4 g[j].dis: 1 g[j].vex: 4 g[j].next: 2 first[v]: 4
v: 4 w: 1 d: 1 j: 5 g[j].dis: 1 g[j].vex: 1 g[j].next: -1 first[v]: 5
2 5 1
v: 2 w: 5 d: 1 j: 6 g[j].dis: 1 g[j].vex: 5 g[j].next: 1 first[v]: 6
v: 5 w: 2 d: 1 j: 7 g[j].dis: 1 g[j].vex: 2 g[j].next: -1 first[v]: 7
2 6 1
v: 2 w: 6 d: 1 j: 8 g[j].dis: 1 g[j].vex: 6 g[j].next: 6 first[v]: 8
v: 6 w: 2 d: 1 j: 9 g[j].dis: 1 g[j].vex: 2 g[j].next: -1 first[v]: 9
3 7 1
v: 3 w: 7 d: 1 j: 10 g[j].dis: 1 g[j].vex: 7 g[j].next: 3 first[v]: 10
v: 7 w: 3 d: 1 j: 11 g[j].dis: 1 g[j].vex: 3 g[j].next: -1 first[v]: 11
3 8 1
v: 3 w: 8 d: 1 j: 12 g[j].dis: 1 g[j].vex: 8 g[j].next: 10 first[v]: 12
v: 8 w: 3 d: 1 j: 13 g[j].dis: 1 g[j].vex: 3 g[j].next: -1 first[v]: 13
6 9 1
v: 6 w: 9 d: 1 j: 14 g[j].dis: 1 g[j].vex: 9 g[j].next: 9 first[v]: 14
v: 9 w: 6 d: 1 j: 15 g[j].dis: 1 g[j].vex: 6 g[j].next: -1 first[v]: 15
6 10 1
v: 6 w: 10 d: 1 j: 16 g[j].dis: 1 g[j].vex: 10 g[j].next: 14 first[v]: 16
v: 10 w: 6 d: 1 j: 17 g[j].dis: 1 g[j].vex: 6 g[j].next: -1 first[v]: 17
7 11 1
v: 7 w: 11 d: 1 j: 18 g[j].dis: 1 g[j].vex: 11 g[j].next: 11 first[v]: 18
v: 11 w: 7 d: 1 j: 19 g[j].dis: 1 g[j].vex: 7 g[j].next: -1 first[v]: 19
7 12 1
v: 7 w: 12 d: 1 j: 20 g[j].dis: 1 g[j].vex: 12 g[j].next: 18 first[v]: 20
v: 12 w: 7 d: 1 j: 21 g[j].dis: 1 g[j].vex: 7 g[j].next: -1 first[v]: 21
8 13 1
v: 8 w: 13 d: 1 j: 22 g[j].dis: 1 g[j].vex: 13 g[j].next: 13 first[v]: 22
v: 13 w: 8 d: 1 j: 23 g[j].dis: 1 g[j].vex: 8 g[j].next: -1 first[v]: 23
11 13
访问节点1
i为:4 g[i].vex为: 4 v为: 1 first[v]为: 4 g[i].next为: 2 节点4 是否已查: 0
进入递归
访问节点4
i为:5 g[i].vex为: 1 v为: 4 first[v]为: 5 g[i].next为: -1 节点1 是否已查: 1
退出一个递归,此时4的父节点为1
i为:2 g[i].vex为: 3 v为: 1 first[v]为: 4 g[i].next为: 0 节点3 是否已查: 0
进入递归
访问节点3
i为:12 g[i].vex为: 8 v为: 3 first[v]为: 12 g[i].next为: 10 节点8 是否已查:
0
进入递归
访问节点8
i为:22 g[i].vex为: 13 v为: 8 first[v]为: 22 g[i].next为: 13 节点13 是否已查
: 0
进入递归
访问节点13
q[i].next为-1
i为:23 g[i].vex为: 8 v为: 13 first[v]为: 23 g[i].next为: -1 节点8 是否已查
: 1
退出一个递归,此时13的父节点为8
i为:13 g[i].vex为: 3 v为: 8 first[v]为: 22 g[i].next为: -1 节点3 是否已查:
1
退出一个递归,此时8的父节点为3
i为:10 g[i].vex为: 7 v为: 3 first[v]为: 12 g[i].next为: 3 节点7 是否已查:
0
进入递归
访问节点7
i为:20 g[i].vex为: 12 v为: 7 first[v]为: 20 g[i].next为: 18 节点12 是否已查
: 0
进入递归
访问节点12
i为:21 g[i].vex为: 7 v为: 12 first[v]为: 21 g[i].next为: -1 节点7 是否已查
: 1
退出一个递归,此时12的父节点为7
i为:18 g[i].vex为: 11 v为: 7 first[v]为: 20 g[i].next为: 11 节点11 是否已查
: 0
进入递归
访问节点11
q[i].next为-1
计算节点11和13的距离
此时11 的父节点为11 ,13的父节点为3
away[v] :3 ,away[q[i].vex]: 3 ,away[Find(set[q[i].vex])]:1
i为:19 g[i].vex为: 7 v为: 11 first[v]为: 19 g[i].next为: -1 节点7 是否已查
: 1
退出一个递归,此时11的父节点为7
i为:11 g[i].vex为: 3 v为: 7 first[v]为: 20 g[i].next为: -1 节点3 是否已查:
1
退出一个递归,此时7的父节点为3
i为:3 g[i].vex为: 1 v为: 3 first[v]为: 12 g[i].next为: -1 节点1 是否已查:
1
退出一个递归,此时3的父节点为1
i为:0 g[i].vex为: 2 v为: 1 first[v]为: 4 g[i].next为: -1 节点2 是否已查: 0
进入递归
访问节点2
i为:8 g[i].vex为: 6 v为: 2 first[v]为: 8 g[i].next为: 6 节点6 是否已查: 0
进入递归
访问节点6
i为:16 g[i].vex为: 10 v为: 6 first[v]为: 16 g[i].next为: 14 节点10 是否已查
: 0
进入递归
访问节点10
i为:17 g[i].vex为: 6 v为: 10 first[v]为: 17 g[i].next为: -1 节点6 是否已查
: 1
退出一个递归,此时10的父节点为6
i为:14 g[i].vex为: 9 v为: 6 first[v]为: 16 g[i].next为: 9 节点9 是否已查:
0
进入递归
访问节点9
i为:15 g[i].vex为: 6 v为: 9 first[v]为: 15 g[i].next为: -1 节点6 是否已查:
1
退出一个递归,此时9的父节点为6
i为:9 g[i].vex为: 2 v为: 6 first[v]为: 16 g[i].next为: -1 节点2 是否已查:
1
退出一个递归,此时6的父节点为2
i为:6 g[i].vex为: 5 v为: 2 first[v]为: 8 g[i].next为: 1 节点5 是否已查: 0
进入递归
访问节点5
i为:7 g[i].vex为: 2 v为: 5 first[v]为: 7 g[i].next为: -1 节点2 是否已查: 1
退出一个递归,此时5的父节点为2
i为:1 g[i].vex为: 1 v为: 2 first[v]为: 8 g[i].next为: -1 节点1 是否已查: 1
退出一个递归,此时2的父节点为1
4
Process returned 0 (0x0) execution time : 2.699 s
Press any key to continue.




