CF1550C Manhattan Subarrays

题面

对于平面上的两点 \(p(x_p,y_p),q(x_q,y_q)\) ，我们定义它们之间的曼哈顿距离 \(d(p,q)=|x_p-x_q|+|y_p-y_q|\) 。进一步定义由三个点构成的一组点 \(p,q,r\) 是坏的仅当 \(d(p,r)=d(p,q)+d(q,r)\) 。

我们定义序列 \(b\) 是好的仅当无法选出一组互不相同的整数 \(i,j,k\) 使得 \((b_i,i),(b_j,j),(b_k,k)\) 这组点是坏的。

给定长度为 \(n\) 的序列 \(a\)，求 \(a\) 有多少个子段是好的。 \(T\) 组数据。

分析

在什么情况下三元组 \((p,q,r)\) 是坏的？假设 \(y_p\leq y_q\leq y_r\) ，根据曼哈顿距离的定义（看图也行），当 点 \(q\) 在区间点 \([p,r]\) 中时，这个三元组是坏的。

图：

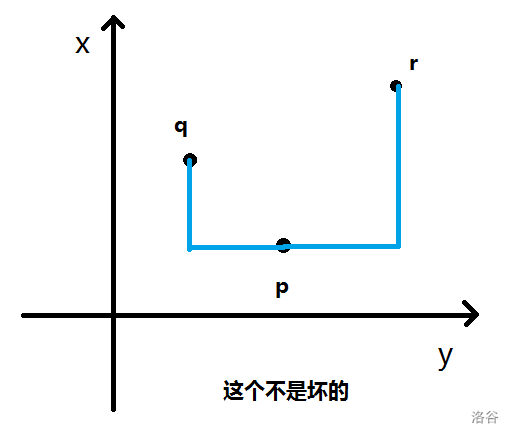
证明图：

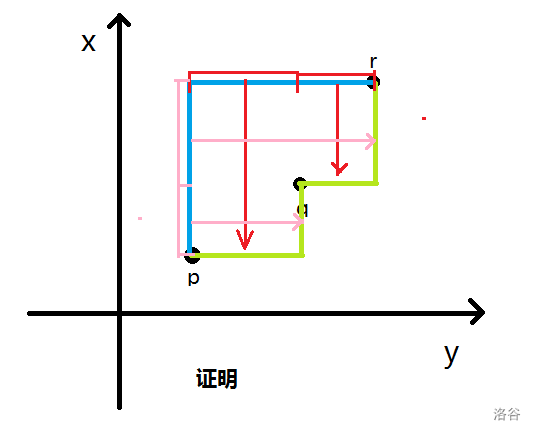
回到序列 \(a\) ,选出 \(i,j,k\) 来，此时为 \(p(a_i,i),q(a_j,j),r(a_k,k)\) ,若 \(i<j<k\) ，并且 \(a_i\leq a_j\leq a_k\) 或者 \(a_i\geq a_j\geq a_k\) 时，符合上图1情况（三元组是坏的）。

以上情况总结出：对序列 \(a\) 的一个子段不能够找出一个三元组是单调递增或单调递减的，此子段是好的。

下面，我们对子段的长度分情况讨论：

1.子段为长度为 \(1\) 时，\(a\) 序列中好的字段有 \(n\) 个。

2.子段为长度为 \(2\) 时，\(a\) 序列中好的字段有 \(n-1\) 个。

3.子段为长度为 \(3\) 或 \(4\) 时，直接暴力枚举 \(a\) 序列中的每一个三元组。

4.子段为长度为 \(\geq 5\) 时，\(a\) 序列中没有好的字段，因为，一个长度 \(\geq 5\) 的区间的单调不减（增）子序列的长度 \(\geq 3\) 。

上代码：

#include<bits/stdc++.h>
using  namespace std;
int t,n,sum;
int a[200005];
bool cyl_ak_ioi(int a,int b,int c){//判断递增还是递减 
	if((a<=b&&b<=c)||(a>=b&&b>=c))
		return 0;
	else
		return 1;
}
int main(){
	cin>>t;
	while(t--){
		cin>>n;
		for(int i=1;i<=n;i++)
			cin>>a[i];
		sum=n*2-1;//一、二种情况 
		for(int i=1;i<=n-2;i++)//第三种情况 
			if(cyl_ak_ioi(a[i],a[i+1],a[i+2]))
				sum++;
		for(int i=1;i<=n-3;i++)//第四种情况 
			if(cyl_ak_ioi(a[i],a[i+1],a[i+2])&&cyl_ak_ioi(a[i],a[i+1],a[i+3])&&cyl_ak_ioi(a[i],a[i+2],a[i+3])&&cyl_ak_ioi(a[i+1],a[i+2],a[i+3]))
			//有些暴力，大家凑活着看吧 XD 
				sum++;
		cout<<sum<<"\n";
	}
	return 0;
}