[b0044] numpy_快速上手

 1 概念理清

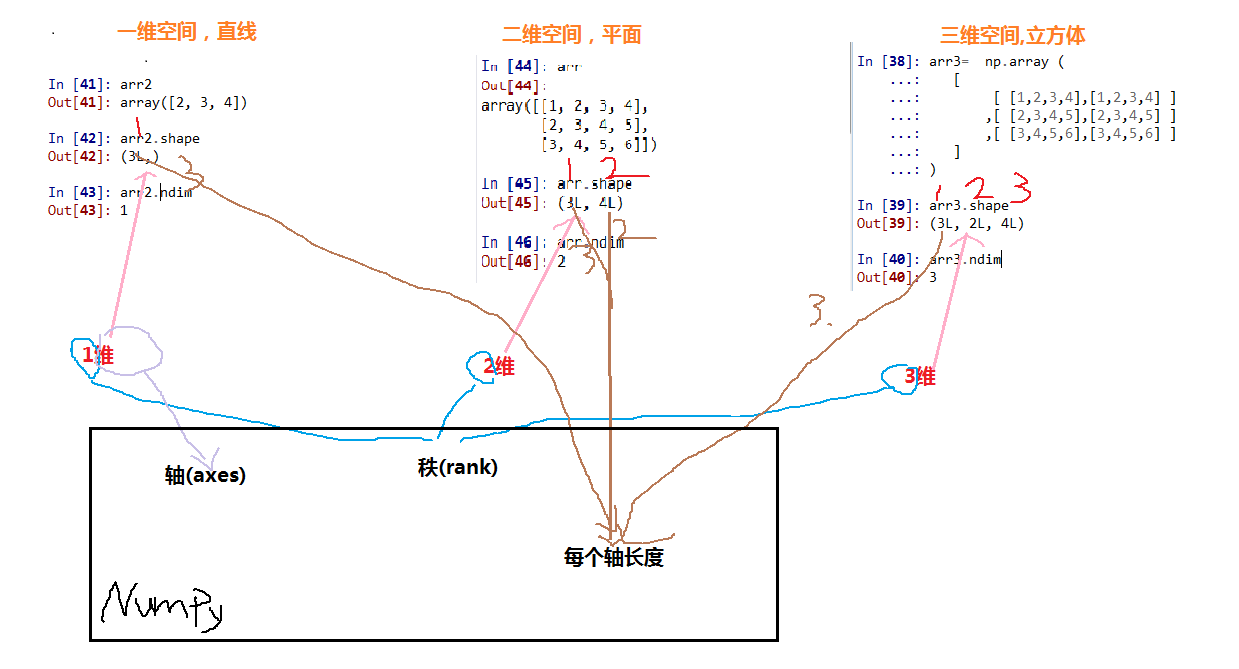
 2 创建数组

2.1 

f1= np.array(
[
[1,2,3,4],
[2,3,4,5],
[3,4,5,6]
]
)

 其他代码

a= np.array([
    [
        [3.4,5,6,8],
        [3,2.4,5,7]
    ],
    [    [2.3,4,5,6],
        [0.9,5,6,1]
    ],
    [
        [9,6.7,3,2],
        [1,3,4,5]
    ]
 ])
 
 
b = np.array((
    (
        (1,2,3,4),(4,5,6,7),(9,3,4,5)
    ),
    (
        (0,2,3,4),(4,5,6,7),(4,5,2,3)
    )
))

 

2.2

• zeros
• empty
• ones 
• eye

 

# 零矩阵
In [49]: f2 = zeros( (3,4) )

In [50]: f2
Out[50]: 
array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.]])

# 单位矩阵
In [51]: eye(3)
Out[51]: 
array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

 

2.3

2.3.1 arange

f3 = arange(15).reshape(3,5)   

注:

numpy.arange  指向同一个内存空间

>>> arange(15)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])

>>> arange( 10, 30, 5 )

array([10, 15, 20, 25])

 

2.3.2 linspace 

# linspace 等差序列， (开始,结束,元素个数)
In [154]: linspace(2,12,3)
Out[154]: array([ 2., 7., 12.]

 

2.3.3 logspace 

# logspace 等比数列， (开始,结束,元素个数)
* 第一个数 10^2
* 第二个数 10^12
In [155]: logspace(2,12,3)
Out[155]: array([ 1.00000000e+02, 1.00000000e+07, 1.00000000e+12])

 

2.3.4 random

#random 函数
In [177]: np.random.random()

In [178]: np.random.random((2,3,4))
Out[178]:
array([[[ 0.05126289, 0.66402449, 0.22970131, 0.73774777],
[ 0.72501932, 0.20642975, 0.38318838, 0.70826703],
[ 0.86349343, 0.34179916, 0.32829582, 0.55624637]],

[[ 0.59645461, 0.83145358, 0.85956141, 0.81924494],
[ 0.01116166, 0.71089623, 0.91432385, 0.66226528],
[ 0.5791923 , 0.42764113, 0.56575513, 0.54864404]]])

 

In [182]: np.random.random_sample((2,3))
Out[182]:
array([[ 0.3591195 , 0.89974204, 0.20622608],
[ 0.64718978, 0.24135722, 0.44665569]])

 

 

其它函数array, zeros, zeros_like, ones, ones_like, empty, empty_like, arange, linspace, rand, randn, fromfunction, fromfile参考：NumPy示例

 

3 索引，切片和迭代

 

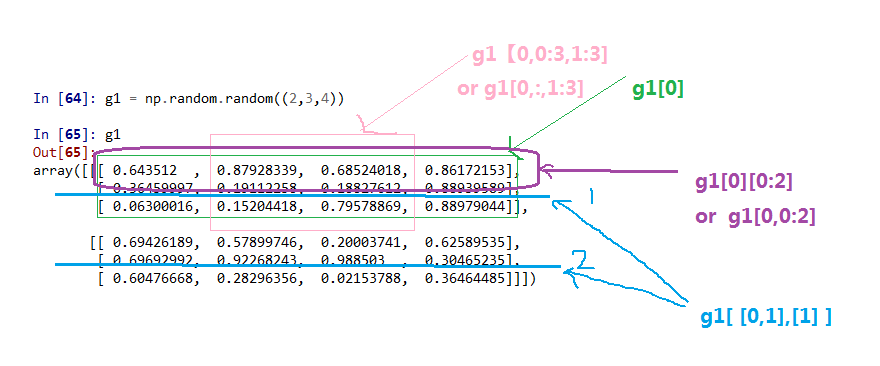
4 基本运算

In [106]: a = array( [20,30,40,50] )

In [107]: b = arange( 4 )

In [108]: b
Out[108]: array([0, 1, 2, 3])

In [109]: c = a-b

In [110]: c
Out[110]: array([20, 29, 38, 47])

In [111]: b**2
Out[111]: array([0, 1, 4, 9])

In [112]: 10*sin(a)
Out[112]: array([ 9.12945251, -9.88031624,  7.4511316 , -2.62374854])

In [113]: a<35
Out[113]: array([ True,  True, False, False], dtype=bool)

In [114]: b+3
Out[114]: array([3, 4, 5, 6]

  In [117]: b*3

  Out[117]: array([0, 3, 6, 9])

 

# 矩阵积 dot
第一个矩阵的列 = 第二个矩阵的行

(3*4) *  (4*5)  =  (3*5) 

In [115]: f1= np.array(
     ...:   [
     ...:     [1,2,3,4],
     ...:     [2,3,4,5],
     ...:     [3,4,5,6]
     ...:   ]
     ...: )
     ...: 
     ...: 
     ...: f2= np.array(
     ...:   [
     ...:     [1,2,3,4,1],
     ...:     [2,3,4,5,2],
     ...:     [3,4,5,6,3],
     ...:     [3,4,5,6,4]
     ...:   ]
     ...: )
     ...: 

In [116]: f1.dot(f2)
Out[116]: 
array([[26, 36, 46, 56, 30],
       [35, 49, 63, 77, 40],
       [44, 62, 80, 98, 50]])

 

行列式、秩、逆矩阵、转置

In [33]: a
Out[33]: 
array([[  3.,   2.,   3.],
       [  4.,   7.,   6.],
       [  7.,   8.,  11.]])

# 方阵
In [34]: a.shape
Out[34]: (3L, 3L)

# 求秩
In [35]: np.linalg.matrix_rank(a)
Out[35]: 3

# 求行列式

In [39]: np.linalg.det(a)
Out[39]: 32.0

# 求逆矩阵
In [40]: b = np.linalg.inv(a)

In [41]: b
Out[41]: 
array([[ 0.90625,  0.0625 , -0.28125],
       [-0.0625 ,  0.375  , -0.1875 ],
       [-0.53125, -0.3125 ,  0.40625]])

# 验证
In [42]: a.dot(b)
Out[42]: 
array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

# 转置
In [43]: a.T
Out[43]: 
array([[  3.,   4.,   7.],
       [  2.,   7.,   8.],
       [  3.,   6.,  11.]])

In [44]: a.transpose()
Out[44]: 
array([[  3.,   4.,   7.],
       [  2.,   7.,   8.],
       [  3.,   6.,  11.]])