a1n<复习> _算法理论-线性回归(转) _<还不错>_20190807
这是机器学习知识体系中的线性回归内容，完整的知识体系可以查看这里。
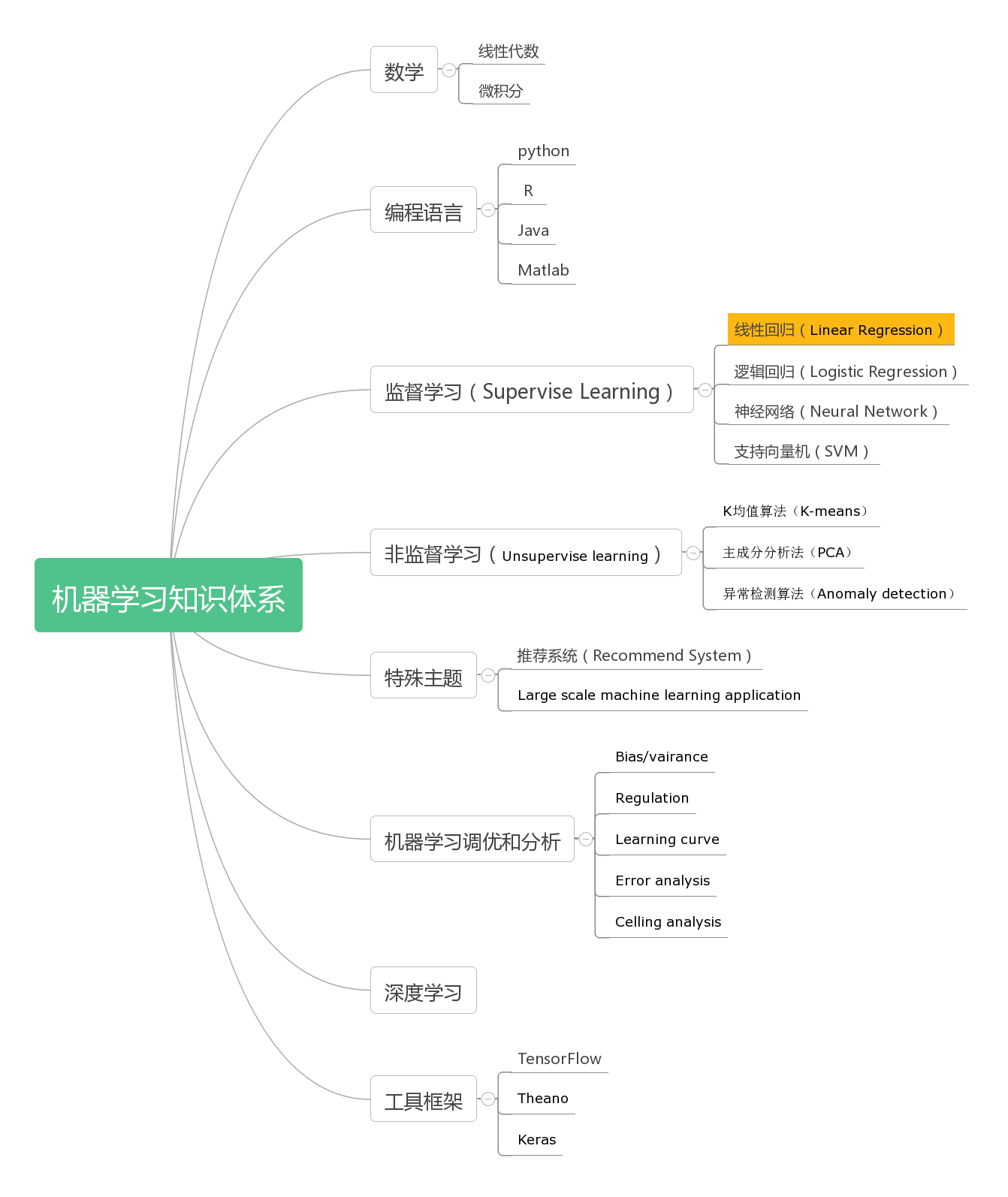
机器学习
什么是机器学习？业界有如下定义：
• ArthurSamuel(1959).MachineLearning:Fieldof study that gives computers the ability to learn without being explicitly programmed.
• TomMitchell(1998)Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
通常情况下，人类进行编程让机器完成一项工作，需要事先定义好一系列程序逻辑，机器然后根据编写的代码来执行，这种方式其实人类定义的规则，机器仅仅是运算执行而已。机器学习强调的是“without explicitly programmed”，通过机器根据某些经验数据，自我归纳总结算法，从而对一些新的数据进行准确的预测推导。
常见的应用场景包括：
1. 数据挖掘
2. 手写识别、自然语言处理（NLP）、计算机视觉
3. 产品推荐系统
4. ...
监督学习和无监督学习
机器学习方式大体上分为两种类别：监督学习和非监督学习。
监督学习指的是人类给机器一大堆标示(label)过的数据，通常指机器通过学习一系列(
, 
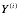)数据，X代表输入数据（特征Feature），Y代表输出数据，然后自我推导到X -> Y的公式，用于未来其他数据的预测判断使用。监督学习根据输出数据又分为回归问题（Regression）和分类问题（Classfication）。回归问题通常输出是一个连续的数值，分类问题的输出是几个特定的数值。
举例如下：
(a) 回归问题 - 给定一张人脸照片，估计出这个人的年龄（年龄输出是一个连续的数值）
(b) 分类问题 - 假定一个人患有肿瘤，判断是为恶性还是良性（恶性和良性的输出是几个特定的数值）
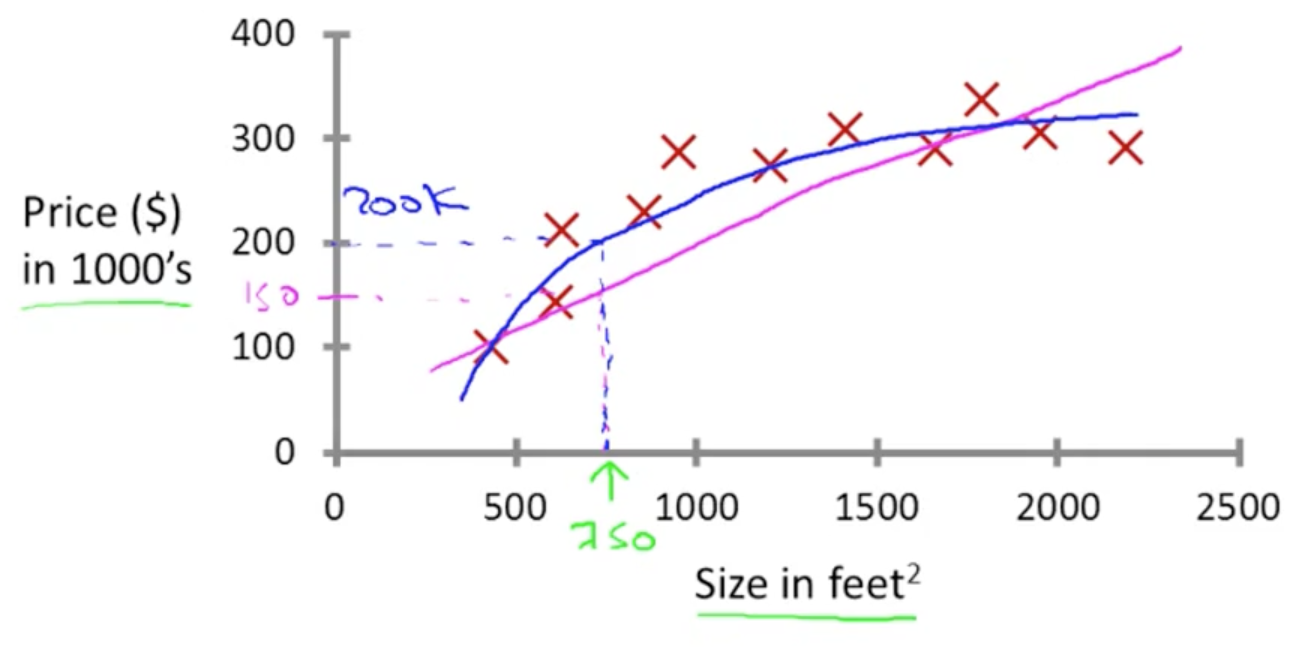
回归问题 - 房价预测
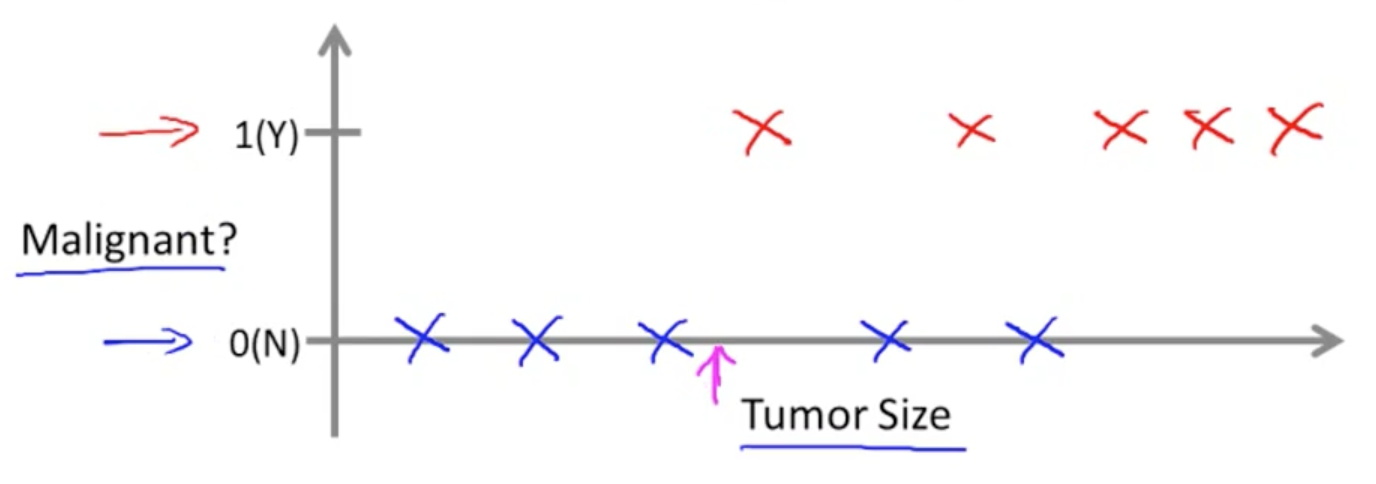
分类问题 - 肿瘤恶性/良性判断
无监督学习所学习的数据没有属性或标签这一概念 也就是说所有的数据都是一样的没有区别，通常给的数据是一系列(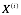
)，并不存在Y的输出数据。所以在无监督学习中，我们只有一个数据集，没人告诉我们该怎么做，我们也不知道每个数据点究竟是什么意思，相反它只告诉我们现在有一个数据集，你能在其中找到某种结构吗？对于给定的数据集，无监督学习算法可能判定，该数据集包含不同的聚类，并且能够归纳出哪些数据是一个聚类。
模型表达
在建立数学模型之前，先约定好一些表达形式：
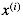- 代表输入数据 （features）
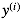- 代表输出数据（target）
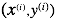- 代表一组训练数据（training example）
m - 代表训练数据的个数
n - 代表特征数量
监督学习目标就是，假定给一组训练数据，可以学习到一个函数方法h，可以使得h(x) -> y。这个函数方法h被称为假设（hypothesis）。整体流程如下：
代价函数
对于线性回归而言，函数h的表达式如下：
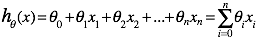
我们通常指定：
如果使用线性代数来表达的话
, 
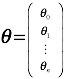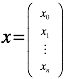
, 其中
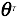是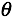
矩阵的转置（Transpose）。
那么对于一系列训练数据，如何获得最优的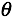
成为解决问题的核心。直观上而言，我们希望获取一组
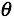值，使得h(x)越接近y越好。于是定义这个衡量标准为代价函数(Cost Function)如下：
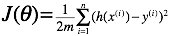
这个函数又称为Squared Error Function。
我们看下两个参数的Cost Function图像通常如下：
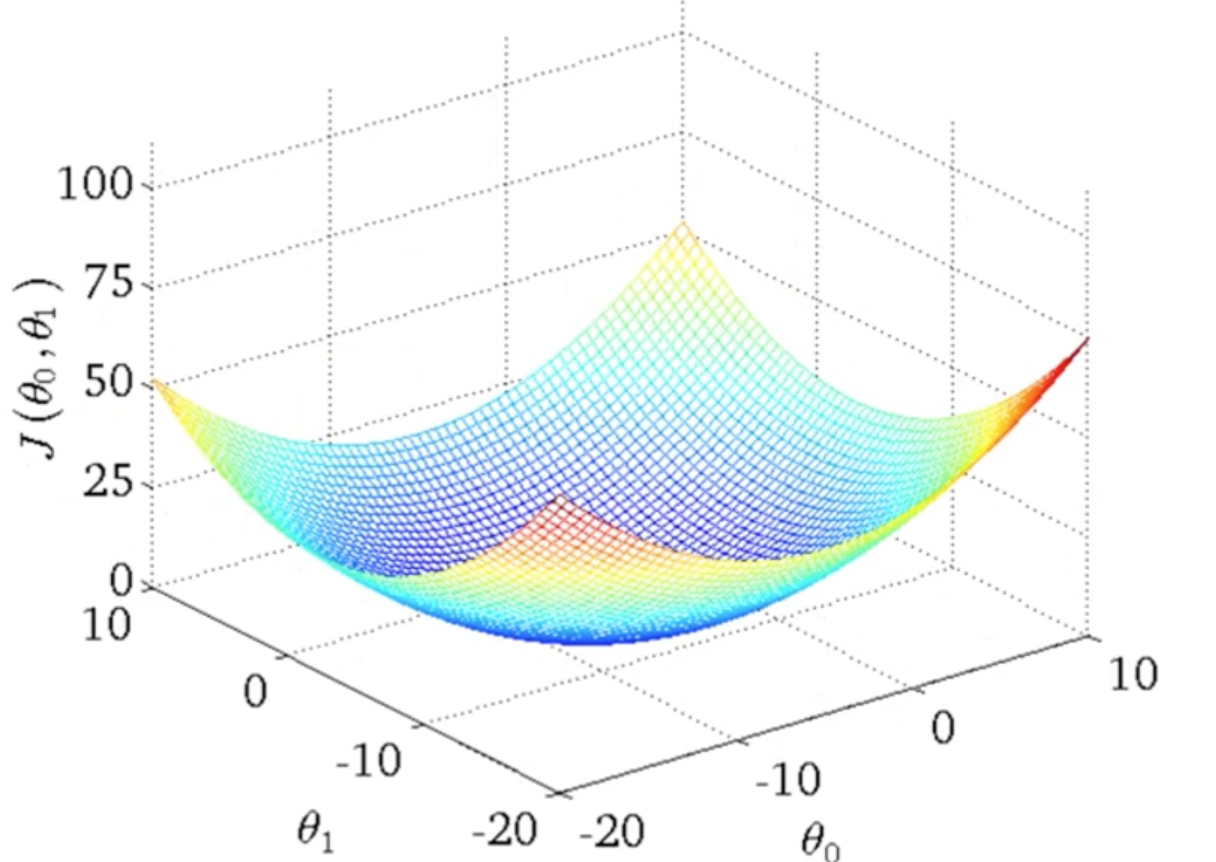
它是一个弓形的图像，这个弓形的最低点就是
的最优解。
梯度下降算法
对于线性回归问题，我们需要解决的事情往往如下：
定义出Cost Function - 
希望能够找到一组
，能够最小化，即
梯度下降算法步骤如下：
1. 随机选择一组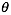
2. 不断的变化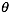
，让
变小
j=0,1,...n，
是所有n+1个值同时进行变化。α 是代表学习速率。
是Cost Function对的偏导数。
3. 直到寻找到最小值
偏导求解如下：
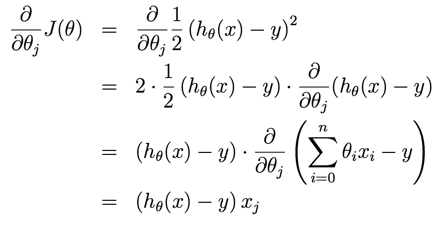
因此最终的梯度下降算法表达如下：
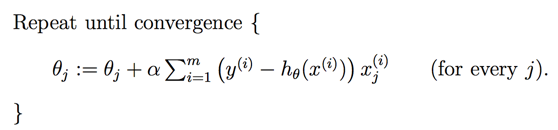
从Cost Function的图上，我们可以看到选择最优解的过程
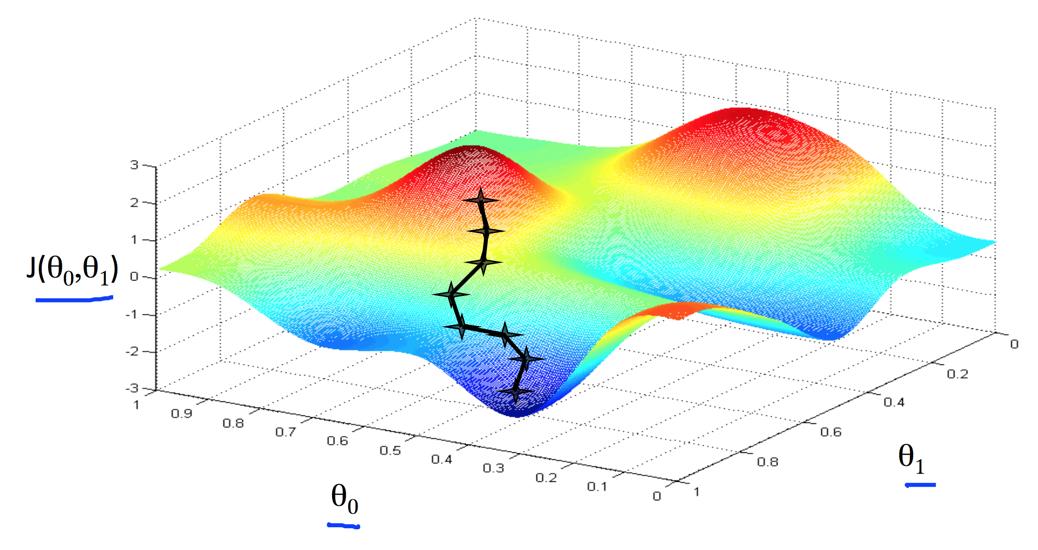
寻找到局部最优解1
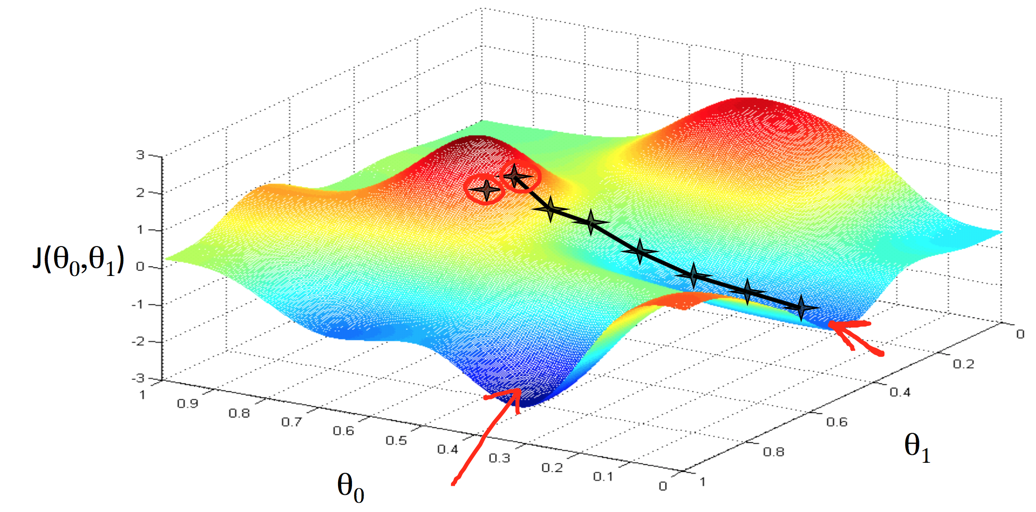
寻找到局部最优解2
从上面两个图可以看出，寻找最优解的过程很想是在下山，沿着下山的路下来，并最终到达一个局部的底部保持不变。
正规方程Normal Equation
梯度下降算法给出了一种方法可以最小化Cost Function。正规方程（Normal Equation）是另外一种方法，它使用非常直接的方式而不需要进行迭代的算法。在这个方法中，我们通过对J取对应的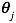
的偏导数，然后将偏导数设置为0。通过推导，正规方程如下：
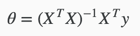
梯度下降算法和正规方程对比如下：
| 梯度下降算法 | 正规方程 |
| 需要选择学习速率参数 | 不需要学习速率参数 |
| 需要很多次迭代 | 不需要迭代 |
 |
 |
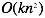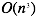| n如果很大依旧还能工作 | n如果很大，速度会非常慢 |
因此两种方法能否工作取决于n（特征x的数量）的大小，如果n很大（> 10000），那么使用梯度下降算法是比较明智的选择。
