Siamese Network介绍

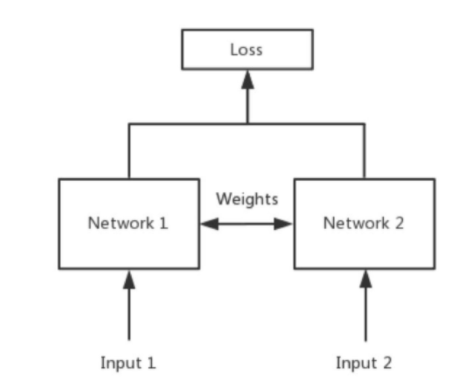
Siamese Network主要用于衡量两个输入的相似程度，如下图所示，Network 1和Network 2是共享权值的相同神经网络，这个网络将两个输入映射到新的特征空间中，通过设计好的与距离有关的损失函数来训练网络参数，使得训练好的网络可以衡量两个输入的相似程度。

Siamese Network经常用于要分类的类别很多或者不确定，但每个类别的样本比较少的情况，例如人脸识别。针对Siamese Network的训练可以设计多种不同的损失函数，本文介绍以下两种：

1. Triplet Loss. 以人脸识别为例，训练过程中的模型架构如下图所示：        

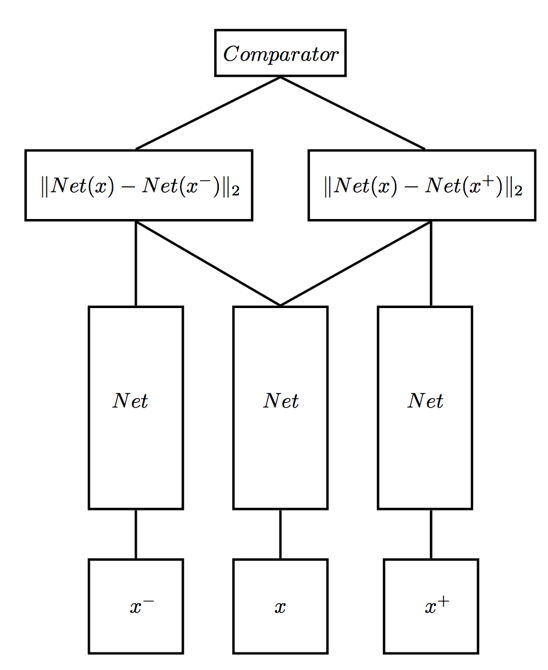在训练过程中每次同时输入三张人脸图片$(x, x^+, x^-)$，其中$x$和$x^+$为同一人，$x$和$x^-$为不同的人，损失函数的设计原理是使得网络输出$Net(x)$和$Net(x^+)$的距离很小，而$Net(x)$和$Net(x^-)$很大，Triplet Loss的形式可表示为：$$L(x, x^+, x^-) = \max \left(\|Net(x)-Net(x^+)\|_2^{2}-\|Net(x)-Net(x^-)\|_2^{2}+\alpha, 0\right)$$其中$\alpha$为一个预先给定的正值。

def triplet_loss(y_pred, alpha = 0.2):
    """
    Arguments:
    y_pred -- python list containing three objects:
            anchor -- the network output for the anchor images x, of shape (None, output_size)
            positive -- the network output for the positive images x+, of shape (None, output_size)
            negative -- the network output for the negative images x-, of shape (None, output_size)    
    Returns:
    loss -- real number, value of the loss
    """  
    anchor, positive, negative = y_pred[0], y_pred[1], y_pred[2]
    # Compute the (encoding) distance between the anchor and the positive
    pos_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, positive)), -1)
    # Compute the (encoding) distance between the anchor and the negative
    neg_dist = tf.reduce_sum(tf.square(tf.subtract(anchor, negative)), -1)
    # Subtract the two previous distances and add alpha.
    basic_loss = tf.add(tf.subtract(pos_dist,neg_dist), alpha)
    # Take the maximum of basic_loss and 0.0. Average over the training batch.
    loss = tf.reduce_mean(tf.maximum(basic_loss, 0.0), axis=None)
    return loss
Triplet Loss

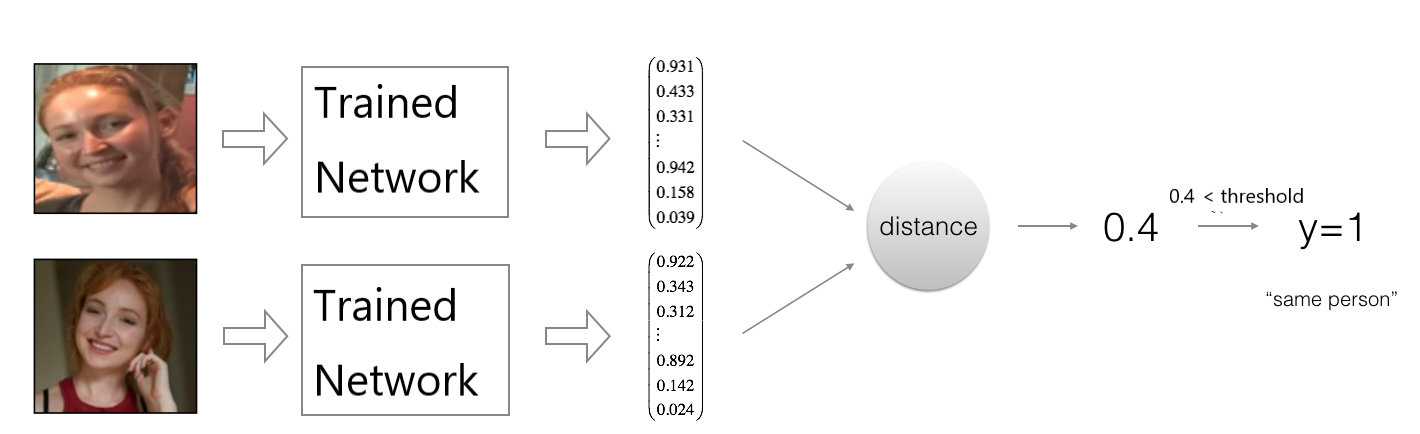
网络训练好之后，使用Siamese Network进行两个输入相似程度的判断。仍以人脸识别为例，对输入的两张人脸图片$x_1$和$x_2$计算距离$d(x_1,x_2)=\|Net(x_1)-Net(x_2)\|_2$，若距离小于预先给定的临界值threshold，则判断为同一人，否则为不同的人，如下图所示：

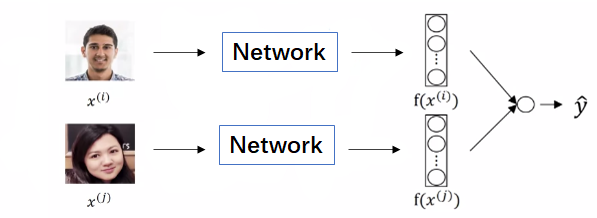
2. Binary Classification Loss. 如下图所示，在训练过程中每次输入两张图片$(x^{(i)},x^{(j)})$，从网络输出$f(x^{(i)}),f(x^{(j)})$后计算为同一人的概率$\hat{y}$：

$$\hat{y}=sigmoid\left(\sum_{k=1}^{output{\_size}} w_{k}\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|+b\right)$$若两张为同一人，则真实标签$y$为1，否则为0，使用Logistic回归中的交叉熵损失函数，即$$L(x^{(i)},x^{(j)})=L(\hat{y},y)=-y\ln\hat{y}-(1-y)\ln{(1-\hat{y})}$$训练结束后对输入的两张图片计算$\hat{y}$即可判断是否为同一人。

 

参考资料

posted on 2020-08-28 14:14  sunwq06  阅读(970)  评论(0)  编辑  收藏  举报

导航