Probabilistic PCA、Kernel PCA以及t-SNE
Probabilistic PCA
在之前的文章PCA与LDA介绍中介绍了PCA的基本原理,这一部分主要在此基础上进行扩展,在PCA中引入概率的元素,具体思路是对每个数据$\vec{x}_i$,假设$\vec{x}_{i} \sim N\left(W{\vec{z}_{i}}, \sigma^{2} I\right)$,其中$\vec{z}_{i}$是一个低维向量,它的先验分布满足$\vec{z}_{i} \sim N(0, I)$,$W$以及所有的$\vec{z}_i$均是要计算的量。$\sigma^2$可以为已知量,也可以作为未知量一同参与计算,这里为了简化计算过程,将$\sigma^2$作为已知量处理。Probabilistic PCA相对于PCA能够更好地处理数据中的噪音,具有更高的扩展性。接下来使用最大似然估计和EM算法对该问题进行求解,EM算法的详细介绍可参考文章EM算法和高斯混合模型GMM介绍。
矩阵$W$的最大似然估计值可以写为$$W_{\mathrm{ML}}=\arg \max _{W} \ln p\left(\vec{x}_{1}, \ldots, \vec{x}_{n} | W\right)=\arg \max _{W} \sum_{i=1}^{n} \ln p\left(\vec{x}_{i} | W\right)=\arg \max_{W} \sum_{i=1}^{n} \int q\left(\vec{z}_i\right) \ln p\left(\vec{x}_{i} | W\right) d \vec{z}_{i}$$将其写成EM算法可以求解的形式:$$\begin{aligned} \sum_{i=1}^{n} \int q\left(\vec{z}_i\right) \ln p\left(\vec{x}_{i} | W\right) d \vec{z}_{i} & = \sum_{i=1}^{n} \int q\left(\vec{z}_{i}\right) \ln \frac{p\left(\vec{x}_{i}, \vec{z}_{i} | W\right)}{q\left(\vec{z}_{i}\right)} d \vec{z}_{i} \quad \leftarrow \quad \mathcal{L} \\ &+\sum_{i=1}^{n} \int q\left(\vec{z}_{i}\right) \ln \frac{q\left(\vec{z}_{i}\right)}{p\left(\vec{z}_{i} | \vec{x}_{i}, W\right)} d \vec{z}_{i} \quad \leftarrow \mathrm{KL} \end{aligned}$$
E-step:令KL=0,即令$q_t\left(\vec{z}_{i}\right)$等于$p\left(\vec{z}_{i} | \vec{x}_{i}, W_t\right)$,根据贝叶斯定理,有公式$$p\left(\vec{z}_{i} | \vec{x}_{i}, W_t\right)=\frac{p(\vec{x}_i | \vec{z}_i,W_t) \cdot p(\vec{z}_i)}{\int p(\vec{x}_i | \vec{z}_i,W_t) \cdot p(\vec{z}_i) d\vec{z}_i}=N(\vec{\mu}_i^{(t)},C_{i}^{(t)})$$其中$p(\vec{z}_i)=N(0,I),\text{ }p(\vec{x}_i | \vec{z}_i,W_t)=N\left(W_t{\vec{z}_{i}}, \sigma^{2} I\right),\text{ }C_{i}^{(t)}=\left(I+W_t^{T} W_t / \sigma^{2}\right)^{-1},\text{ }\vec{\mu}_{i}^{(t)}=C_{i}^{(t)} W_t^{T} \vec{x}_{i} / \sigma^{2}$
M-step:更新$W$使得从E-step得到的目标函数$\mathcal{L}$最大化,$\mathcal{L}$可写为如下形式:$$\mathcal{L}= \sum_{i=1}^{n} \int q_t\left(\vec{z}_{i}\right) \ln \frac{p\left(\vec{x}_{i}, \vec{z}_{i} | W\right)}{q_t\left(\vec{z}_{i}\right)} d \vec{z}_{i}=\sum_{i=1}^{n} \int q_t\left(\vec{z}_{i}\right) [\ln p(\vec{z}_i) + \ln p(\vec{x}_i | \vec{z}_i,W) - \ln q_t\left(\vec{z}_{i}\right)] d \vec{z}_{i}$$由上述公式可以得到(省略了$\mathcal{L}$中的常数项):$$W_{t+1}=\arg\max_{W}\sum_{i=1}^{n} \int q_t\left(\vec{z}_{i}\right) \ln p(\vec{x}_i | \vec{z}_i,W) d \vec{z}_{i}=\left[\sum_{i=1}^{n} \vec{x}_{i} \vec{\mu}_{i}^{(t)T}\right]\left[\sigma^{2} I+\sum_{i=1}^{n}\left(\vec{\mu}_{i}^{(t)} \vec{\mu}_{i}^{(t)T}+C_{i}^{(t)}\right)\right]^{-1}$$
Iterate E-step以及M-step直到$\sum_{i=1}^{n} \ln p\left(\vec{x}_{i} | W\right)$的增加很少为止,此时得到的$W$以及$\vec{z}_i$的后验分布$p\left(\vec{z}_{i} | \vec{x}_{i}, W\right)$即是最终的结果。
Kernel PCA
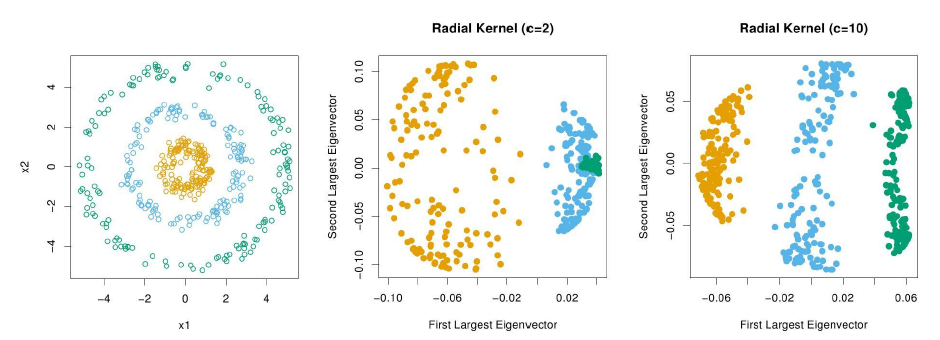
类似于Kernel SVM(参考文章支持向量机SVM介绍),Kernel PCA在PCA的基础上引入了核的思想,即先对数据集$X$进行非线性的特征变换,映射到更高维的空间中,获取关于数据的更多信息,再从高维空间上使用PCA降维,去除数据的冗余特征。由文章PCA与LDA介绍可知PCA的求解过程就是求解协方差矩阵$Q=\tilde{X}^{T} \tilde{X}$的特征值和单位特征向量。假设特征变换函数为$\vec{\phi}(\vec{x})=\left[\begin{array} {c} {\phi_1(\vec{x})} & {\phi_2(\vec{x})} & {\cdots} & {\phi_P(\vec{x})}\end{array}\right]^T$,则经过特征变换后的协方差矩阵的形式为$$Q_{K}=\sum_{i=1}^n[\vec{\phi}(\vec{x}_i)-\vec{\mu}_K][\vec{\phi}(\vec{x}_i)-\vec{\mu}_K]^T=\sum_{i=1}^n\vec{\psi}(\vec{x}_i)\vec{\psi}(\vec{x}_i)^T,\text{ where }\vec{\mu}_K=\frac{\sum_{i=1}^n\vec{\phi}(\vec{x}_i)}{n}$$矩阵$Q_K$的特征值和单位特征向量可写为$\sum_{i=1}^n\vec{\psi}(\vec{x}_i)[\vec{\psi}(\vec{x}_i)^T\vec{p}]=\lambda\vec{p}$,将$\vec{p}$的形式改写为$$\vec{p}=\sum_{i=1}^na_i\vec{\psi}(\vec{x}_i),\text{ where }a_i=\frac{\vec{\psi}(\vec{x}_i)^T\vec{p}}{\lambda}$$将该形式重新带入特征值和特征向量的公式:$$\sum_{i=1}^{n} \vec{\psi}\left(\vec{x}_{i}\right) \sum_{j=1}^{n} a_{j} \underbrace{\vec{\psi}\left(\vec{x}_{i}\right)^{T} \vec{\psi}\left(\vec{x}_{j}\right)}_{=\bar{K}_{ij}}=\lambda \sum_{j=1}^{n} a_{j} \vec{\psi}\left(\vec{x}_{j}\right)$$其中$\bar{K}$表示中心化的核矩阵。将上式两边同时左乘向量$ \vec{\psi}\left(\vec{x}_{l}\right)^T$,有$\sum_{j=1}^{n}[\sum_{i=1}^n\bar{K}_{li}\bar{K}_{ij}]a_j=\lambda\sum_{j=1}^n\bar{K}_{lj}a_j$。令$l=1,2,\cdots,n$,可以看出$\bar{K}^2\vec{a}=\lambda\bar{K}\vec{a}$,即$$\bar{K}\vec{a}=\lambda\vec{a},\text{ where }\vec{a}=\left[\begin{array} {c} a_1 & a_2 & {\cdots} & a_n\end{array}\right]^T \text{ is the eigenvector of }\bar{K}$$总结一下上述过程,即通过求解中心化的核矩阵$\bar{K}$的特征值$\lambda$和特征向量$\vec{a}$,得到经过特征变换后的协方差矩阵$Q_K$的特征值$\lambda$以及特征向量$\vec{p}=\sum_{i=1}^na_i\vec{\psi}(\vec{x}_i)$。另外由于$\vec{p}$为单位向量,$\vec{a}$需满足$\vec{p}^T\vec{p}=\sum_{i=1}^n\sum_{j=1}^na_i\vec{\psi}\left(\vec{x}_{i}\right)^{T} \vec{\psi}\left(\vec{x}_{j}\right)a_j=\vec{a}^T\bar{K}\vec{a}=\lambda\vec{a}^T\vec{a}=1$。
因此Kernel PCA的求解就转化为了两个问题的求解:求解中心化的核矩阵$\bar{K}$以及求解数据在$\vec{p}$上的投影(即坐标值):
- 假设使用高斯核函数,则核矩阵$K$中的元素$K_{ij}=\vec{\phi}\left(\vec{x}_{i}\right)^{T} \vec{\phi}\left(\vec{x}_{j}\right)=kernel(\vec{x}_i,\vec{x}_j)= \exp \left(-\frac{\left\|\vec{x}_{i}-\vec{x}_{j}\right\|^{2}}{c}\right)$,有公式$$\bar{K}_{ij}=K_{ij}-\frac{1}{n}\sum_{m=1}^nK_{mj}-\frac{1}{n}\sum_{m=1}^nK_{im}+\frac{1}{n^2}\sum_{s=1}^n\sum_{t=1}^nK_{st}$$转化为矩阵形式,可以得到$$\bar{K}=K-\frac{1}{n}IK-\frac{1}{n}KI+\frac{1}{n^2}IKI,\text{ where }I_{ij}=1,i\in\{1,2,\cdots,n\},j\in\{1,2,\cdots,n\}$$
- 数据$\vec{x}$在$\vec{p}$上的投影可以表示为$\vec{\phi}(\vec{x})^T\vec{p}=\sum_{i=1}^na_i[\vec{\phi}(\vec{x})^T\vec{\phi}(\vec{x}_i)-\frac{1}{n}\sum_{j=1}^n\vec{\phi}(\vec{x})^T\vec{\phi}(\vec{x}_j)]$。由$a_i=\frac{\vec{\psi}(\vec{x}_i)^T\vec{p}}{\lambda}$可知$\sum_{i=1}^na_i=0$,投影可表示为$\sum_{i=1}^na_i\vec{\phi}(\vec{x})^T\vec{\phi}(\vec{x}_i)$。若$\vec{x}=\vec{x}_m,\text{ }m\in\{1,2,\cdots,n\}$,则上述投影变为$\sum_{i=1}^na_iK_{mi}$;若$\vec{x}$为新的数据,则上述投影可写为$\sum_{i=1}^na_i\exp \left(-\frac{\left\|\vec{x}-\vec{x}_{i}\right\|^{2}}{c}\right)$
实际计算中通常先将数据集$X$进行标准化,再按照上述这些步骤进行计算,需要注意的是标准化后的$X$经过特征变换后的特征均值不一定仍为0,即$\frac{\sum_{i=1}^n\vec{\phi}(\vec{x}_i)}{n}\neq\vec{0}$。
t-SNE
相比于PCA等降维算法,t-SNE(t-distributed stochastic neighbor embedding)的一个主要优点是在从高维到低维的映射中尽可能保留了数据集的局地结构,即在高维空间相似的两个数据点,映射到低维空间也是相似的。
高维空间的相似性
常规的做法是用欧式距离表示这种相似性,而t-SNE使用高斯分布在高维空间中把这种距离关系转换为条件概率来表示相似性:$$p_{j | i}=\frac{\exp \left(-\left\|\vec{x}_{j}-\vec{x}_{i}\right\|^{2} / 2 \sigma_{i}^{2}\right)}{\sum_{k \neq i} \exp \left(-\left\|\vec{x}_{k}-\vec{x}_{i}\right\|^{2} / 2 \sigma_{i}^{2}\right)}$$针对方差$\sigma_{i}^{2}$的确定,首先提前给定perpexility的值,由信息论可知:$$perpexility=2^{H_i}=2^{-\sum_{j \neq i}p_{j | i}\log_2 p_{j | i}},\text{ where }H_i \text{ is the entropy of distribution } p(\cdot | i)$$通过上述公式求得对应的$\sigma_{i}^{2}$,给定的perpexility越小,求得的方差也越小。在t-SNE中可以将perpexility等价地看作每个点的邻近点个数,一般来说比较合理的取值区间为[5, 50]。此外,使用$p(i | j)$的一个问题是它不是对称的,即$p_{i | j} \neq p_{j | i}$,为了能得到一个更加通用的联合概率分布,使得$p_{ij}=p_{ji}$,定义$p_{i j}=\frac{p_{j | i}+p_{i | j}}{2 n},\text{ }p_{ii}=0$。
高维向低维的映射
为了解决高维数据集映射到低维后产生的拥挤问题(The Crowding Problem),在低维空间中选择长尾的$t$分布(通常令自由度为1,即柯西分布)来度量相似性:$$q_{i j}=\frac{\left(1+\left\|\vec{y}_{i}-\vec{y}_{j}\right\|^{2}\right)^{-1}}{\sum_{k \neq l}\left(1+\left\|\vec{y}_{k}-\vec{y}_{l}\right\|^{2}\right)^{-1}}$$利用KL散度来衡量高维和低维两个分布的相似性,即$$C=K L(P \| Q)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}}$$为了求得低维空间中的$\vec{y}_i,\text{ }i=1,2,\cdots,n$,采用梯度下降法求解$C$的最小值,梯度公式如下:$$\frac{\partial C}{\partial \vec{y}_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(\vec{y}_{i}-\vec{y}_{j}\right)\left(1+\left\|\vec{y}_{i}-\vec{y}_{j}\right\|^{2}\right)^{-1}$$值得注意的一点是最终在低维空间上求得的数据集,它的不同集群之间的距离并没有实际意义,因为对$t$分布来说,超出一定距离范围以后,其相似度都是很小的;另外t-SNE不适合用来寻找离群点,因为使用对称的$p_{ij}$相当于无形之中拉近了集群和离群点之间的距离。下图表示在MNIST数据集上使用t-SNE进行可视化的结果:

参考资料
针对t-SNE更详细的介绍和应用可以参考以下文章



