回归问题示例
所用数据可从这里下载(提取码1fl1),数据说明可参考此文件(提取码7tvm),目标是分析建筑物的节能之星评分(ENERGY STAR Score)与哪些因素有关,并对之进行预测。
一个完整的机器学习项目主要有以下几个步骤组成:
- 探索性数据分析(EDA)
- 特征工程和选择(Feature Engineering and Selection)
- 机器学习模型比较(Model Comparison)
- 超参数调优(Hyperparameters Tuning)
- 模型评估和解释(Model Evaluation and Interpretation)
1. 探索性数据分析
- Read data and Confirm data type
 View Code
View Codeimport pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from IPython.core.pylabtools import figsize from sklearn.model_selection import train_test_split from sklearn.preprocessing import Imputer, FunctionTransformer, MinMaxScaler, LabelBinarizer from sklearn_pandas import DataFrameMapper, CategoricalImputer from sklearn.pipeline import Pipeline data = pd.read_csv('Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016.csv') data = data.replace({'Not Available': np.nan}) numeric_units = ['ft²','kBtu','Metric Tons CO2e','kWh','therms','gal','Score'] for col in list(data.columns): for unit in numeric_units: # Select columns that should be numeric if unit in col: # Convert the data type to float data[col] = data[col].astype(float)
- Check missing value
 View Code
View Codedef missing_values_table(df): # Total missing values mis_val = df.isnull().sum() # Percentage of missing values mis_val_percent = 100 * df.isnull().sum() / len(df) # Make a table with the results mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1) # Rename the columns mis_val_table = mis_val_table.rename(columns = {0 : 'Missing Values', 1 : '% of Total Values'}) # Sort the table by percentage of missing descending mis_val_table = mis_val_table[mis_val_table.iloc[:,1] != 0].sort_values('% of Total Values', ascending=False).round(1) # Return the dataframe with missing information return mis_val_table missing_df = missing_values_table(data) ### drop the columns that have >50% missing values missing_columns = list(missing_df[missing_df['% of Total Values'] > 50].index) print('We will remove %d columns.' % len(missing_columns)) data = data.drop(columns = missing_columns)
- Remove Outliers
 View Code
View Code# Calculate first and third quartile first_quartile = data['Site EUI (kBtu/ft²)'].describe()['25%'] third_quartile = data['Site EUI (kBtu/ft²)'].describe()['75%'] iqr = third_quartile - first_quartile #Interquartile range data = data[(data['Site EUI (kBtu/ft²)'] > (first_quartile - 3 * iqr)) & \ (data['Site EUI (kBtu/ft²)'] < (third_quartile + 3 * iqr))]
- Histogram of the target
 View Code
View Code### Histogram of the Energy Star Score(the target) data = data.rename(columns = {'ENERGY STAR Score': 'score'}) plt.style.use('fivethirtyeight') plt.hist(data['score'].dropna(), bins = 100, edgecolor = 'k') plt.xlabel('Score'); plt.ylabel('Number of Buildings') plt.title('Energy Star Score Distribution')
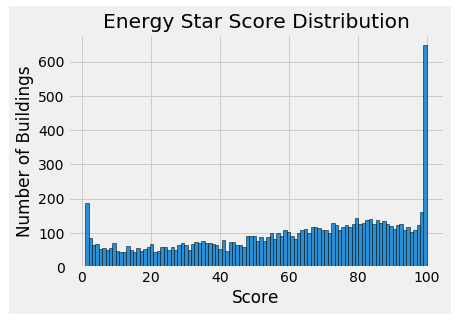
- Correlations between the target and numerical variables
 View Code
View Code# Find all correlations and sort correlations_data = data.corr()['score'].sort_values() # Print the most negative correlations print(correlations_data.head(15), '\n') # Print the most positive correlations print(correlations_data.tail(15))
- Plot distributions of the target for a categorical variable
 View Code
View Code# Create a list of building types with more than 100 observations types = data.dropna(subset=['score']) types = types['Largest Property Use Type'].value_counts() types = list(types[types.values > 100].index) # Plot each building sns.set(font_scale = 1) figsize(6, 5) for b_type in types: # Select the building type subset = data[data['Largest Property Use Type'] == b_type] # Density plot of Energy Star scores sns.kdeplot(subset['score'].dropna(), label = b_type, shade = False, alpha = 0.8) # label the plot plt.xlabel('Energy Star Score', size = 10) plt.ylabel('Density', size = 10) plt.title('Density Plot of Energy Star Scores by Building Type', size = 14)

- Visualization of the target vs a numerical variable and a categorical variable
 View Code
View Codetemp = data.dropna(subset=['score']) # Limit to building types with more than 100 observations temp = temp[temp['Largest Property Use Type'].isin(types)] # Visualization figsize(9, 7.5) sns.set(font_scale = 2) sns.lmplot('Site EUI (kBtu/ft²)', 'score', hue = 'Largest Property Use Type', data = temp, \ scatter_kws = {'alpha': 0.8, 's': 60}, fit_reg = False, size = 12, aspect = 1.2) # Plot labeling plt.xlabel("Site EUI", size = 28) plt.ylabel('Energy Star Score', size = 28) plt.title('Energy Star Score vs Site EUI', size = 36)

- Pair Plot
 View Code
View Code# Extract the columns to plot plot_data = data[['score', 'Site EUI (kBtu/ft²)', 'Weather Normalized Source EUI (kBtu/ft²)']] # Replace the inf with nan plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan}) # Rename columns plot_data = plot_data.rename(columns = {'Site EUI (kBtu/ft²)': 'Site EUI', \ 'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI'}) # Drop na values plot_data = plot_data.dropna() # Function to calculate correlation coefficient between two columns def corr_func(x, y, **kwargs): r = np.corrcoef(x, y)[0][1] ax = plt.gca() ax.annotate("r = {:.2f}".format(r), xy=(.2, .8), xycoords=ax.transAxes, size = 20) # Create the pairgrid object figsize(9,7.5) sns.set(font_scale = 1) grid = sns.PairGrid(data = plot_data, height = 3) # Upper is a scatter plot grid.map_upper(plt.scatter, color = 'red', alpha = 0.6) # Diagonal is a histogram grid.map_diag(plt.hist, color = 'red', edgecolor = 'black') # Bottom is correlation and density plot grid.map_lower(corr_func); grid.map_lower(sns.kdeplot, cmap = plt.cm.Reds) # Title for entire plot plt.suptitle('Pairs Plot of Energy Data', size = 24, y = 1.02)
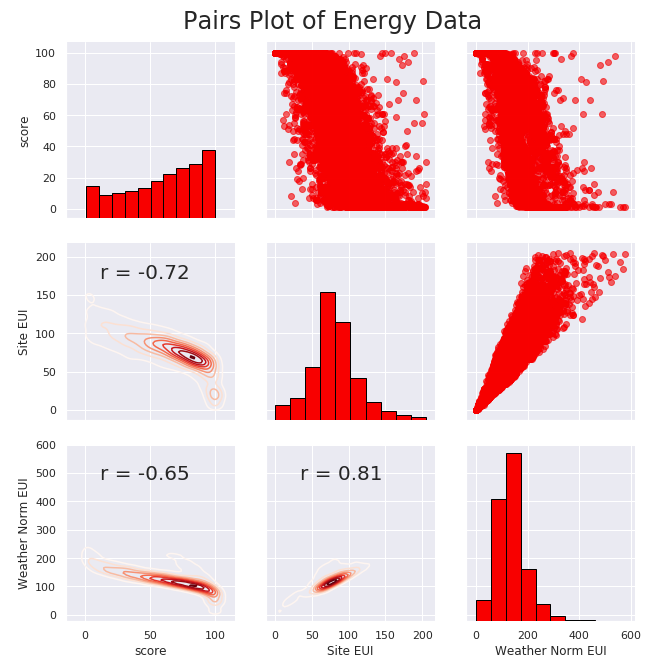
2. 特征工程和选择
- 特征工程
 View Code
View Code### Extract the buildings with no score and the buildings with a score numeric_cols = data.columns[data.dtypes!=object].tolist() categorical_cols = ['Borough', 'Largest Property Use Type'] no_score = data[numeric_cols+categorical_cols][data['score'].isna()] #for prediction score = data[numeric_cols+categorical_cols][data['score'].notnull()] ### Separate out the features and targets features = score.drop(columns='score') targets = pd.DataFrame(score['score']) numeric_cols.remove('score') ### Split into 70% training and 30% testing set X, X_test, y, y_test = train_test_split(features, targets, test_size = 0.3, random_state = 42) ### Create columns with log of numeric columns def add_log(df): temp = df.copy() for col in numeric_cols: temp['log_' + col] = np.sign(df[col])*np.log(np.abs(df[col])+1) return temp ### Apply numeric imputer and min-max transform cols = numeric_cols+['log_'+col for col in numeric_cols] numeric_imputer = [([feature], [Imputer(strategy="median"),MinMaxScaler(feature_range=(0, 1))]) \ for feature in cols] ### Apply categorical imputer and one-hot encode category_imputer = [(feature, [CategoricalImputer(strategy='constant', fill_value='Missing'),LabelBinarizer()]) \ for feature in categorical_cols] ### union mapper mapper = DataFrameMapper(numeric_imputer+category_imputer, input_df=True, df_out=True) ### feature engineer pipeline fea_engine = Pipeline([("add_log", FunctionTransformer(add_log, validate=False)), \ ("num_cat_mapper", mapper)]) X_engine = fea_engine.fit_transform(X) X_test_engine = fea_engine.transform(X_test)
- 特征选择
 View Code
View Code### Remove collinear features in a dataframe with a correlation coefficient greater than the threshold. ### Removing collinear features can help a model to generalize and improves the interpretability of the model. ### pakage feature_selector: https://github.com/WillKoehrsen/feature-selector from feature_selector import FeatureSelector cols = numeric_cols+['log_'+col for col in numeric_cols] fs = FeatureSelector(data = X_engine[cols], labels = y) fs.identify_collinear(correlation_threshold=0.8) correlated_features = fs.ops['collinear'] print(fs.record_collinear) #打印相关系数的详细信息 X_select = X_engine.drop(columns = correlated_features) X_test_select = X_test_engine.drop(columns = correlated_features) ### Write to files for next modeling no_score.to_csv('data/no_score.csv', index = False) X_select.to_csv('data/training_features.csv', index = False) X_test_select.to_csv('data/testing_features.csv', index = False) y.to_csv('data/training_labels.csv', index = False) y_test.to_csv('data/testing_labels.csv', index = False)
3. 机器学习模型比较

from sklearn.linear_model import LinearRegression from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor from sklearn.svm import SVR from sklearn.neighbors import KNeighborsRegressor ### Read data train_features = pd.read_csv('data/training_features.csv') test_features = pd.read_csv('data/testing_features.csv') train_labels = pd.read_csv('data/training_labels.csv') test_labels = pd.read_csv('data/testing_labels.csv') ### Function to calculate mean absolute error def mae(y_true, y_pred): return np.mean(abs(y_true - y_pred)) ### Create a baseline baseline_guess = np.median(train_labels) print('The baseline guess is a score of %0.2f' % baseline_guess) print("Baseline Performance on the test set: MAE = %0.4f" % mae(test_labels, baseline_guess)) ### Model Comparison def fit_and_evaluate(model): model.fit(train_features, train_labels.values.reshape((-1,))) #train the model model_pred = model.predict(test_features) #predict the model model_mae = mae(test_labels.values.reshape((-1,)), model_pred) #compute the metric return model_mae lr = LinearRegression() #Linear Regression lr_mae = fit_and_evaluate(lr) print('Linear Regression Performance on the test set: MAE = %0.4f' % lr_mae) svm = SVR(C = 1000, gamma = 0.1) svm_mae = fit_and_evaluate(svm) #SVR print('Support Vector Machine Regression Performance on the test set: MAE = %0.4f' % svm_mae) random_forest = RandomForestRegressor(random_state=60) #Random Forest random_forest_mae = fit_and_evaluate(random_forest) print('Random Forest Regression Performance on the test set: MAE = %0.4f' % random_forest_mae) gradient_boosted = GradientBoostingRegressor(random_state=60) #GBM gradient_boosted_mae = fit_and_evaluate(gradient_boosted) print('Gradient Boosted Regression Performance on the test set: MAE = %0.4f' % gradient_boosted_mae) knn = KNeighborsRegressor(n_neighbors=10) #KNN knn_mae = fit_and_evaluate(knn) print('K-Nearest Neighbors Regression Performance on the test set: MAE = %0.4f' % knn_mae) ### Visualization plt.style.use('fivethirtyeight') figsize(8, 6) model_comparison = pd.DataFrame({'model': ['Linear Regression', 'SVR', 'RF', 'GBM', 'KNN'], \ 'mae': [lr_mae, svm_mae, random_forest_mae, gradient_boosted_mae, knn_mae]}) # Dataframe to hold the results model_comparison.sort_values('mae', ascending = False).plot(x = 'model', y = 'mae', \ kind = 'barh', color = 'red', edgecolor = 'black') # Horizontal bar chart of test mae plt.ylabel(''); plt.yticks(size = 14); plt.xlabel('Mean Absolute Error'); plt.xticks(size = 14) plt.title('Model Comparison on Test MAE', size = 20)

4. 超参数调优

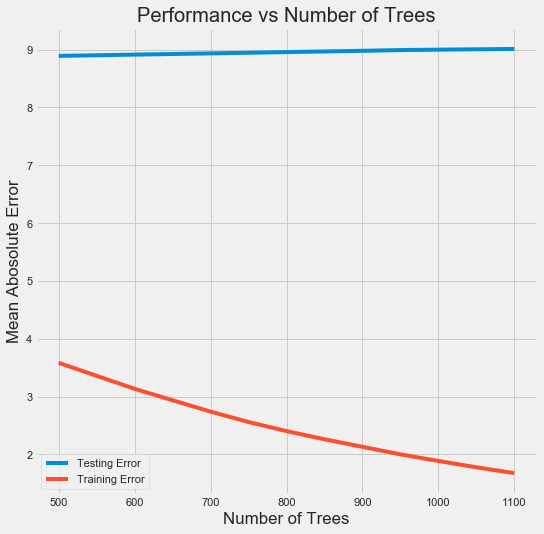
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV ### Create the model to use for hyperparameter tuning model = GradientBoostingRegressor(random_state=60) ### Set tuned hyperparameters loss = ['ls', 'lad', 'huber'] n_estimators = [100, 500, 900, 1100, 1500] max_depth = [2, 3, 5, 10, 15] min_samples_leaf = [1, 2, 4, 6, 8] min_samples_split = [2, 4, 6, 10] max_features = ['sqrt', 'log2', None] hyperparameter_grid = {'loss': loss, 'n_estimators': n_estimators, 'max_depth': max_depth, \ 'min_samples_leaf': min_samples_leaf, 'min_samples_split': min_samples_split, \ 'max_features': max_features} ### Set up the random search with 4-fold cross validation random_cv = RandomizedSearchCV(estimator=model, param_distributions=hyperparameter_grid, \ cv=4, n_iter=25, scoring='neg_mean_absolute_error', n_jobs=-1, \ verbose=1, random_state=60) random_cv.fit(train_features, train_labels.values.reshape((-1,))) print(random_cv.best_estimator_) ### Further grid search for the model model = random_cv.best_estimator_ trees_grid = {'n_estimators': [500, 600, 700, 750, 800, 850, 900, 950, 1000, 1050, 1100]} grid_search = GridSearchCV(estimator=model, param_grid=trees_grid, cv=4, verbose=1, \ scoring='neg_mean_absolute_error', n_jobs=-1) grid_search.fit(train_features, train_labels.values.reshape((-1,))) ### Plot the training and testing error vs number of trees results = pd.DataFrame(grid_search.cv_results_) figsize(8, 8) plt.style.use('fivethirtyeight') plt.plot(results['param_n_estimators'], -1 * results['mean_test_score'], label = 'Testing Error') plt.plot(results['param_n_estimators'], -1 * results['mean_train_score'], label = 'Training Error') plt.xlabel('Number of Trees'); plt.ylabel('Mean Abosolute Error'); plt.legend() plt.title('Performance vs Number of Trees') #下图 ### 由下图可以看出过拟合现象,因此再进行一轮grid search,希望能够改善过拟合 of_grid = {'n_estimators': [100,200,300,400,500], 'min_samples_leaf': [1,2], 'min_samples_split': [2,4], 'max_depth': [3,5]} grid_search_of = GridSearchCV(estimator=grid_search.best_estimator_, param_grid=of_grid, cv=4, verbose=1, \ scoring='neg_mean_absolute_error', n_jobs=-1) grid_search_of.fit(train_features, train_labels.values.reshape((-1,))) ### Final Model final_model = grid_search_of.best_estimator_ print(final_model) final_mae = fit_and_evaluate(final_model) print('Final model performance on the test set: MAE = %0.4f.' % final_mae) #MAE: 9.02
5. 模型评估和解释
- 预测缺失的评分
 View Code
View Codeno_score = pd.read_csv('data/no_score.csv').drop(columns='score') no_score_engine = fea_engine.transform(no_score) no_score_select = no_score_engine.drop(columns = correlated_features) final_model = grid_search_of.best_estimator_ final_model.fit(train_features, train_labels.values.reshape((-1,))) score_preds = final_model.predict(no_score_select) score_preds = np.where(score_preds>100, 100, score_preds) score_preds = np.where(score_preds<0, 0, score_preds) ### Plot plt.style.use('fivethirtyeight') plt.hist(score_preds, bins = 100, edgecolor = 'k') plt.xlabel('Predicted Score'); plt.ylabel('Number of Buildings') plt.title('Energy Star Score Distribution')

- 特征重要性
 View Code
View Code# Extract the feature importances into a dataframe feature_results = pd.DataFrame({'feature': list(train_features.columns), 'importance': final_model.feature_importances_}) # Show the top 10 most important feature_results = feature_results.sort_values('importance', ascending = False).reset_index(drop=True) print(feature_results.head(10))
- Locally Interpretable Model-agnostic Explanations(LIME)
 View Code
View Codeimport lime import lime.lime_tabular ### Find the residuals residuals = abs(final_model.predict(test_features) - test_labels.values.reshape((-1,))) ### Extract the worst prediction wrong = test_features.values[np.argmax(residuals), :] ### Create a lime explainer object explainer = lime.lime_tabular.LimeTabularExplainer(training_data = train_features.values, \ categorical_features=list(range(25,len(train_features.columns))), \ mode = 'regression', \ training_labels = train_labels.values.reshape((-1,)), \ feature_names = list(train_features.columns)) ### Explanation for wrong prediction print('Prediction: %0.4f' % final_model.predict(wrong.reshape(1, -1))) print('Actual Value: %0.4f' % test_labels.values.reshape((-1,))[np.argmax(residuals)]) wrong_exp = explainer.explain_instance(data_row = wrong, predict_fn = final_model.predict) ### Plot the prediction explaination wrong_exp.as_pyplot_figure() plt.title('Explanation of Prediction for the Wrong Case', size = 28) plt.xlabel('Effect on Prediction', size = 22)
关于LIME的介绍可参考这篇文章,上述代码仅分析了模型预测最不准确的那个例子。从下图可以看出在该例中模型预测值偏低的主要原因是Site EUI以及Weather Normalized Site Electricity Intensity的值较高;这两个值越高,建筑物的节能之星评分就越低,这是模型经过训练所总结出来的性质。在该例中虽然这两个值很高,但是建筑物的实际节能之星评分也很高,这就与模型经过大量数据训练所得到的经验相悖,最终造成了较大的预测误差。





