DS博客作业03--树
0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
串的BF\KMP算法
串的模式匹配中,存在一个主串和一个子串,我们需要在主串中找到子串,而寻找子串的方法有BF,以及KMP两种
BF算法:古典的,经典的算法,通过穷举来找到我们需要的子串,我们也可以称之为暴力法
基本思路:从目录串第一个字符开始和模式串第一个字符开始比较
1.相等,继续向后匹配
2.不相等,从目标串下一个字符开始比较
依据这个思路一直匹配下去,直到找到模式串,或找完目录串但是找不到模式串
如图: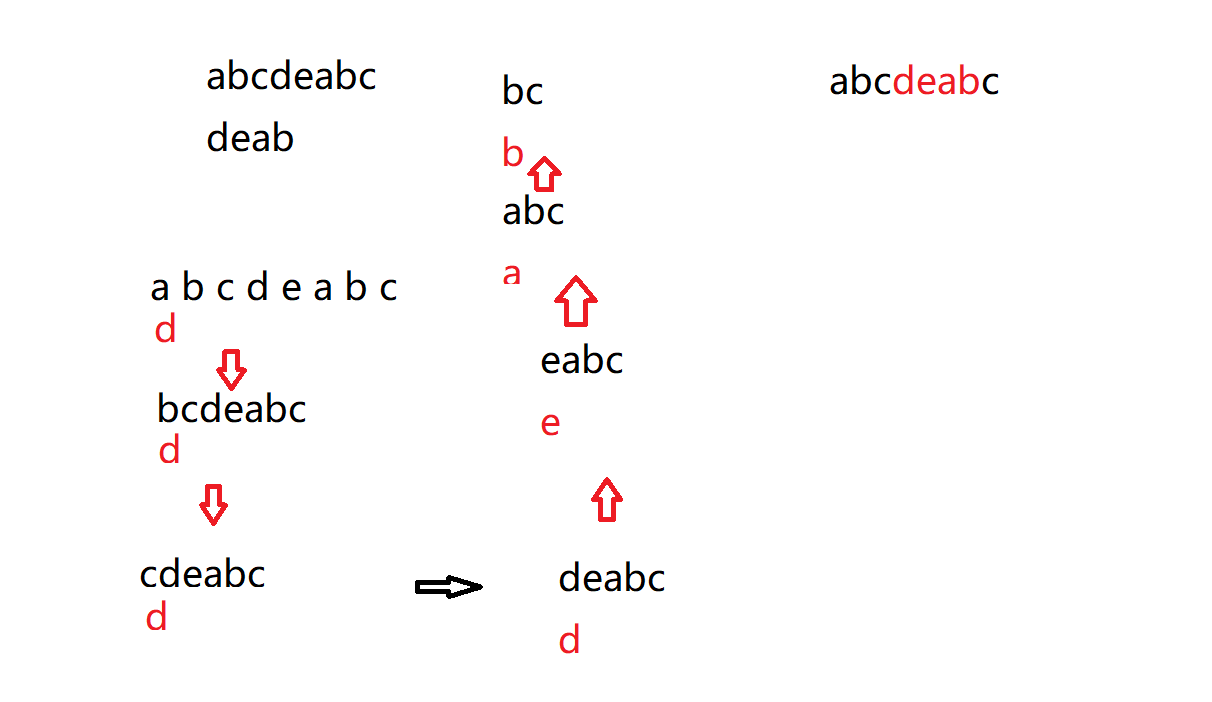
BF算法代码
int index(SqString s,SqString t)
{
int i=0,j=0;
while(i<s.length&&j<t.length)
{
if(i<s.data[i]==t.data[j])
{
i++;
j++;
}
else
{
i=i-j+1;
j=0;
}
}
if(j>=t.length)
return (i-t.length);
else
return -1;
BF算法的缺点:如果一直找不到模式串,那么我们就要一直遍历到目标串最后,或者,目标串一直符合模式串最后一个字符前所有字符,并且目标串一直如此,这样的话我们的时间复杂度会特别高,程序跑起来特别慢,由此BF算法并不是万能的,为了解决这个问题,我们引入KMP算法
KMP算法:相较于BF算法
1.主串不需要回溯
2.将模式串向右前进尽可能远
next数组:如图

通过对比模式串用next数组值保存部分匹配信息,同时如果失配时不用回到串首,直接通过next数组值就可以达到修改的目的即:
MAX{k|0<k<j,且"t0t1t2...tk-1"="tj-ktj-k+1...tj-1"} ,当此集合非空
next[j]=-1 当j=0
0 不含真子串
void GetNext(SqString t, int next[])
{
int j,k;
j=0;k=-1;next[0]=1;
while(j<t.length-1)
{
if(k==1||t.data[j]==t.data[k])
{
j++;k++:
next[j]=k;
}
else
k=next[k];
}
}
此时的KMP算法
int KMPIndex(SqString s,SqString t)
{
int next[MAXSIZE],i=0,j=0;
GetNext(t,next);
while(i<s.length&&j<t.length)
{
if(j==-1||s.data[i]==t.data[j])
{
i++;
j++;
}
else j=next[j];
}
if(j>=t.length)
return (i-t.length);
else
return -1;
}
但是next数组还存在着缺陷,所以引入了nextval数组
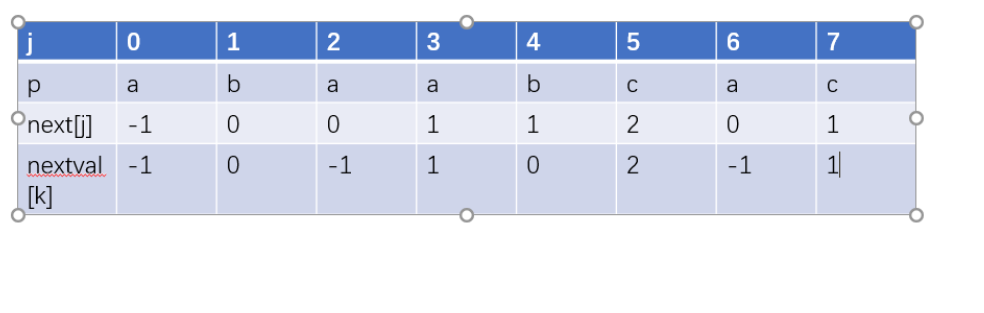
将next数组修正为nextval即
1.不等,则
nextval[j]=next[j];
2.相等
nextval[j]=nextval[k];
nextval算法代码
void GetNext(SqString t, int nextval[])
{
int j=0,k=-1;
nextval[0]=-1;
while(j<t.length)
{
if(k==-1||t.data[j]==t.data[k])
{
j++;k++;
if(t.data[j]!=t.data[k])
nextval[j]=k;
else
nextval[j]=nextval[k];
}
else
k=nextval[k];
}
}
此时修改后的KMP算法
int KMPIndexl(SqString s,SqString t)
{
int nextval[MAXSIZE],i=0,j=0;
GetNextval(t,nextval);
while(i<s.length&&j<t.length)
{
if(j==-1||s.data[i]==t.data[j])
{
i++;
j++;
}
else j=nextval[j];
}
if(j>=t.length)
return (i-t.length);
else
return -1;
}
}
二叉树存储结构、建法、遍历及应用
二叉树:是n个结点的有限集合,它可能是空树,或一个根节点和至多两棵树(左子树,右子树)的互不相交的二叉树组成,二叉树中不可能存在度大于2的结点
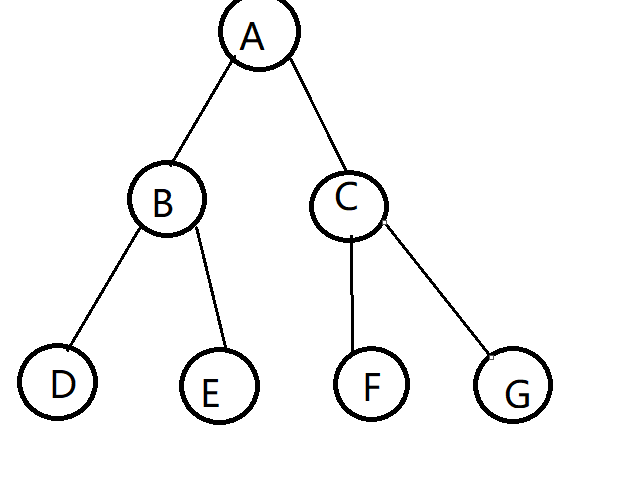
二叉树的存储结构:
1.顺序存储结构
主要方法是,对结点编号,数组存储
如:定义一个数组t
则:t[1]=A,t[2]=B...
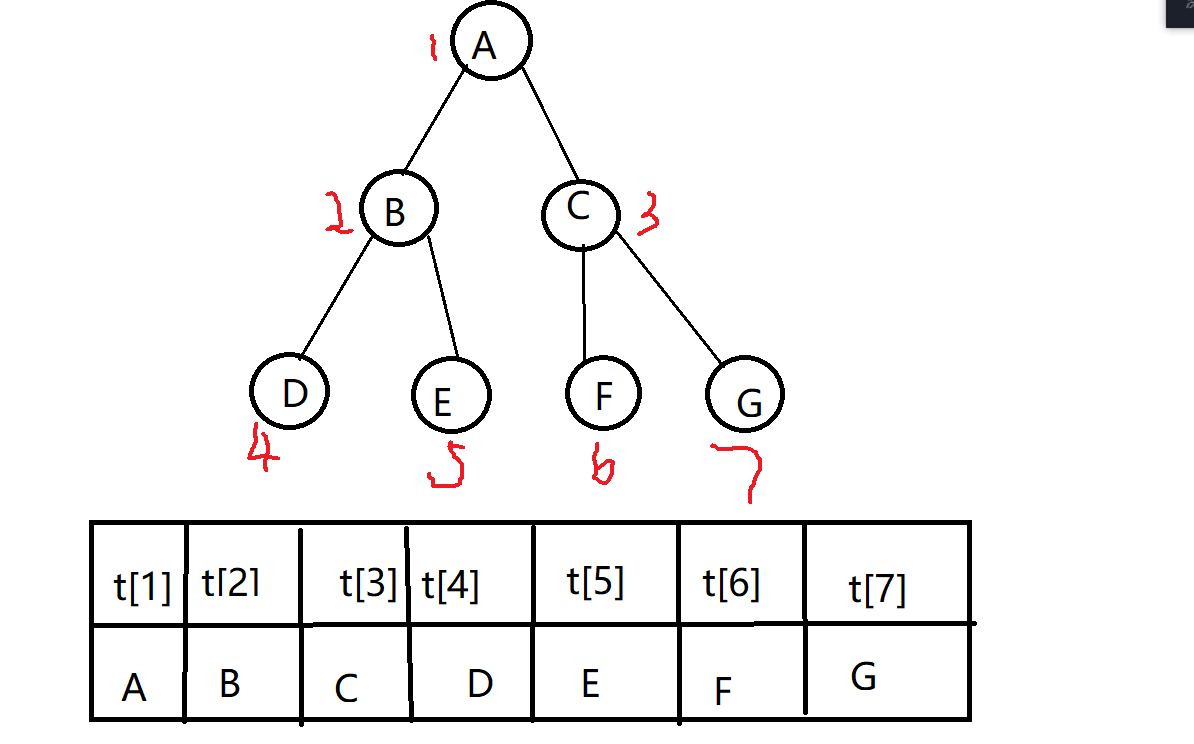
值得注意的是,用顺序存储时我们建树并不一定是完全二叉树,所以我们需要先将一般的二叉树补全,利用空格补全二叉树后再对结点进行编号
顺序存储缺点:
1.如果是完全二叉树顺序存储非常实用,但是是完全二叉树的情况特别少见,所以我们建树前都要进行补树
2.非完全二叉树建树时,补树需要占用数组空间,而原来的树所需要的数组大小需要扩大,浪费空间
3.查找,插入,删除不方便
链式存储:
对于非完全二叉树,在通过链存储时,n个结点,存在2n个指针域,n+1个空指针,n-1个非空指针
二叉树的建法:
顺序存储需要先将二叉树补满后转二叉链
先序递归建树
通过扫描字符串,用递归进行左子树创建和右子树创建
代码展示
BinTree CreatBinTree()
{
BinTree bt;
bt = new TNode;
char str;
cin >> str;
if (str == '#')
bt=NULL;
else
{
bt = new TNode;
bt->Data = str;
bt->Left= CreatBinTree();
bt->Right=CreatBinTree();
}
return bt;
}
层次法建树
代码展示
void CreateBTree(BTree &BT,string str)
{
BTree T;
int i=0;
queue<BTree>Q;
if(str[0]!='0')
{
BT=new BTNode;
BT->data=str[0];
BT->left=BT->right=NULL;
Q.push(BT);
}
else
BT=NULL;
while(!Q>empty())
{
T=Q.front();
Q.pop();
i++;
if(str[i]=='0')T->left=NULL;
else
{
T->left=new BTNode;
T->left->data=str[i];
T->left->left=T->left->right=NULL;
Q.push(T->left);
}
i++;
if(str[i]=='0')T->right=NULL;
else
{
T->right=new BTNode;
T->right->data=str[i];
T->right->left=T->right->right=NULL;
Q.push(T->right);
}
}
}
括号法字符串构造二叉树
将字符串通过多个括号与逗号分开,从而达到关系配对,之后通过左右括号配对建树
代码展示
void CreateBTNode(BTNode * &b,char *str)
{
BTNode *St[Maxsize],*p;
int top=1,k,j=0;
char ch;
b=NULL;
ch=str[j];
while(ch!='\0')
{
switch(ch)
{
case '(':top++;St[top]=-;k=1;break;
case ')':top--;break;
case',':k=2;break;
default:
p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch;
p->left=p->right=NULL;
if(b==NULL)
b=p;
else
{
switch(k)
{
case 1:St[top]->left=p;break;
case 2:St[top]->right=p;break;
}
}
}
j++;
ch=str[j];
}
}
二叉树的遍历
对同一个二叉树,不同的遍历方法输出的字符串不相同
如
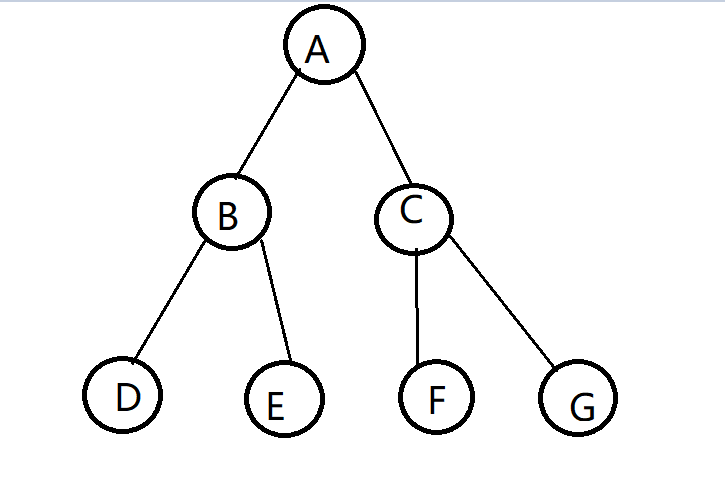
1.先序遍历:
根节点-左子树-右子树
输出为:ABDECFG
代码
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
printf(" %c", BT->Data);
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
}
2.中序遍历
左子树-根节点-右子树
输出:BDEACFG
代码
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
PreorderPrintLeaves(BT->Left);
printf(" %c", BT->Data);
PreorderPrintLeaves(BT->Right);
}
}
3.后序遍历
左子树-右子树-根节点
输出:DBEFCGA
代码
void PreorderPrintLeaves(BinTree BT)
{
if (BT != NULL)
{
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
printf(" %c", BT->Data);
}
}
层次遍历:层次遍历的输出与输入相同,应用队列的先进先出特性实现顺序输出
输出:ABCDEFG
代码
void PreorderPrintLeaves(BinTree BT)
{
int flag = 0;
queue<BinTree>tree;
if (BT != NULL)
tree.push(BT);
else
{
printf("NULL");
}
while (!tree.empty())
{
BT= tree.front();
if (flag == 0)
{
cout << BT->Data;
flag = 1;
}
else
cout << " " << BT->Data;
tree.pop();
if (BT->Left != NULL)
tree.push(BT->Left);
if (BT->Right != NULL)
tree.push(BT->Right);
}
}
二叉树的应用:表达式树
将中缀表达式转换为二叉表达式树
思路:
1.树中叶子结点均为操作数,分支结点为运算符
2.运算符栈
3.存放树根栈
表达式树中,我们需要运用到建树,排序,对比,输出,将二叉树的应用都融合到一起
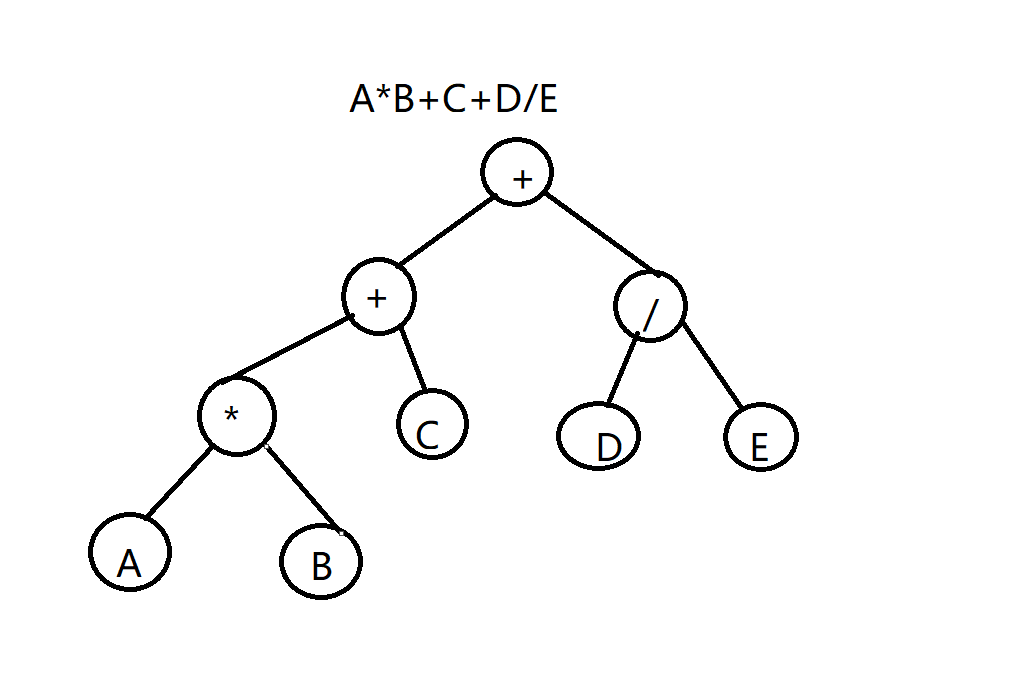
如图:根据优先性,A*B,D/E首先进行,所以二者不受其他打扰,运算后再进行下一步
树的结构、操作、遍历及应用
树:相较于二叉树这种特殊的树,我们更常见的树这种结构,而对于树来说,它的存储结构相较于二叉树就复杂许多
1.双亲存储结构
树中任何结点都有且只有唯一的双亲结点,所以我们引入一个值来记录对应结点的双亲结点
结构体定义
typedef struct
{
ElemType data;
int parent;
}PTree[Maxsize]
然而,此时我们找双亲容易,找孩子不容易,所以引入下一个存储结构
2.孩子链存储结构
我们将一个结点定义一些空指针域,而这些空指针指向的是它的孩子,这就是孩子链存储结构
结构体定义
typedef struct node
{
ElemType data;
struct node*sons[MaxSons];
}TSonNode;
但是孩子链存储结构也存在问题,那就是空指针太多了,并且找父亲不容易,于是我们引入了第三个存储结构
3.孩子兄弟链存储结构
孩子兄弟链存储结构是为每个结点设计3个域:
一个数据元素域
第一个孩子结点指针域
一个兄弟结点指针域
结构体定义
typedef struct tnode
{
ElemType data;
struct tnode* son;
struct tnode *brother;
}TSBNode;
每个结点固定只有两个指针域,类似二叉树,找父亲不容易
如果在一棵树中最常用的操作时查找某个结点的祖先结点,采用双亲存储结构合适
如果最常用的操作是查找某个结点的所有兄弟,则采用孩子存储结构或孩子兄弟链结构
树的遍历:树的遍历运算时指按某种方式访问树中的每一个结点且每一个结点只被访问一次
遍历方法:
如图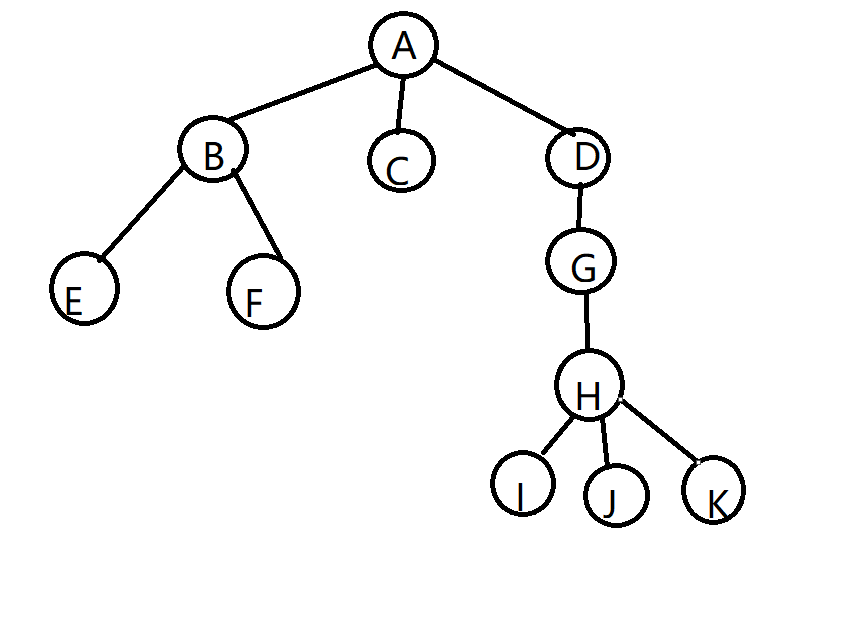
1.先根遍历:ABEFCDGHIJK
2.后根遍历:EFBCIJKHGDA
3.层次遍历:ABCDEFGHIJK
树的应用:目录树
PTA中有一道题,目录树,这题就是典型的树,同时还需要使用孩子兄弟链结构,通过关系对比建立一个个兄弟结点
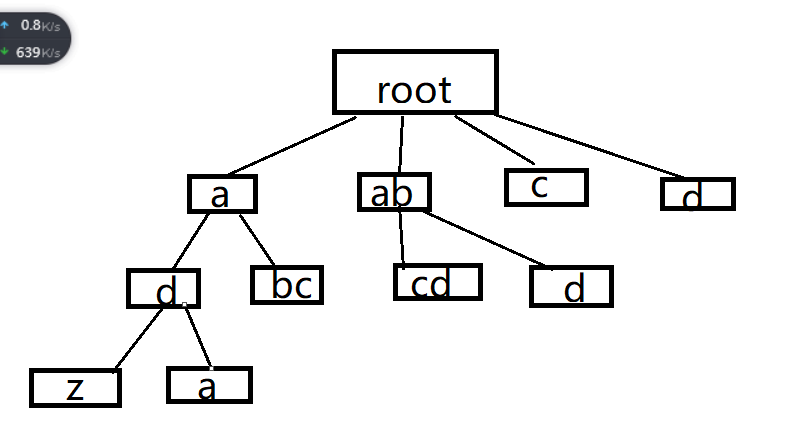
如图,每一个结点下面都有结点,同时每一个孩子结点存在兄弟结点,而兄弟结点之间也有顺序之分,孩子结点与兄弟结点,就需要应用孩子兄弟链
线索二叉树
二叉树存储结构时,每个结点有两个指针域,总共有2n个指针域,其中
有效指针域:n-1
空指针域:n+1
利用这些空链域,指向该线性序列中前驱和后继的指针,称为线索
1.若结点有左子树,则ichild指向其左孩子,否则,指向其直接前驱(即线索)
2.若结点有右子树,则rchild指向其右孩子,否则,rchild指向其直接后继(即线索)
即如图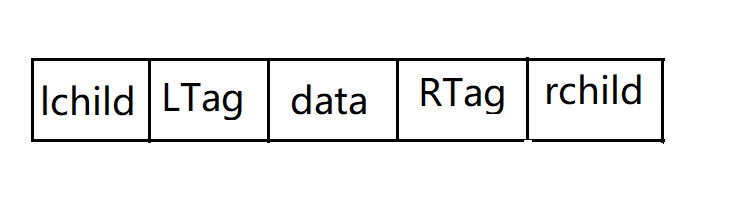
先序线索二叉树
先序序列:ABCDE
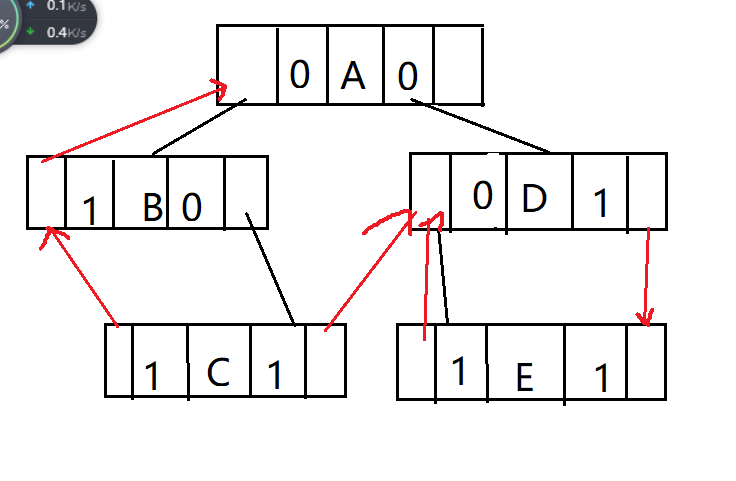
后序线索二叉树
后序序列:CBEDA
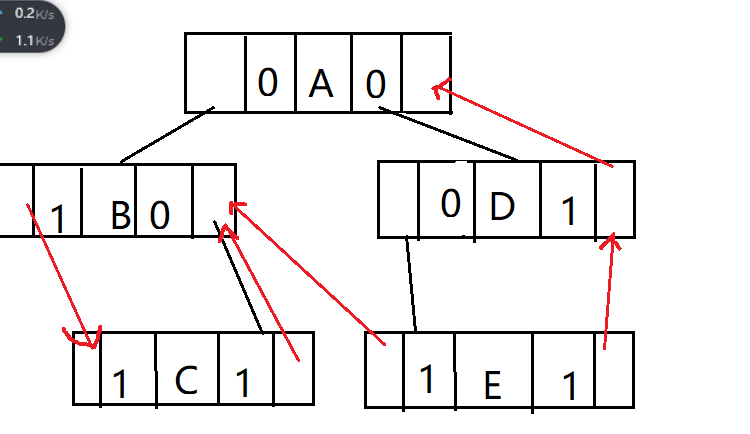
中序线索二叉树
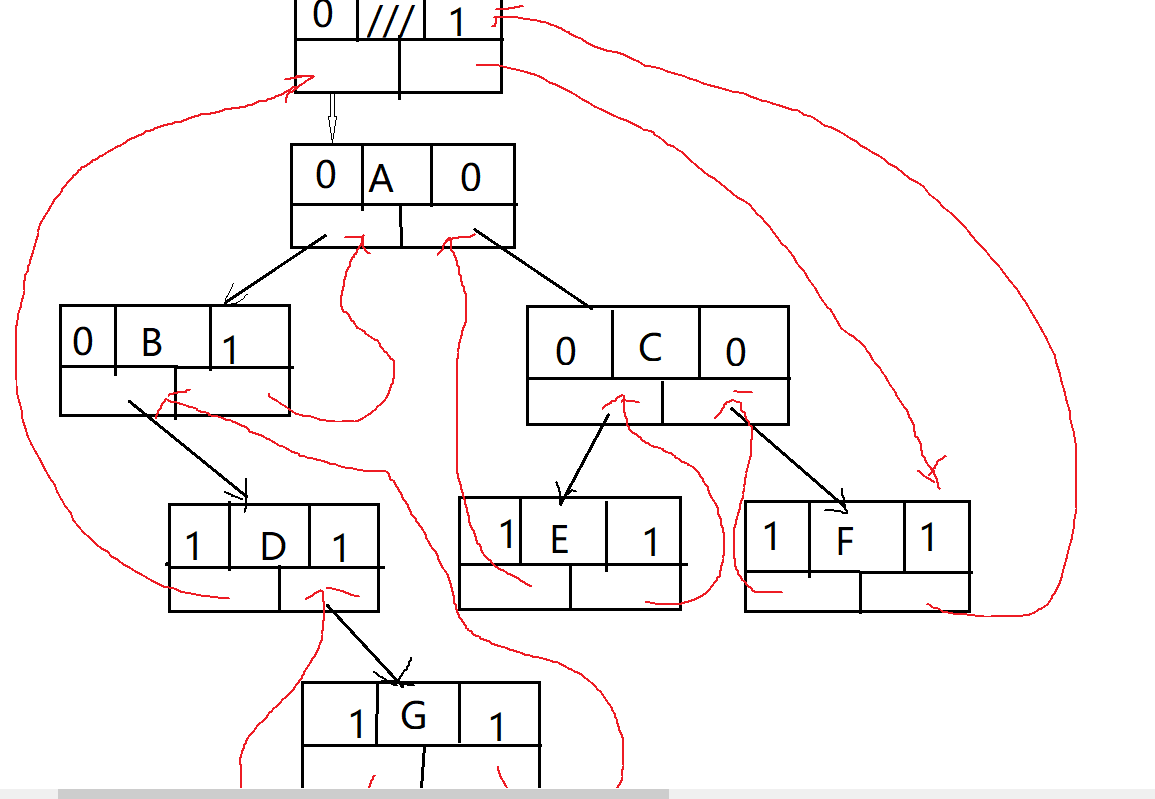
遍历线索化二叉树
1.找中序遍历的第一个结点
2.找中序线索化链表中结点的后继
代码展示
void ThInOrder(TBTNode *tb)
{
TBTNode *p=tb->lchild;
while(p!=tb)
{
while(p->rtag==0)p=p->lchild;
printf("%c",p->data);
while(p->rtag==1&&p->rchild!=tb)
{
p=p->rchild;
printf("%c",p->data);
}
p=p->rchild;
}
}
中序遍历算法既没有递归也没有栈,空间效率得到提高
哈夫曼树、并查集
哈夫曼树:设二叉树具有n个带权值的叶子节点,那么从根节点到各个叶子节点的路劲长度与相应节点权值的乘积的和,叫做二叉树的带权路径长度,具有最短带权路径长度的二叉树是哈夫曼树
如图
给定一组数据{1,2,3,3}
则哈夫曼树为
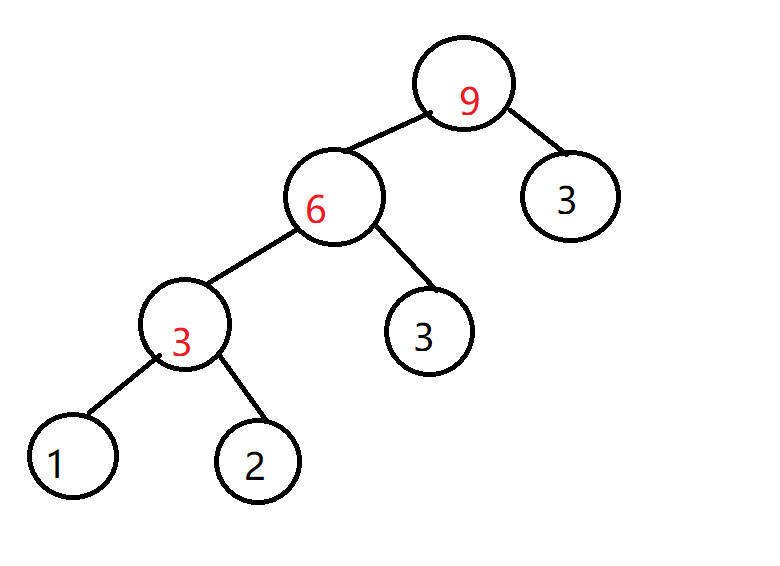
建哈夫曼树的原则就是:保证这棵树拥有最小带权路径长度,即权值越大的夜结点越靠近根节点;权值越小的叶结点越远离根节点
注意:哈夫曼树只存在度为0或2的结点,不存在度为1的结点
哈夫曼树结构体定义
typedef struct
{
char data;
float weight;
int parent;
int lchild;
int rchild;
}HTNode;
哈夫曼编码
在远程通讯中,要将待传字符转换成由二进制的字符串;
编码目标:总编码长度最短
总编码长度最短,用哈夫曼树换个概念就是带权路径长度最短,故建哈夫曼树后,将左分支(右分支)设为0,另一边设为1
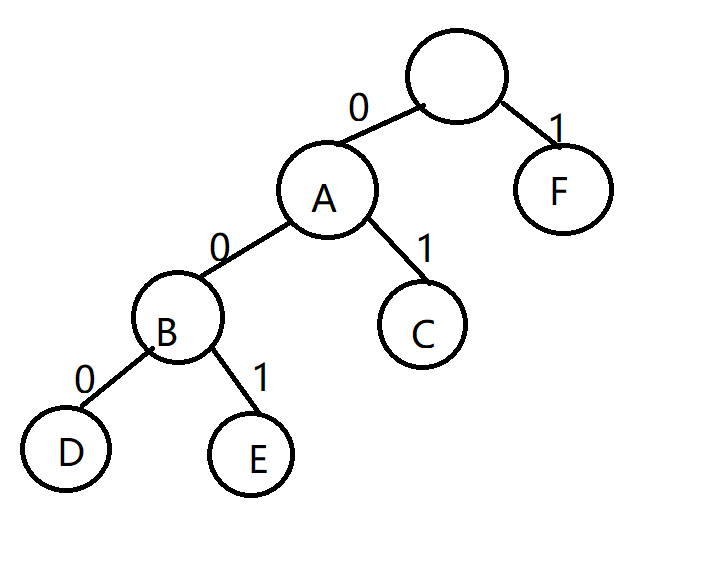
其中A的编码为0,E的编码为001
并查集
查找一个元素所属的集合及合并2个元素各自专属的集合等运算
集合查找:在一棵高度较低的树中查找根节点的编号,所花时间较少。同一个集合标志就是根一样
集合合并:两棵分离集合树A和B,高度分别为ha,hb则若ha>hb,则B为A的子树;
并查集结构体定义
typedef struct node
{
int data;
int rank;
int parent;
}UFSTree;
在查找一个元素所属集合时,当结点值与父亲值相等,则说明已经找到了根节点,返回;
1.2.谈谈你对树的认识及学习体会
认识:树的理解主要在于找到结点与结点间的关系,比如我们的哈夫曼树,就是找最小结点;我们实际中运用树时,其实出现的很少会是特殊的一类,如二叉树,所以结点间的关系往往不只是父节点与孩子结点的关系,还有兄弟结点之间的关系,只有先确定结点之间关系后,我们才能开始构建树;
在哈夫曼编码中,我们了解了树的另一个用途,就是设计编码,同时使编码最短,这也就意味着树在一些安全上有着用处,比如设计编码为一段内容加密,同时并查集的引入让我们知道了合并树的概念,其实并查集最简单的认识就是“等级制度”与“融合”,通过确定上一级来管下一级,而同一级合并到一级,同时不同的关系网能将一级的人数再度扩大;
树其实我们一直都有接触,网页的一些代码就是靠树在实现着
学习体会:树作为一个非线性结构完美体现了它的非线性,一开始的二叉树只是将孩子结点限制在2以内,而树本身一个结点的孩子结点数目是不一定的,所以树的建立真的要考虑很多东西,同时在树这一块,我们开始频繁的见到了递归,这意味着我们必须开始对每一步代码进行细心的检查,因为可能一不小心,递归出口就忘打了;在树这章我们基本将以前学的很多东西都重新开始组合运用,其实树这章内容主要在于对我们以往所学的一个检验,所以对于以前的知识,没有很好的掌握的话这一章学起来确实有点吃力。
2.阅读代码(0--5分)
2.1 另一个子树

class Solution {
public:
bool isSubtree(TreeNode* s, TreeNode* t) {
bool flag = false;
if (s != nullptr && t != nullptr) {
if (s->val == t->val) {
flag = DoesTreeHavaTree(s, t);
}
if (!flag) {
flag = isSubtree(s->left, t);
}
if (!flag) {
flag = isSubtree(s->right, t);
}
}
return flag;
}
bool DoesTreeHavaTree(TreeNode *s, TreeNode *t) {
if (!s && !t) {
return true;
}
if (!s || !t) {
return false;
}
if (s->val != t->val) {
return false;
}
return DoesTreeHavaTree(s->left, t->left) && DoesTreeHavaTree(s->right, t->right);
}
};
2.1.1 该题的设计思路
1.首先寻找根节点相同节点。
先判断根节点是否相等,如果相等,再判断子树是否相等。
否则,判断子树是否等于原树左子树的子树。
否则,判断子树是否等于原树右子树的子树。
2.然后判断子树是否相等
如果都为空,则相等。
如果其中一个不为空,则不等。
如果都不为空,但值不相等,则不等。
递归判断对应左右节点是否相等。
2.1.2 该题的伪代码
定义 flag作为工具变量
if (两个树都不空) {
if (当前结点相等) {
改变flag = DoesTreeHavaTree(s, t);
}
if (flag取反值为0) {
继续向下对比主树左子树
}
if () {
继续向下对比主树左子树
}
}
return flag;
}
bool DoesTreeHavaTree(TreeNode *s, TreeNode *t) {
if (两树都空) {
此时相等
}
if (其中一个树已经空但是另一个没空) {
不相等
}
if (都不空但是当前结点不相等) {
不相等
}
return 对比二者左子树及右子树
}
文字+代码简要介绍本题思路
2.1.3 运行结果
2.1.4分析该题目解题优势及难点。
该题目通过一个变量flag来判断当时两树的情况,优势在于简单易懂,即相等,不相等,空或不空,这些都能通过flag反应,同时随时可以停止判断
难度在于,递归调用太多,而且每一个递归都有下一个递归紧随其后,所以整个代码看下来会有一些吃力,并且因为递归太多,如果不判断好递归出口程序很容易出错
2.2 在二叉树中分配硬币

class Solution {
public:
int distributeCoins(TreeNode* root) {
int moves = 0;
moneyneed(root, moves);
return moves;
}
int moneyneed(TreeNode* root, int &moves) {
if (!root->left && !root->right) {
return root->val - 1;//钱少了就是负数 钱多了就是正数
}
int left = 0, right = 0;
if (root->left) {
left = moneyneed(root->left, moves);
}
if (root->right) {
right = moneyneed(root->right, moves);
}
int res = left + right+ root->val-1;
moves += abs(left)+abs(right);
return res;
}
};
2.2.1 该题的设计思路
通过查看每个结点离所需硬币差多少硬币,通过累计所需硬币(可正可负),累计值就是需要挪动的次数
2.2.2 该题的伪代码
初始化移动次数
调用累计移动函数moneyneed(root, moves);
return moves;
}
int moneyneed(TreeNode* root, int &moves) {
if (左子树与右子树都遍历完毕) {
放回根结点离1硬币的差值
}
定义两个变量统计左右差值
if (左子树未遍历完) {
函数递归调用统计左边所需硬币值
}
if (右子树未遍历完) {
函数递归调用统计右边所需硬币值
}
统计当前左右子树根节点累计值
统计左右子树需要的绝对值
return res;
}
};
2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
优势:该解题方法的思路很巧,每个结点与1相差的绝对值之和就是挪动次数,这样其实代码在统计的是结点值之和,这样程序处理就简单很多,而且这题采用的是后序遍历,这样就避免从根节点开始找时遇到的一些复杂问题
难点:我觉得这题除了思路是难点,方法都很简单
2.3 二叉树寻路

class Solution {
public:
vector<int> pathInZigZagTree(int label) {
int level = log(label) / log(2) + 1; // 计算层数
vector<int> path(level);
while (label) {
path[level-1] = label;
label = pow(2, level) - 1 - label + pow(2, level - 1); // 计算对称点。比如 4 的对称点是 7,7 的对称点是 4, 5 对应 6
label >>= 1;
level--;
}
return path;
}
};
2.3.1 该题的设计思路
该题通过满二叉树的结点特点,左孩子结点2i与右孩子结点2i+1,将所寻找的树一层层向上寻找,去找它的父节点,这样一直向上到根节点,就是路径
2.3.2 该题的伪代码
vector
{
通过满二叉树每层结点个数规律计算寻找结点所在层数
用vector
while (label) {
将当前寻找结点赋给 path[level-1]
计算当前结点的对称点(树为之形,所以结点值时反的)
label=label/2向上一层
level--;
}
return path;
}
};
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
优势:运用满二叉树特点非常方便就找到了上一个结点,同时确定层数,这样就将这个问题变得很简单,整个程序看起来特别简洁
难点:这题的树结点特殊在于之字形,所以父节点找起来并不是很容易,而这题的对称点其实如果往深一点,就是翻转子树,而只是寻找并不翻转就有一点困难
2.4 路径总和 II

class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
vector<vector<int>> ans; vector<int> curr;
if (!root) return ans;
stack<TreeNode*> stk; TreeNode *prev = nullptr;
while (root || !stk.empty()) {
while (root) {
stk.push(root); sum -= root->val; curr.push_back(root->val); //入栈、更新剩余和、路径
root = root->left;
}
root = stk.top();
if (!root->left && !root->right && (sum == 0)) {
ans.push_back(curr);
}
if (!root->right || root->right == prev) {
stk.pop(); sum += root->val; curr.pop_back();
prev = root;
root = nullptr;
}
else {
root = root->right;
}
}
return ans;
}
###2.4.1 该题的设计思路
申请两个动态数组,一个存放所有路径,一个存放当前路径,从根节点开始往下一个个找,通过用和减去当前结点判断路径是否满足条件,满足则存入满足路径数组,不满足则回溯到上一个结点后向另一边遍历,再不符合则再回溯到已经回溯过的结点的上一层,直到找到所有路径
###2.4.2 该题的伪代码
vector<vector<int>> pathSum(TreeNode* root, int sum) {
定义两个动态数组分别记录所有满足条件的路径以及一条满足条件的路径
if (树空) 返回 路径;
定义一个栈存储结点值;
定义一个树结构prev方便回溯
while (树不空或栈不空) { //模拟系统递归栈
while (树不空) {
将当前树节点入栈;
修改和为减去当前结点值;
记录结点进路径数组
递归访问左结点
}
左子树空,树取栈顶往右走
if (是叶子结点且剩余和为0) {
保存路径
}
if (右结点不存在或已经访问 回溯) { //右结点不存在或已经访问 回溯
出栈、更新剩余和、取出路径最后一个值
prev = root; //标记已访问
root = nullptr; //用于回溯到上一级
}
else {
递归访问右结点
}
}
return ans;
}
};
###2.4.3 运行结果
###2.4.4分析该题目解题优势及难点。
优势:本题类似于找迷宫出口,回溯法和栈的使用使路径随时更新,同时动态数组的存在很容易将不符合的路径值除去。
难点:回溯法修改比较困难,同时因为需要对三个变量进行实时修改,所以需要精确把握每一步


 浙公网安备 33010602011771号
浙公网安备 33010602011771号