TPR、FPR、precision、recall、accuracy、ROC、AUC
| 真实值：1 | 真实值：0 | |
| 预测值：1 | TP | FP |
| 预测值：0 | FN | TN |
真阳率(True positive)：$TPr=\frac{ TP}{(TP+FN)} $真正的1中，被预测为1的比例
假阳率(False positive)：$FPr= \frac{FP}{(FP+TN)}$ 真正的0中，被预测为1的比例
精确率(Precision)：$Precision = \frac{TP}{(TP+FP)} $预测出来的1中，真正为1的比例
召回率(Recall)：$Recall = \frac{TP}{(TP+FN) }$真正的1中，被预测为1的比例
准确率(Accuracy)：$Accuracy = \frac{(TP+TN)}{(TP+FN+FP+TN)}$所有样本中能被正确识别为0或者1的概率
1.ROC 曲线
因为预测出来的评分需要有一个阈值，擦能把他划分为1或者0.
一个阈值对应一组（TPr,FPr），多个阈值就能够得到多组（TPr,FPr），就能得到ROC曲线.
我们希望一组（TPr,FPr）中，TPr越大越好，FPr越小越好
sklearn代码如下：
import numpy as np from sklearn import metrics y = np.array([1, 1, 2, 2]) scores = np.array([0.1, 0.4, 0.35, 0.8]) fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2) print(fpr, tpr, thresholds)
# [0. 0. 0.5 0.5 1. ] [0. 0.5 0.5 1. 1. ] [1.8 0.8 0.4 0.35 0.1 ]
y = np.array([0, 0, 1, 1])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores)
print(fpr, tpr, thresholds)
# [0. 0. 0.5 0.5 1. ] [0. 0.5 0.5 1. 1. ] [1.8 0.8 0.4 0.35 0.1 ]
因为真实的标签使用{1,2}来区分的，所以需要用pos_label=2来制定2是正类的标签。
如果你的数据标签是{0,1}或者{-1,1}，那么可以不用指定pos_label。
（很容易看到：如果阈值取大于0.8的数，那么TPr=FPr=0。sklearn可能是默认取了最高分0.8+1，所以阈值才会出现1.8）
阈值是自动从最高分[1.8 0.8 0.4 0.35 0.1 ]依次往下取的。
大于等于阈值，预测为1.
| 不同阈值时的预测标签 | ||||||
| 真实标签y | 得分scores | 阈值=1.8 | 阈值=0.8 | 阈值=0.4 | 阈值=0.35 | 阈值=0.1 |
| 1 | 0.8 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0.35 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0.4 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0.1 | 0 | 0 | 0 | 0 | 1 |
当阈值=1.8: TP=0,FP=0,FN=2,TN=2;所以tpr=0， fpr=0.
当阈值=0.8: TP=1,FP=0,FN=1,TN=2;所以tpr=0.5， fpr=0.
当阈值=0.4: TP=1,FP=1,FN=1,TN=1;所以tpr=0.5， fpr=0.5.
当阈值=0.35: TP=2,FP=1,FN=0,TN=1;所以tpr=1， fpr=0.5.
当阈值=0.1: TP=2,FP=2,FN=0,TN=0;所以tpr=1， fpr=1.
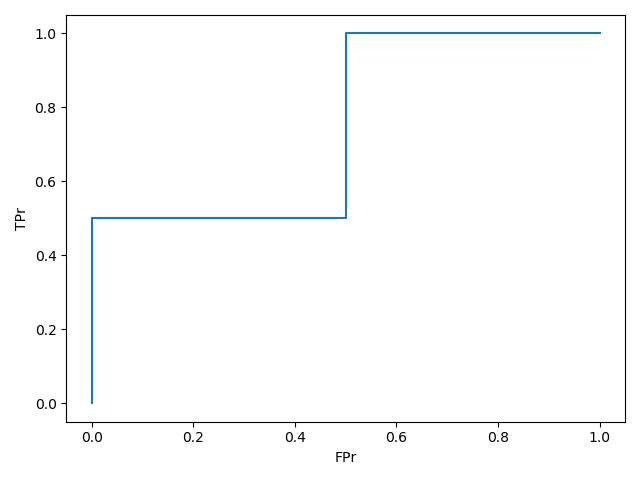
五组（fpr,tpr）数据，把他们连起来就得到了ROC曲线
实际中，阈值的取值非常多，所以roc曲线更加光滑
2.AUC
AUC值就是ROC曲线下面的面积，怎么计算呢？
方法一：可以采用积分方法求得面积，不过未免有些麻烦。
方法二：sklearn.metrics.roc_auc_score（或者sklearn.metrics.auc）可以计算AUC，但是需要通过“真实标签y_true”和“模型预测得到的概率y_scores”来计算的。
roc_auc_score直接根据标签y和预测概率得分scores计算得到AUC的值
sklearn.metrics.auc唏嘘通过roc_curve先得到fpr, tpr作为输入。
import numpy as np from sklearn.metrics import roc_auc_score,auc y = np.array([0, 0, 1, 1]) scores = np.array([0.1, 0.4, 0.35, 0.8]) auc1 = roc_auc_score(y, scores) fpr, tpr, thresholds = roc_curve(y, scores) auc2 = auc(fpr, tpr) print(auc1,auc2)
auc1 = 0.75
auc2 = 0.75
计算方法：计算（正样本预测得分大于负样本预测得分）的组数。
''' 1 0.9 1 0.8 1 0.3 0 0.2 0 0.4 正样本个数*负样本个数=3*2 = 6 第一个正样本预测为0.9,0.9大于负样本预测出来的0.2和0.4，所以计数为2 第一个正样本预测为0.8,0.9大于负样本预测出来的0.2和0.4，所以计数为2 第一个正样本预测为0.3,0.9大于负样本预测出来的0.2，所以计数为1 2+2+1 = 5 所以auc=5/6，auc>0.7都可以运用到线上生产环境 '''
方法三：快速计算方法。
方法二中需要比较每一个正样本和每一个负样本之间的预测概率大小，这是非常麻烦的。设正样本数目为n1，负样本数目为n0.按照得分从小到大排列所有的正负样本。然后采用下面说的方法来计算AUC值（转）。
3. AP
点击查看官方文档说明
公式：$AP = \sum_{n}{(R_{n}-R_{n-1})P_{n}}$
这儿涉及到了两个函数
1.precision_recall_curve、可以求得不同阈值下的precision和recall，
2.average_precision_score，AP就是通过这个函数求得
precision_recall_curve得到了precision和recall，还便于我们可以手动计算，验证average_precision_score的计算结果。
import numpy as np from sklearn.metrics import precision_recall_curve y_true = np.array([0, 0, 1,1]) y_scores = np.array([0.1, 0.4, 0.35, 0.8]) precision, recall, thresholds = precision_recall_curve(y_true, y_scores)# stop when full recall attained print(precision,recall,thresholds) a_p_s = average_precision_score(y_true, y_scores) print("aps=",a_p_s)
precision=[0.66666667 0.5 1. 1. ]
recall = [1. 0.5 0.5 0. ]
thresholds = [0.35 0.4 0.8 ] aps= 0.8333333333333333
注意到为什么thresholds的结果为[0.35 0.4 0.8 ]，为什么没了0.1，也没了1.8.（因为在metrics.roc_curve(y, scores)我们看到thresholds的结果为[0.1, 0.35, 0.4, 0.8, 1.8]含有0.1和1.8）
文档这么写的：
The last precision and recall values are 1. and 0. respectively and do not have a corresponding threshold. This ensures that the graph starts on the y axis.
我们可以理解到：之所以1.8没了,因为直接把最高分0.8当成阈值。并且在precision和recall对应的列表分别添加了“1”、“0”
为什么最小阈值0.1也没了呢，注意看在代码注释处这样写道
# stop when full recall attained # and reverse the outputs so recall is decreasing
所以说可能是在阈值为0.35的时候，召回率recall已经为1.我们来验证一下：
当阈值=0.35: TP=2,FP=1,FN=0,TN=1; recall = TP/(TP+FN)=1,precision=TP/(TP+FP)=2/3=0.6667
当阈值=0.1: TP=2,FP=2,FN=0,TN=0; recall = TP/(TP+FN)=1,precision=TP/(TP+FP)=1/2=0.5
可以看到当阈值=0.35的时候，recall确实已经为1.
我们换一组数据尝试一下，看看到底是recall=1就停止了，还是说最小的阈值没有考虑：
import numpy as np from sklearn.metrics import precision_recall_curve y_true = np.array([0, 0, 1,1]) y_scores = np.array([0.5, 0.4, 0.35, 0.8]) precision, recall, thresholds = precision_recall_curve(y_true, y_scores)# stop when full recall attained print(precision,recall,thresholds) a_p_s = average_precision_score(y_true, y_scores) print("aps=",a_p_s)
precision = [0.5 0.33333333 0.5 1. 1. ]
recall = [1. 0.5 0.5 0.5 0. ]
thresholds = [0.35 0.4 0.5 0.8 ] aps= 0.75
发现输出了所有的阈值（除了1.8）：thresholds = [0.35 0.4 0.5 0.8 ]。
说明precision_recall_curve函数，
1.是从预测结果的最高分作为阈值开始计算的precision和recall，当recall=1，就停止了计算
2.并且在precision和recall对应的列表分别添加了“1”、“0”
a.在第一组数据中
precision=[0.66666667 0.5 1. 1. ]
recall = [1. 0.5 0.5 0. ]
thresholds = [0.35 0.4 0.8 ] aps= 0.8333333333333333
根据公式来计算一下：
AP=(1-0.5)*0.666667+(0.5-0.5)*0.5+(0.5-0)*1=0.83333333333=aps
b.在第二组数据中
precision = [0.5 0.33333333 0.5 1. 1. ]
recall = [1. 0.5 0.5 0.5 0. ]
thresholds = [0.35 0.4 0.5 0.8 ]
aps = 0.75
根据公式计算一下：
AP = (1-0.5)*0.5 + (0.5-0.5)*0.33333 +(0.5-0.5)*0.5 + (0.5-0)*1 = 0.75
4.precision,recall,accuracy
from sklearn.metrics import recall_score,precision_score, accuracy_score y_true = [0, 1, 1, 0, 1, 0,1,1] y_pred = [0, 1, 1, 1, 0, 0,0,1] precision =precision_score(y_true, y_pred) # doctest: +ELLIPSIS recall =recall_score(y_true, y_pred) accuracy = accuracy_score(y_true, y_pred) print(precision, recall, accuracy) # 0.75 0.6 0.625
真实标签 y_true = [0, 1, 1, 0, 1, 0, 1, 1]
预测标签 y_pred = [0, 1, 1, 1, 0, 0， 0，1]
TP = 3 FP = 1
FN = 2 TN = 2
所以precision = TP/(TP+FP)=3/4=0.75
racall = TP/(TP+FN)=3/5=0.6
accuracy = (TP+TN)/(TP+FP+FN+TN)=5/8=0.625
