推荐系统——FFM模型点击率CTR预估（代码，数据流动详细过程）
前言：主要记录，在推荐系统利用FFM模型，进行CTR预估的时候，离散化特征需要嵌入，field之间的特征交叉是怎么计算的？记录了数据流动的每一个过程。
FMM是在FM的基础上改进的，理论部分未作过多解释。（内容有不足之处，请大家指正批评）
参考：github：pytorch-fm
一、公式：
FFM模型定义如下：
class FieldAwareFactorizationMachineModel(torch.nn.Module): def __init__(self, field_dims, embed_dim): super().__init__() self.linear = FeaturesLinear(field_dims) self.ffm = FieldAwareFactorizationMachine(field_dims, embed_dim) def forward(self, x): """ :param x: Long tensor of size ``(batch_size, num_fields)`` """ ffm_term = torch.sum(torch.sum(self.ffm(x), dim=1), dim=1, keepdim=True) x = self.linear(x) + ffm_term return torch.sigmoid(x.squeeze(1))
self.linear 是为了求出
self.ffm是为了求出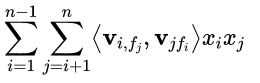
self.linear(x) + ffm_term表示两部分相加
设样本有三个field，num_dield = 3，field1取值有10种情况，field2取值有20种情况，field3取值有10种情况
那么field_dims=[10,20,10],令嵌入维度embed_dim=4
在forward中，由于一次读取的是batch_size个数据，设batch_size=5
那么x = [[1,3,1], [1,7,1], [2,10,2], [3,10,3], [4,11,2]] x的shape为：batch_size*num_field=5*3
二、FeaturesLinear(field_dims)
接下来看一下FeaturesLinear(field_dims)是怎么实现的
class FeaturesLinear(torch.nn.Module): def __init__(self, field_dims, output_dim=1): super().__init__() self.fc = torch.nn.Embedding(sum(field_dims), output_dim) self.bias = torch.nn.Parameter(torch.zeros((output_dim,))) self.offsets = np.array((0, *np.cumsum(field_dims)[:-1]), dtype=np.long) def forward(self, x): """ :param x: Long tensor of size ``(batch_size, num_fields)`` """ print("FeaturesLinear x=",x) x = x + x.new_tensor(self.offsets,dtype=np.long).unsqueeze(0) print("FeaturesLinear return=", torch.sum(self.fc(x), dim=1) + self.bias) return torch.sum(self.fc(x), dim=1) + self.bias
sum(field_dims) = 10+20+10 = 40, output_dim嵌入维度默认为1
self.fc = torch.nn.Embedding(sum(field_dims), output_dim)相当于构建了一个索引字典，索引为1到40，每个索引对应一个长度为output_dim=1的向量
bias就是公式中的w0
为什么需要self.offsets，是这样的：
以样本[1,3,1]为例，one-hot编码过后其实是
[1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0]
那么“1”所在的位置对应的索引分别为1、13、31.那该怎么得到这个索引呢，offsets发挥作用了，
因为eg filed_dims=[10, 20,10],那麽offsets=[0,10,30]，把[1, 3, 1] + [0, 10, 20] = [1, 13, 31]
因为输入的x = [[1,3,1], [1,7,1], [2,10,2], [3,10,3], [4,11,2]]
所以通过加上offsets之后 x变为了[1,13,31],[1,17,31],[2,20,32],[3,20,33],[4,21,32]]
self.fc(x)的会得到一个batch_size*num_field*output_dim的tensor（不清楚可以查看pytorch中embdding的用法）, 它长这样：
tensor([[[-0.3187], [-0.1316], [ 0.1061]], [[-0.3187], [ 0.1420], [ 0.1061]], [[-0.2323], [ 0.1549], [ 0.2619]], [[ 0.2500], [ 0.1549], [ 0.0837], [[ 0.1705, [ 0.2401], [ 0.2619]]]
[1,13,31]对应[[-0.3187], [-0.1316], [ 0.1061]],大小为num_filed*output_dim=3*1
[1,17,31]对应[[-0.3187], [ 0.1420], [ 0.1061]],大小为num_filed*output_dim=3*1
torch.sum(self.fc(x), dim=1)得到一个batch_size*output_dim大小的张量：
对于[1,13,31]就是把[[-0.3187], [-0.1316], [ 0.1061]]第dim=1维的数据相加.
变成为[-0.3187]+[-0.1316]+ [0.1061]=[-0.3534]
所以torch.sum(self.fc(x), dim=1)的结果为
[[-0.3534], [*], [*], [*], [*]] # 后面四个*值自己加
最后加上bias
三、FieldAwareFactorizationMachine(field_dims, embed_dim)
看看FieldAwareFactorizationMachine(field_dims, embed_dim)是怎么实现的
field_dims=[10, 20, 10], 设embed_dim=4
x+offsset = [1,13,31],[1,17,31],[2,20,32],[3,20,33],[4,21,32]]
class FieldAwareFactorizationMachine(torch.nn.Module): def __init__(self, field_dims, embed_dim): super().__init__() self.num_fields = len(field_dims) self.embeddings = torch.nn.ModuleList([ torch.nn.Embedding(sum(field_dims), embed_dim) for _ in range(self.num_fields) ]) self.offsets = np.array((0, *np.cumsum(field_dims)[:-1]), dtype=np.long) for embedding in self.embeddings: torch.nn.init.xavier_uniform_(embedding.weight.data) def forward(self, x): """ :param x: Long tensor of size ``(batch_size, num_fields)`` """ x = x + x.new_tensor(self.offsets, dtype=np.long).unsqueeze(0) xs = [self.embeddings[i](x) for i in range(self.num_fields)] ix = list() for i in range(self.num_fields - 1): for j in range(i + 1, self.num_fields): ix.append(xs[j][:, i] * xs[i][:, j]) ix = torch.stack(ix, dim=1)
self.embeddings = torch.nn.ModuleList([
torch.nn.Embedding(sum(field_dims), embed_dim) for _ in range(self.num_fields)
])
因为在FFM中，每一维特征 xi，针对其它特征的每一种field fj，都会学习一个隐向量 v_i,fj，所以有多少个field们就要构建多少个torch.nn.Embedding层
（不太会用术语解释，相当于总的特征为sum(field_dims)=40, 嵌入维度embed_dim=4，共有num_field=3个field，所以就要构建3个embedding，
当i=1，f_{j}=2，得到v_{1,2},表示特征1对第2个field的一个长度为4的向量）
offset的作用和上文提到的一样
torch.nn.init.xavier_uniform_(embedding.weight.data)是一种初始化嵌入层权重的方法
xs = [self.embeddings[i](x) for i in range(self.num_fields)]
将会的到长度为num_field=3的列表，列表中的每一个元素，大小都为batch_size*num_field*embed_dim=5*3*4
形如：（[1,13,31],[1,17,31],[2,20,32],[3,20,33],[4,21,32]]）
列表的第1个元素分别记录着当前batch中的所有样本各自的特征对第1个field1的隐向量
列表的第2个元素分别记录着当前batch中的所有样本各自的特征对第2个field2的隐向量
列表的第3个元素分别记录着当前batch中的所有样本各自的特征对第3个field3的隐向量
FieldAwareFactorizationMachine_xs=
[tensor([[[-0.3187, -0.2215, 0.2950, -0.2186], # 特征“1”对field1的隐向量 [-0.1316, 0.1353, 0.3162, 0.0994], # 特征“13”对field1的隐向量 [ 0.1061, 0.0932, -0.3512, -0.2172]], # 特征“31”对field1的隐向量
# 记录着第一个样本[1,13,31]的“1”号，“13”号、“31”特征对第一个field1的隐向量 [[-0.3187, -0.2215, 0.2950, -0.2186], # 特征“1”对fieled1的隐向量 [ 0.1420, -0.0538, -0.2896, -0.1630], # 特征”17“对field1的隐向量 [ 0.1061, 0.0932, -0.3512, -0.2172]], # 特征“31”对field1的隐向量
# 记录着第二个样本[1, 17, 31]的“1”号、“17”号、“31”号特征对第一个filed1的影响量” [[-0.2323, -0.0702, 0.1226, -0.0558], [ 0.1549, 0.3265, 0.1930, -0.0248], [ 0.2619, -0.2355, -0.1781, 0.1442]], [[ 0.2500, -0.2571, -0.3023, 0.2887], [ 0.1549, 0.3265, 0.1930, -0.0248], [ 0.0837, 0.1860, 0.0337, -0.3686]], [[ 0.1705, 0.1915, 0.2721, 0.0653], [ 0.2401, 0.3042, 0.1146, 0.3081], [ 0.2619, -0.2355, -0.1781, 0.1442]]],
grad_fn=<EmbeddingBackward>),
tensor([[[-0.2026, 0.0910, -0.1647, -0.0428], # 特征“1”对field2的隐向量 [ 0.1085, 0.2459, 0.2358, -0.0501], # 特征“13”对field2的隐向量 [ 0.2694, 0.0325, 0.2198, 0.2486]], # 特征“31”对field2的隐向量
# 记录着第一个样本[1, 13, 31]的“1”号、“13”号、“31”号特征对field2的隐向量 [[-0.2026, 0.0910, -0.1647, -0.0428], [ 0.1493, 0.2111, 0.0914, -0.1304], [ 0.2694, 0.0325, 0.2198, 0.2486]], [[ 0.0288, -0.3006, 0.0826, 0.3179], [-0.1215, -0.3026, -0.2408, -0.2218], [-0.1306, -0.2992, -0.2194, -0.3114]], [[ 0.2275, -0.0470, 0.0298, 0.0510], [-0.1215, -0.3026, -0.2408, -0.2218], [ 0.0844, -0.3333, 0.3446, -0.0249]], [[-0.3259, -0.0525, 0.2875, -0.2050], [ 0.2183, 0.0466, 0.3299, 0.1833], [-0.1306, -0.2992, -0.2194, -0.3114]]], grad_fn=<EmbeddingBackward>),
tensor([[[-0.0756, -0.1417, 0.0075, 0.0632], # 特征“1”对field3的隐向量 [-0.0770, 0.2010, 0.0051, 0.0050], # 特征“13”对field3的隐向量 [-0.1394, 0.0776, 0.2685, -0.1017]], # 特征“31”对field3的隐向量
# 记录着第一个样本[1, 13, 31]的“1”号、“13”号、“31”号特征对field3的隐向量 [[-0.0756, -0.1417, 0.0075, 0.0632], [-0.1809, 0.0321, 0.1205, 0.1586], [-0.1394, 0.0776, 0.2685, -0.1017]], [[-0.3561, 0.2795, 0.3210, -0.0522], [-0.1674, 0.1584, 0.1336, 0.1036], [-0.0826, 0.2853, 0.2323, 0.1982]], [[ 0.0778, -0.3036, -0.1546, 0.2859], [-0.1674, 0.1584, 0.1336, 0.1036], [ 0.2655, 0.1352, 0.0962, 0.1214]], [[-0.0497, 0.1356, 0.0720, 0.0554], [-0.1741, -0.0329, -0.3503, -0.0485], [-0.0826, 0.2853, 0.2323, 0.1982]]], grad_fn=<EmbeddingBackward>)]
注意以下代码就是求：
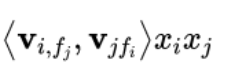
ix = list() for i in range(self.num_fields - 1): for j in range(i + 1, self.num_fields): ix.append(xs[j][:, i] * xs[i][:, j])
按理说一共有40个特征，为什么循环是这样写的，好像应该这样
i取1，j应该取2到40；
i取2，j应该取3到40；
……
i取39，j应该取40；
# 注意：FFM模型中不同field的特征之间，eg：“1”与"9"不交叉，因为1,和9属于[1,2,……,10]在同一field1。同理[11,12,……,30]field2之间不交叉，[31,32,……,40]field3之间不交叉
# 考虑field1、field2、field3之间互相交叉
# 以第一个样本[1,13,31]为例，虽然每个embeddings[i]层都有[1,2,……,40]的嵌入向量
# 但是[1,13,31]只有这1、13、31这三个位置的值不为0，就算1与20交叉过后，v_{1,f_{20}}*v_{20,f_{1}}*x_{1}*x_{20}=0，对最终的计算结果没有贡献
# 就只考虑了1,13，和31之间的相互交叉
# 所以我们要计算的就是x1与x13、x1与x31，x13与x31之间的交叉，得到的交叉特征共有3项。field1*field2；field1*field3；field2*field3；
（如果，num_field=4的话，交叉特征共有6项：field1*field2；field1*field3；field1*field4；field2*field3；field2*field4；field3*field4；）
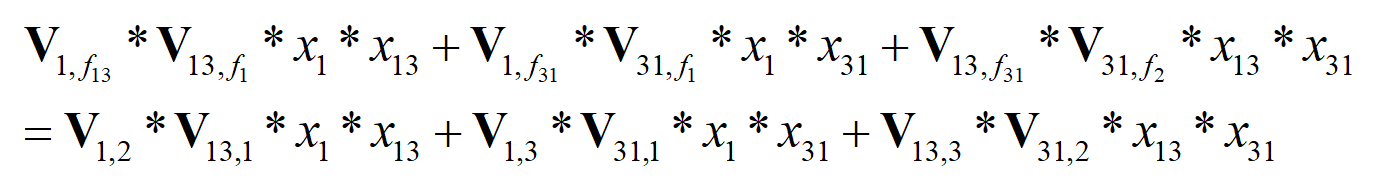
通过FieldAwareFactorizationMachine_xs的结果我们可以看到，第一个样本的特征对field1、field2、field3的隐向量分别为
[[-0.3187, -0.2215, 0.2950, -0.2186], # 特征“1”对field1的隐向量 [-0.1316, 0.1353, 0.3162, 0.0994], # 特征“13”对field1的隐向量 [ 0.1061, 0.0932, -0.3512, -0.2172]], # 特征“31”对field1的隐向量 [[-0.2026, 0.0910, -0.1647, -0.0428], # 特征“1”对field2的隐向量 [ 0.1085, 0.2459, 0.2358, -0.0501], # 特征“13”对field2的隐向量 [ 0.2694, 0.0325, 0.2198, 0.2486]], # 特征“31”对field2的隐向量 [[-0.0756, -0.1417, 0.0075, 0.0632], # 特征“1”对field3的隐向量 [-0.0770, 0.2010, 0.0051, 0.0050], # 特征“13”对field3的隐向量 [-0.1394, 0.0776, 0.2685, -0.1017]], # 特征“31”对field3的隐向量
V(1,2)是“1”号特征对field2的隐向量，对应数据[-0.2026, 0.0910, -0.1647, -0.0428]
V(13,1)是“13”号特征对field1的隐向量，对应数据[-0.1316, 0.1353, 0.3162, 0.0994]
ix最终得到的结果是一个长度为3（这个3是交叉特征的数目，不是num_field的数目）的列表
[tensor([[ 0.0267, 0.0123, -0.0521, -0.0043], # [-0.0288, -0.0049, 0.0477, 0.0070], # [ 0.0045, -0.0982, 0.0159, -0.0079], # [ 0.0352, -0.0154, 0.0057, -0.0013], # [-0.0783, -0.0160, 0.0329, -0.0632]], grad_fn=<MulBackward0>), tensor([[-0.0080, -0.0132, -0.0026, -0.0137], # [-0.0080, -0.0132, -0.0026, -0.0137], # [-0.0933, -0.0658, -0.0572, -0.0075], # [ 0.0065, -0.0565, -0.0052, -0.1054], # [-0.0130, -0.0319, -0.0128, 0.0080]], grad_fn=<MulBackward0>), tensor([[-0.0207, 0.0065, 0.0011, 0.0012], # [-0.0487, 0.0010, 0.0265, 0.0394], # [ 0.0219, -0.0474, -0.0293, -0.0323], # [-0.0141, -0.0528, 0.0460, -0.0026], # [ 0.0227, 0.0099, 0.0768, 0.0151]], grad_fn=<MulBackward0>)]
[ 0.0267, 0.0123, -0.0521, -0.0043] 表示
，特征“1”和特征“13”交叉
我们来验证一下：
V(1,2)*V(13,1) =[-0.2026, 0.0910, -0.1647, -0.0428].*[-0.1316, 0.1353, 0.3162, 0.0994] =[ 0.0267, 0.0123, -0.0521, -0.0043] # 是正确的
同理：
[-0.0080, -0.0132, -0.0026, -0.0137]表示，特征“1”和特征“31”交叉
[-0.0207, 0.0065, 0.0011, 0.0012]表示，特征“13”和特征“31”交叉
分别记录着[1, 13, 31]这个样本，特征交叉过后的结果
再进行一次
ix = torch.stack(ix, dim=1)
得到的结果为（这就是第一部分，FieldAwareFactorizationMachineModel中self.ffm(x）的返回值)：
#tensor( # [[[ 0.0267, 0.0123, -0.0521, -0.0043], # [-0.0080, -0.0132, -0.0026, -0.0137], # [-0.0207, 0.0065, 0.0011, 0.0012]], # # [[-0.0288, -0.0049, 0.0477, 0.0070], # [-0.0080, -0.0132, -0.0026, -0.0137], # [-0.0487, 0.0010, 0.0265, 0.0394]], # # [[ 0.0045, -0.0982, 0.0159, -0.0079], # [-0.0933, -0.0658, -0.0572, -0.0075], # [ 0.0219, -0.0474, -0.0293, -0.0323]], # # [[ 0.0352, -0.0154, 0.0057, -0.0013], # [ 0.0065, -0.0565, -0.0052, -0.1054], # [-0.0141, -0.0528, 0.0460, -0.0026]], # # [[-0.0783, -0.0160, 0.0329, -0.0632], # [-0.0130, -0.0319, -0.0128, 0.0080], # [ 0.0227, 0.0099, 0.0768, 0.0151]]], grad_fn=<StackBackward>)
第一个样本最终交叉特征的结果就汇总记录到了
# [[ 0.0267, 0.0123, -0.0521, -0.0043],
# [-0.0080, -0.0132, -0.0026, -0.0137],
# [-0.0207, 0.0065, 0.0011, 0.0012]]
四、两部分相加
现在linear部分和交叉特征ffm部分的结果都得到了，回到代码，我们看看他是怎么相加的，（黑体下划线的代码）
class FieldAwareFactorizationMachineModel(torch.nn.Module): def __init__(self, field_dims, embed_dim): super().__init__() self.linear = FeaturesLinear(field_dims) self.ffm = FieldAwareFactorizationMachine(field_dims, embed_dim) def forward(self, x): """ :param x: Long tensor of size ``(batch_size, num_fields)`` """ ffm_term = torch.sum(torch.sum(self.ffm(x), dim=1), dim=1, keepdim=True) x = self.linear(x) + ffm_term return torch.sigmoid(x.squeeze(1))
我们可以看到ffm_term将会得到一个batch_size*1的tensor
而 self.linear(x)得到是batch_size*output_dim=5*1的tensor
两部分可以直接相加，最后消除x长度为1的维度x.squeeze(1)，
在经过一个sigmoid，就得到了大小为batch_size的一个tensor，tensor中的每一个元素都在0到1之间，这就是这屋个样本模型计算出来是否会被点击的概率。
然后根据他们真实的标签“1”或者“0”，计算logloss就可以了，这样一个batch_size的计算过程就结束了。
不清楚的地方或不足之处，请留言互相交流。
1, 17, 31
