寻找两个有序数组的中位数

原题目：

　　给定两个大小为m，n的有序数组nums1和nums2，找出这两个有序数组的中位数，要求时间复杂度为O(log(m+n)).

　　eg:nums1=[1,3];nums2=[2];中位数是2.0

　　nums1=[1,2];nums2=[3,4];中位数是(2+3)/2=2.5

不考虑时间复杂度，简单做法就是把nums1和nums2两个数组的并集重新排序，取得中位数。

 

基本思想：
需要求的中位数mid是把两个数组并集构成的数组num3的元素分为数目相等的两部分。设小于mid的元素构成集合C。
计算两个数组元素总长度sumLen
需要向C中添加的元素长度为(sumLen+1)/2 向下取整

   最开始仍需要添加到C中元素的长度为want=(sumLen+1)/2 向下取整，取索引值为indexa=indexb=want/2;

 

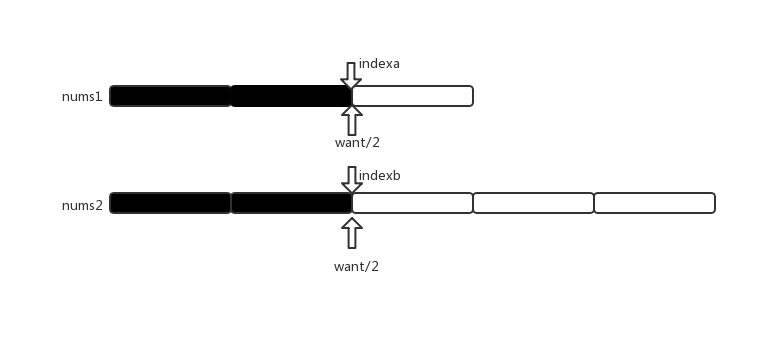
比较nums1[indexa]与nums2[indexb]的大小(谁数值大，谁索引二分)，假设nums1[indexa]<nums2[indexb]，就对nums2再次进行二分找元素,直到nums1[indexa]>nums2[indexb]，

假设indexb连续二分两次过后（indexb=indexb/2），nums1[indexa]>nums2[indexb]，

  　　　　然后把nums1索引z为indexa和indexa之前的indexa+1个元素和nums2索引为indexb和indexb之前的indexb+1个元素添加到数组C中，

 

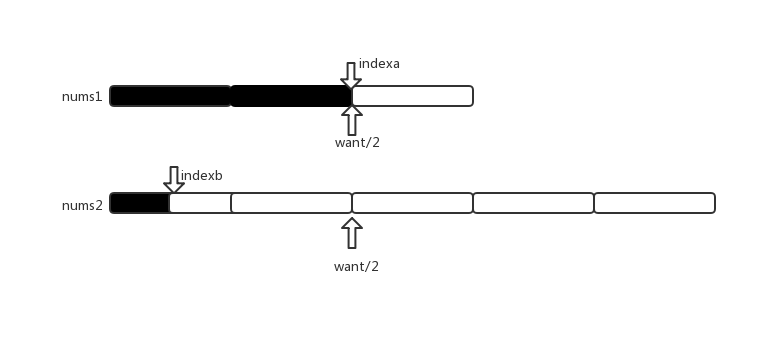
更新want的值，计算want=(sumLen+1)/2-indexa-1-indexb-1。

记录上一次indexa和indexb的值为，indexa1=indexa，indexb1=indexb

更新indexa，indexb，indexa=indexa1+want/2,indexb=indexb+want/2

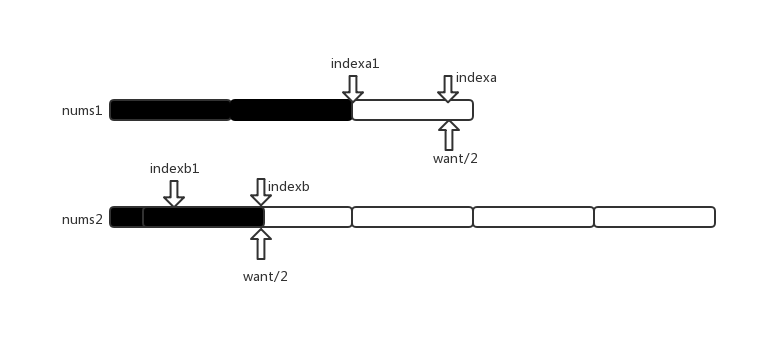
假设nums1[indexa]还是小于nums2[indexb]，就对nums2再次进行二分找元素,直到nums1[indexa]>nums2[indexb]，

假设indexb一次二分过后，nums1[indexa]>nums2[indexb]，然后把nums1索引为indexa1之后和indexa之前的元素（左开右闭）和nums2索引为indexb1之后和indexb之前的元素（左开右闭）添加到数组C中，

 

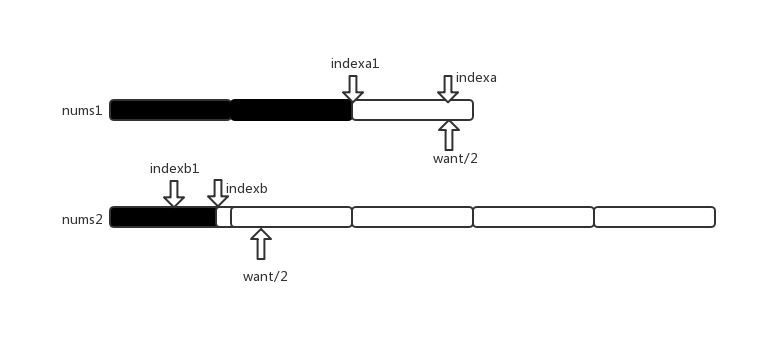
重复做下去，直到indexa+1+indexb+1 = sumLen/2

　　如果sumLen为奇数，说明nums[index+1]与nums2[indexb+1]两个元素较小的那个元素就是最终数组nums3的中位数,结束。

　　如果sumLen为偶数，记录nums[indexa]与nums[indexb]中较大的值为c1，记录nums[indexa+1]与nums[indexb+1]中较小的值为c2，最终数组nums3的中位数为(c1+c2)/2

思路：
假设两个数组nums1与nums2都不为空（其中一个数组为空就比较简单）
第零步：计算两个数组的总长度sumLen=nums1.length+nums2.length
    int indexa=-1,indexb=-1;
    int indexa1=-1,,indexb1=-1;
    设nums1与nums2合并后得到的数组为nums3，nums3中位数之前的元素构成数组C，C最终的的长度为(sumLen+1)/2
    计算仍需向数组C添加元素的个数为want(最开始want=(sumLen+1)/2-indexa-1-indexb-1)，
第一步：判断两个数组的中位数是否相等？
    相等，两个有序数组的中位数就是原来各自数组的中位数。
    不相等，进入第二步。
第二步：

    从nums1和nums2中各自取出indexa和indexb后面的want/2个元素进行比较（这儿需要判断indexa和indexb后面总数组元素长度和want/2的大小关系），再计算indexa或者indexb
    //更新indexa与indexb的值
    if(nums1.length-1<indexa+want/2){//eg: 0,9 1,7 2,3 3,2 4,4。length=5 want/2=5，indexa=-1,不满足，直接进入第三种情况
        indexb=indexb+want-(nums1.length-1-indexa);//当indexa=nums1.length-1;indexb=indexb+want;
        indexa=nums1.length-1;
    }else if( (indexb+want/2) > (nums2.length-1)){
        indexa=indexa+want-(nums2.length-1-indexb);
        indexb=nums2.length-1;
    }else{
        indexa=indexa+want/2; indexb=indexb+want/2;
    }
        


第三步：比较nums1[indexa]与nums2[indexb]的大小(谁大谁二分)，
    ①如果，nums1[indexa]<nums2[indexb]，就对nums2再次进行二分找元素(if indexb=indexb1+1,indexb=indexb1,else indexb=(indexb-indexb1+1)/2-1)，直到nums1[indexa]>nums2[indexb]，
        ①退出循环时，当indexb>=indexb1+1,证明能找到一个nums2[indexb]，然后把nums1索引为indexa1+1到indexa的indexa+1个元素和nums2索引为indexb+1到indexb的indexb+1个元素添加到数组C中，
            计算want=(sumLen+1)/2-indexa-1-indexb-1。
            更新indexa1，indexb1；indexa1=indexa;indexb1=indexb;
        ②退出循环时，当indexb=indexb1，说明nums1[indexa]小于等于nums2还没有添加到C中的那部分元素的第一个元素，就把nums1数组的nums1[indexa1+1]到nums1[indexa]之前的元素添加到C中，
            计算want=(sumLen+1)/2-indexa-1-indexb-1.
            更新indexa1，indexb1；indexa1=indexa;indexb1=indexb;
    ②如果，nums2[indexb]<nums1[indexa]，就对nums1再次进行二分查找元素,同理。
第四步：判断sumLen的奇偶性
    ①如果sumLen为奇数，判断indexa+1+indexb+1与(sumLen-1)/2大小，或者与sumLen/2的大小，因为奇数时，(sumLen-1)/2=sumLen/2
        ①indexa+1+indexb+1 = (sumLen-1)/2 ,说明nums[index+1]与nums2[indexb+1]两个元素较小的那个元素就是最终数组nums3的中位数,结束。
        ②indexa+1+indexb+1 < (sumLen-1)/2，
        
        indexa1=indexa;indexb1=indexb;//记录上次indexa、indexb的值
        回到第二步
        //更新indexa、indexb的值
            if( (indexa+want/2) > (nums1.length-1) ){
                indexb=indexb+want-(nums1.length-1-indexa);
                indexa=nums1.length-1;
            }else if( (indexb+want/2) > (nums2.length-1)){
                indexa=indexa+want-(nums2.length-1-indexb);
                indexb=nums2.length-1;
            }else{
                indexa=indexa+want/2; indexb=indexb+want/2;
            }
        比较nums1[indexa]与nums2[indexb]的大小(谁大谁二分)，
    ②如果sumLen为偶数，判断indexa+1+indexb+1与sumLen/2大小
        ①indexa+1+indexb+1 = sumLen/2,记录nums[indexa]与nums[indexb]中较大的值为c1，记录nums[indexa+1]与nums[indexb+1]中较小的值为c2，最终数组nums3的中位数为(c1+c2)/2，结束。
        ②indexa+1+indexb+1 < sumLen/2，
            indexa1=indexa;indexb1=indexb;//记录上次indexa、indexb的值
            回到第二步

 时间复杂度好像不满足O(log(m+n)),不过这应该是一种可行的求解办法，有错误不足之处欢迎留言批评指正。