三角函数公式，没人比我全【手册】【图文】

       三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

三角函数公式看似很多、很复杂，但只要掌握了三角函数的本质及内部规律，就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。

正弦、余弦和正切的图

这里有些美丽的图……

正弦 的 图

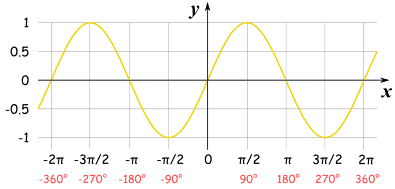
正弦函数的图是美丽的波浪形曲线（每 2π 弧度（360°）重复一遍）。

图从 0 开始，在 π/2 弧度（90°）上升到 1，然后降回 -1。

 

余弦 的 图

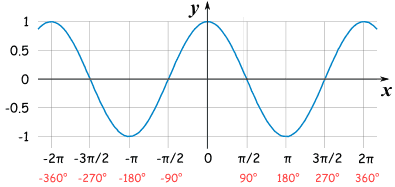
余弦和正弦一样，但图从 1 开始，下降到角的值为 π 弧度 （180°），然后再上升.

 

正弦和余弦的图

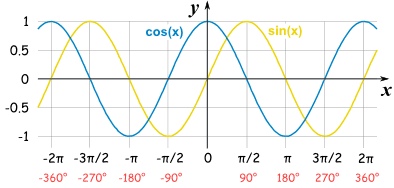
正弦和余弦就像好朋友：一个跟着另一个，隔开的距离是刚好 "π/2" 弧度（90°）。

 

正切函数 的 图

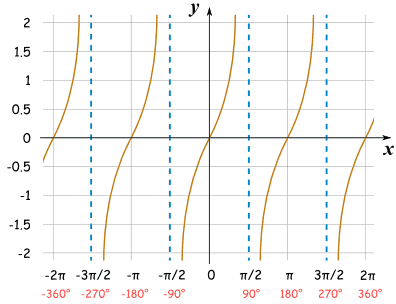
正切的图有完全不同的形状……它处于正与负无穷大之间，每π 弧度（180°）经过 0 一次，像这样：

在π/2 弧度（90°），和 -π/2、3π/2 等等，正切函数是 未定义的，因为它可以是正无穷大 或 负无穷大。

 

反正弦、反余弦和反正切

反正弦、反余弦和反正切的图是：

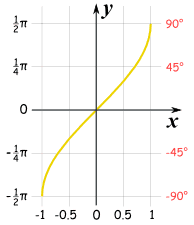
反正弦

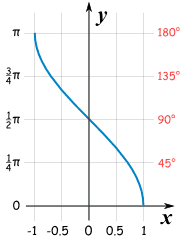
反余弦

 

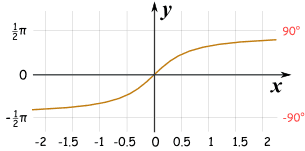
反正切图

 

镜像

这是余弦 和 反余弦 画在同一图上：

余弦和反余弦

它们是沿对角线的镜像！