搞懂标准差和方差

标准差和方差

差的意思是离正常有多远

标准差

标准差是数值分散的测量。

标准差的符号是 σ （希腊语字母 西格马，英语 sigma）

公式很简单：方差的平方根。那么…… "方差是什么？"

方差

方差的定义是：

离平均的平方距离的平均。

按照以下的步骤来计算方差：

• 求数值的 平均
• 从每一个数值减去平均，然后求差的平方。
• 求结果的平均。（为什么要求平方？)

例子

你和朋友们量度了狗狗的身高（毫米）：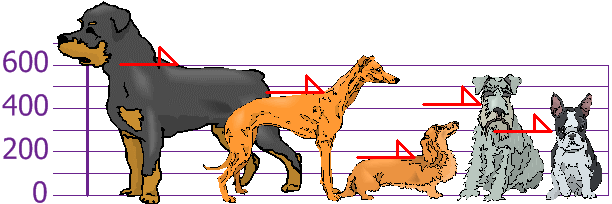

身高（到肩膀）是：600mm、470mm、170mm、430mm 和 300mm。

求平均、方差和标准差。

第一步是求平均：

答案：

平均  =  600 + 470 + 170 + 430 + 3005  =  19705  =  394

平均身高是 394 mm。我们画在图上：

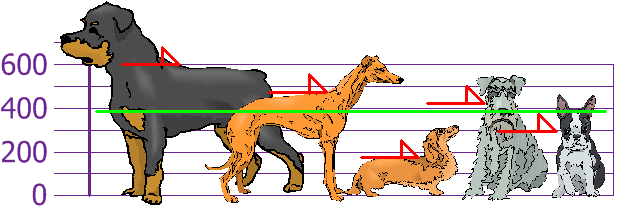
接着求每条狗和平均的距离：

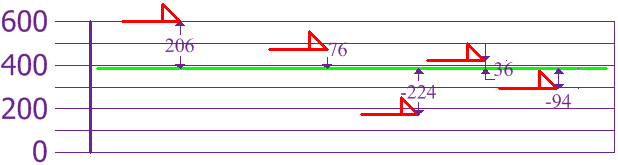
要计算方差，求每个距离的平方，然后求平均：

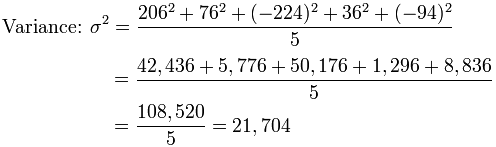
方差是 21,704

标准差是方差的平方根：

标准差
σ	= √21,704
	= 147.32……
	= 147 （到最近的毫米）

 

标准差很有用。 我们现在可以显示哪个高度是在离平均一个标准差（147mm）之内：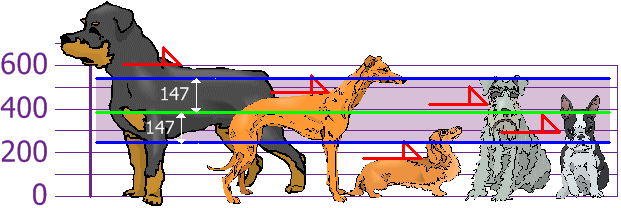

标准差是一个甄别数值是正常与否的"标准"。

罗德维拉犬是高的狗，腊肠犬是矮的狗……但不要告诉它们！

现在去试试 标准差计算器。

可是……如果数据是样本数据

以上例子的数据是对象总体的数据（我们的对象就是那 5条狗）。

但如果数据是个样本（只是对象总体的一部分），计算便会有点改变！

如果你有 "N"个数值，而这些数值是：

• 对象总体：在求方差时除以 N（如上）
• 样本：在求方差时除以 N-1

其他的计算步骤不变，包括计算平均在内。

例子：如果我们的 5条狗只是更多狗里的的一个样本，我们便要除以 4，而不是除以 5：

样本方差 = 108,520 / 4 = 27,130

样本标准差 = √27,130 = 164 （到最近的毫米）

想象这是对样本数据的 "修补"。

公式

这是在 标准差公式 网页里的两个公式（你可以去看看来了解更多）：

"对象总体标准差"：
"样本标准差"：

乍看很复杂，但其实只是在计算样本方差时，有个重要的改变：
以除以 N-1 来代替除以 N。

 

 

*脚注：为什么要求差的平方？

如果我们只把和平均的差加起来……负值和正值便会互相抵消：

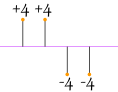4 + 4 − 4 − 44 = 0

这不行。我们可以用绝对值吗？

|4| + |4| + |−4| + |−4|4 = 4 + 4 + 4 + 44 = 4

不错（这叫 平均差），但看看这个例子：

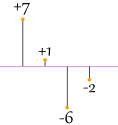|7| + |1| + |−6| + |−2|4 = 7 + 1 + 6 + 24 = 4

糟了！数据比较分散，但结果还是 4。

我们来试试求每个差的平方（最后才取平方根）：

		√(42 + 42 + 42 + 424) = √(644) = 4
		√(72 + 12 + 62 + 224) = √(904) = 4.74...

好极了！当数据比较分散时，标准差也比较大……正是我们想要的。

其实这个方法和 两点之间的距离 都是基于同一个原理，不过应用不同而已。

同时，用代数来处理平方和平方根比处理绝对值要容易很多，标准差也比较容易被应用在其他数学领域。

 

样本标准差的理解：

样本标准差的意义是用于估计总体标准差，你需要理解下面2个内容：

1）当你选择一个样本后，相比总体，你拥有数据的数量是变少了，因此，与总体中的数值偏离平均值的程度相比，样本中很有可能把较为极端的数值排除在外，这样使得数值更有可能以更紧密的方式聚集在均值周围。

也就是说，样本的标准差要小于总体标准差。

深蓝区域是距平均值小于一个标准差之内的数值范围，在正态分布中，此范围所占比率为全部数值之68%；两个标准差之内（深蓝，蓝）的比率合起来为95%；三个标准差之内（深蓝，蓝，浅蓝）的比率合起来为99.7%。

所以，为了更好的用样本估计总体的标准差，统计学家就将标准差的公式做了改造：即原来的标准差公式是除以n，为了用样本估计总体标准差，现在是除以n-1。这样就使得标准差略大。弥补了样本的标准差小于总体标准差的不足。

所以很多书上会直接把除以n-1的标准差叫做样本标准，其实这个样本标准差的目的是用于估计总体标准差。

 

2） 你可能会疑惑，那我什么时候标准差除以n还是n-1呢？

这是由数学推理得出的： 估计量的偏差